
| > | restart:#"m13_p62.mw" |
| > | read`../therm_proc.m`:with(therm_proc): |
Consider a cylindrical evacuated enclosure 50 mm in diameter and 50 mm in length. One of the bases is a thin plate exposed on the outside to the 2.7 K of outer-space background radiation, while all the other surfaces are kept at constant temperature. Find:
a) All the view factors implied.
b) Temperature of the exposed base in the blackbody limit, with 300 K for the temperature-regulated surfaces.
c) Radiation exchange between each pair of surfaces in the above case.
d) Repeat the problem considering now an emissivity =0.5 for all the surfaces.
e) The same, but releasing the fixed temperature condition at the base, which should now be considered thermally insulated.

| > | dat:=D=0.05*m_,L=0.05*m_,Tinf=2.7*K_,Tw=300*K_,epsilon=0.5,Const,SI1,SI2: |
a) All the view factors implied.
View factors for the external surfaces are trivial: F1'4=1. For internal view factors, we look at "Base to lateral surface of a hollow cylinder in Table of view factors,
| > | eqF13:=F13=(sqrt(4*r^2+1)-1)/(2*r^2);r=R/L;r_:=subs(dat,(D/2)/L);F13_:=subs(r=r_,rhs(eqF13));F12=1-F13;F12_:=1-F13_; |
| (1) |
i.e. 83 % of the radiation issuing from the internal face of 1 (emission plus reflections) will imping on surface 3 (the lateral cylindrical surface), and the other 17 % will reach the opposite base 2.
For the reciprocal view factors (F21=F12 by symmetry):
| > | F31=A1*F13/A3;eqA1:=A1=Pi*D^2/4;eqA1_:=subs(dat,%);A2=A1;eqA3:=A3=Pi*D*L;eqA3_:=subs(dat,%);F31_:=rhs(eqA1_)*F13_/rhs(eqA3_);F33=1-2*F31;F33_:=1-2*F31_; |
| (2) |
i.e. 21 % of the exitance of surface 3 goes to base 1, another 21 % goes to base 2, and the remaining 59 % bounces back to surface 3. Of course F11=0 (non-concave surface).
b) Temperature of the exposed base in the blackbody limit, with 300 K for the temperature-regulated surfaces
If all surfaces are blackbodies and T2=T3, the energy balance of the exposed plate at the steady state is:
| > | eqBE:=Qleft_out=Qright_in;eqBE:=A1*sigma*(T1^4-Tinf^4)=A1*sigma*(Tw^4-T1^4);T1_:=fsolve(subs(eqA1_,dat,SI0,%),T1=100..500)*K_;'T1'=TKC(%); |
| (3) |
i.e. plate 1 attains -21 ºC.
c) Radiation exchange between each pair of surfaces in the above case.
We name Qij the net radiation exchanged between i and j although it is not properly heat (it might be non-zero between equal-temperature surfaces of different emissivity, contrary to definition of heat).
| > | Q1p:=A1*sigma*(Tinf^4-T1^4);Q1p_:=subs(T1=T1_,eqA1_,dat,SI1,%);Q1:=A1*sigma*(Tw^4-T1^4);Q1_:=subs(T1=T1_,eqA1_,dat,SI1,%);Q12:=A1*F12*sigma*(Tw^4-T1^4);Q12_:=subs(T1=T1_,eqA1_,F12=F12_,dat,SI1,%);Q13:=A1*F13*sigma*(Tw^4-T1^4);Q13_:=subs(T1=T1_,eqA1_,F13=F13_,dat,SI1,%); |
| (4) |
i.e. plate 1 exchanges with the cold background Q1p=-0.45 W (net loss from surface 1p), the same radiant power absorbed from the inside at surface 1 (0,37 W coming from the lateral wall 3, and 0.08 W coming from the opposite base 2; 0.37+0.08=0.45).
d) Repeat the problem considering now an emissivity =0.5 for all the surfaces.
We use the exitance method. The electrical-equivalent circuit is:
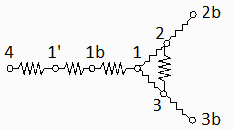
We apply flow continuity at nodes 1b,1,2,3 (we skip node 1' by joining series resistances from 4 to 1b). We have 4 unknowns (M1bb,M1,M2,M3), and the 4 equations are:
| > | eq1b:=epsilon*A1*(M4bb-M1bb)=epsilon*A1*(M1bb-M1)/(1-epsilon);eq1:=epsilon*A1*(M1bb-M1)/(1-epsilon)=A1*F12*(M1-M2)+A1*F13*(M1-M3);eq2:=A1*F12*(M1-M2)+A2*F23*(M3-M2)=(M2-M2bb)/((1-epsilon)/(A2*epsilon));;;eq3:=A1*F13*(M1-M3)+A2*F23*(M2-M3)=(M3-M3bb)/((1-epsilon)/(A3*epsilon));; |
| (5) |
Solving with M2bb=M3bb=sigma*Tw^4:
| > | eq1b_:=subs(M4bb=sigma*Tinf^4,eqA1_,dat,eq1b);eq1_:=subs(M4bb=sigma*Tinf^4,eqA1_,F12=F12_,F13=F13_,dat,eq1);eq2_:=subs(M4bb=sigma*Tinf^4,M2bb=sigma*Tw^4,A2=A1,F12=F12_,F23=F13_,eqA1_,dat,eq2);eq3_:=subs(M3bb=sigma*Tw^4,M4bb=sigma*Tinf^4,A2=A1,F23=F13,eqA1_,eqA3_,F12=F12_,F13=F13_,dat,eq3);sol_:=solve({eq1b_,eq1_,eq2_,eq3_},{M1bb,M1,M2,M3});T1_:=subs(sol_,dat,SI0,(M1bb/sigma)^(1/4))*K_;'T1'=TKC(%);Q1p:=epsilon*A1*(M4bb-M1bb);Q1p_:=subs(sol_,M4bb=sigma*Tinf^4,eqA1_,dat,SI1,Q1p);Q12:=A1*F12*(M1-M2);Q12_:=subs(sol_,eqA1_,F12=F12_,dat,SI1,Q12);Q13:=A1*F13*(M1-M3);Q13_:=subs(sol_,eqA1_,F13=F13_,dat,SI1,Q13);Q23:=A2*F23*(M2-M3);Q23_:=subs(sol_,A2=A1,eqA1_,F23=F13_,dat,SI1,Q23); |
| (6) |
i.e. plate 1 attains T1=-24 ºC. if e=0.5 (it was -21 ºC with e=1) As for the radiation exchanges, now surface 1' exchanges 0.21 W with Tinf (instead of the 0.45 W before), and surface 1 gets Q21=0.04 W from 2 and Q32=0.18 W from 3. Notice that Q23=0.003 W, what contradits the concept of heat transfer since T2 and T3 are equal; the explanation is that we have used here Q not for heat but for the net radiation exchange (heat can only be defined at a unique surface).
e) The same, but releasing the fixed temperature condition at the base, which should now be considered thermally insulated.
Now T2 is unknown, and eq2 changes to a re-radiating condition:
| > | eq1b:=epsilon*A1*(M4bb-M1bb)=epsilon*A1*(M1bb-M1)/(1-epsilon);eq1:=epsilon*A1*(M1bb-M1)/(1-epsilon)=A1*F12*(M1-M2)+A1*F13*(M1-M3);eq2:=A1*F12*(M1-M2)=A2*F23*(M2-M3);eq3:=A1*F13*(M1-M3)+A2*F23*(M2-M3)=(M3-M3bb)/((1-epsilon)/(A3*epsilon));eq1b_:=subs(M4bb=sigma*Tinf^4,eqA1_,dat,eq1b);eq1_:=subs(M4bb=sigma*Tinf^4,eqA1_,F12=F12_,F13=F13_,dat,eq1);eq2_:=subs(M4bb=sigma*Tinf^4,A2=A1,F12=F12_,F23=F13_,eqA1_,dat,eq2);eq3_:=subs(M3bb=sigma*Tw^4,M4bb=sigma*Tinf^4,A2=A1,F23=F13,eqA1_,eqA3_,F12=F12_,F13=F13_,dat,eq3);sol_:=solve({eq1b_,eq1_,eq2_,eq3_},{M1bb,M1,M2,M3});T1_:=subs(sol_,dat,SI0,(M1bb/sigma)^(1/4))*K_;'T1'=TKC(%);T2_:=subs(sol_,dat,SI0,(M2/sigma)^(1/4))*K_;'T2'=TKC(%);Q1p:=epsilon*A1*(M4bb-M1bb);Q1p_:=subs(sol_,M4bb=sigma*Tinf^4,eqA1_,dat,SI1,Q1p);Q12:=A1*F12*(M1-M2);Q12_:=subs(sol_,eqA1_,F12=F12_,dat,SI1,Q12);Q13:=A1*F13*(M1-M3);Q13_:=subs(sol_,eqA1_,F13=F13_,dat,SI1,Q13);Q23:=A2*F23*(M2-M3);Q23_:=subs(sol_,A2=A1,eqA1_,F23=F13_,dat,SI1,Q23); |
| (7) |
i.e. if surface 2 is insulated, plate 1 attains T1=-25 ºC (instead of -24 ºC) and surface 2 equilibrates to T2=19 ºC (292 K instead of the 300 K previously imposed).
The net radiation exchanges are almost the same: 0.21 W to the outside, and 0.03+0.18=0.21 W from the inside, except that now Q23=0.03 W (0.003 W before).
| > |