| > | restart:#"m07_p53" |
En un recipiente rígido de 100 litros hay una mezcla de 4 kg de propano y 12 kg de butano a 500 kPa, estando atemperado en aire ambiente a 100 kPa y 30 ºC. Se pide:
a) Calcular la fracción molar de propano. Hacer un esquema p-x (presión/composición) de las mezclas propano/butano a 30 ºC, e indicar en él los valores de las presiones extremas, y las de ebullición y condensación de la mezcla dada.
b) Calcular la composición de cada fase a 30 ºC y 500 kPa, indicando en un diagrama T-x a 500 kPa sus estados, así como la fracción molar de fase gaseosa.
c) Calcular el volumen de líquido en esas condiciones.
d) Se quiere determinar el estado termodinámico que alcanzaría un pequeño escape de líquido a través de una válvula, si éste fuese rápido y hasta la presión ambiente. Hacer un esquema del proceso en un diagrama p-h. Calcular la temperatura de salida suponiendo que, en vez de la mezcla líquida, lo que escapa fuese butano líquido puro.
Datos:
| > | read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):Digits:=5: |
| > | su1:="C3H8":su2:="C4H10":dat:=[V=0.1*m_^3,m1=4*kg_,m2=12*kg_,p0=100e3*Pa_,T0=(30+273.15)*K_,p1=500e3*Pa_]; |
Datos de sustancias puras obtenidos de Gas_table y de Liq_table; presión de vapor por Antoine.
1=Propano, 2=Butano.
| > | g1dat:=get_gas_data(su1):l1dat:=get_liq_data(su1);g2dat:=get_gas_data(su2):l2dat:=get_liq_data(su2);dat1:=op(dat),g1dat,l1dat,Const,SI2,SI1:dat2:=op(dat),g2dat,l2dat,Const,SI2,SI1:pv1:=proc(T) global su1;get_pv_data(su1);RETURN(pv(T)):end:pv2:=proc(T) global su1;get_pv_data(su2);RETURN(pv(T)):end: |
| (1) |
Modelo de mezcla binaria bifásica ideal (ley de Raoult):
| > | eqNV:=xv1+xv2=1;eqNL:=xl1+xl2=1;eqC1:=xv1*xv0+xl1*xl0=x01;eqC2:=xv2*xv0+xl2*xl0=x02;eqE1:=xv1/xl1=pv1/p;eqE2:=xv2/xl2=pv2/p;sol1:=solve({eqNV,eqNL,eqE1,eqE2},{xv1,xv2,xl1,xl2});sol2:=solve({eqC1,eqC2},{xv0,xl0}); |
| (2) |
a) Calcular la fracción molar de propano. Hacer un esquema p-x (presión/composición) de las mezclas propano/butano a 30 ºC, e indicar en él los valores de las presiones extremas, y las de ebullición y condensación de la mezcla dada.
La línea de ebullición en el diagrama p-x para mezclas ideales es una recta.
| > | y1=m1/(m1+m2);y1_:=evalf(subs(dat,m1/(m1+m2)));x1=(y1/M1)/(y1/M1+y2/M2);x1_:=subs(M1=M,dat1,M2=M,dat2,(y1_/M1)/(y1_/M1+(1-y1_)/M2));pboil='x1*pv1(T0)+x2*pv2(T0)';pv1_:=evalf(subs(dat,pv1(T0)));pv2_:=evalf(subs(dat,pv2(T0)));pboil_:=x1_*pv1_+(1-x1_)*pv2_;eqs_cond:=[subs(xv1=x1_,pv1=pv1_,eqE1),subs(xv2=1-x1_,pv2=pv2_,xl2=1-xl1,eqE2)];sol_:=op(solve(%,[p,xl1]));pcond_:=subs(%,p);ntot:=m1/M1+m2/M2;ntot_:=subs(M1=M,dat1,M2=M,dat2,dat,%); |
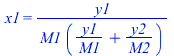 |
|
| (3) |
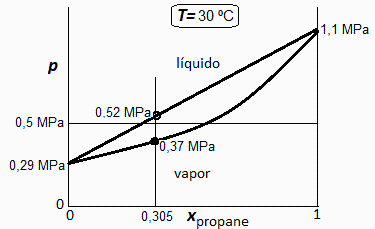
i.e. con el modelo de mezcla ideal, a 30 ºC solo puede haber mezclas bifásicas propano/butano si 0,29<p/MPa<1,1, y, para las mezlas con xpro=0,31 solo si 0,37<p/MPa<0,52, así que para p=0,5 MPa será bifásica. Hay 4+12=16 kg en total, que son 298 mol en total (4/0,044=91 mol de propano más 12/0,058=207 mol de butano); la fracción másica global de propano es del y1=4/(4+12)=25 %, la molar global es del x1=31 %.
b) Calcular la composición de cada fase a 30 ºC y 500 kPa, indicando en un diagrama T-x sus estados, así como la fracción molar de fase gaseosa.
Substituyendo en las ecuaciones del MMI:
| > | sol1_:=subs(p=p1,pv1=pv1_,pv2=pv2_,dat,sol1);sol2_:=subs(sol1_,x01=x1_,x02=1-x1_,sol2); |
| (4) |
i.e. en la fase líquida hay 27 % molar de propano (y 73 % de butano), y en la fase gaseosa hay 59 % molar de propano (y 41 % de butano). Un xv0=10 % del total de moles está en fase gaseosa (el otro 90 % en fase líquida). Los estados en el diagrama T-x son:
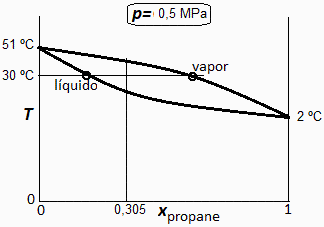
c) Calcular el volumen de líquido en esas condiciones.
Para saber el volumen de líquido hay que calcular su densidad (lo haremos para ambas fases). Una primera estimación sería suponer que los 16 kg son de butano líquido, con lo que Vliq=16/600=27 litros.
| > | Mmv:=xv1*M1+xv2*M2;Mmv_:=subs(sol1_,M1=M,dat1,M2=M,dat2,%);Mml:=xl1*M1+xl2*M2;Mml_:=subs(sol1_,M1=M,dat1,M2=M,dat2,%);eqETvap:=rho=p*Mm/(R[u]*T);eqETvap_:=rho=subs(Const,dat,SI2,p1*Mmv_/(R[u]*T0));eqETliq:=1/rho=yl1/rho1+yl2/rho2;eqETliq:=rho=1/(xl1/rho1+xl2/rho2);eqETliq_:=rho=subs(sol1_,rho1=rho,dat1,rho2=rho,dat2,rhs(%));yl0:='xl0*Mml/(xv0*Mmv+xl0*Mml)';yl0_:=subs(sol1_,sol2_,M1=M,dat1,M2=M,dat2,%);yv0_:=1-yl0_;mliq:=mtot*'yl0';mliq_:=subs(dat,(m1+m2)*yl0_);Vliq:='mliq'/rholiq;Vliq_:=subs(dat,mliq_/rhs(eqETliq_));mvap:='ntot*xv0*Mmv';mvap_:=subs(sol2_,dat,ntot_*xv0*Mmv_);Vvap_:=subs(sol2_,dat,ntot_*xv0*Mmv_/rhs(eqETvap_)); |
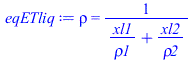 |
|
| (5) |
i.e. la fase líquida ocupa unos 24 litros (mliq=14,5 kg), pero la fase gaseosa ocuparía unos 143 litros (1,5 kg), i.e. 167 L en total, lo que no concuerda en absoluto con el dato del enunciado (Vtot=100 L).
Podría pensarse que el sistema esta sobredeterminado porque se dan T, p, y v (30 ºC, 500 kPa, v=Vtot/mtot=0,1/16), y solo hay dos variables independientes como enseña la regla de las fases, V=2+C-F=2+2-2=2, pero resulta que no hemos hecho uso del dato de la v (solo de la relación de masas), por lo que cabe concluir que esta enorme diferencia en volúmenes podría deberse al modelo de mezcla ideal.
Para aclarar esta inconsistencia, se presentan los resultados más precisos del NIST para una mezcla de 4 kg de propano y 12 kg de butano (x01=0,250, y01=0,305) a 30 ºC y 500 kPa) para calcular el volumen real. Según el NIST:
-Las fracciones molares de propano en cada fase son xv1=0,573 y xl1=0,297 (y no xv1=0,59 y xl1=0,27 como daba el modelo de mezcla ideal). La desviación no parece muy importante.
-La fracción másica de vapor es yv0=0,0266 (y no yv0=0,093 que hemos calculao) , i.e. hay 16·0,0266=0,426 kg de vapor y 16-0,426=15,6 kg de líquido (y no 1,5 kg de vapor y 14,5 kg de líquido que habíamos alculado). Esta gran discrepancia en el valor de la fracción másica de vapor, que realmente es yv0=0,0266 y no la yv0=0,93 calculada, y que se debe a errores no muy grandes en los valores aquí usados de las densidades líquidas (pero que se amplifican mucho), explica la enorme discrepancia en volúmenes de gas (de 0,4 kg a 1,5 kg el error relativo es enorme, mientras que para la fase líquida apenas importa que haya 15,6 kg o 14,5 kg; la diferencia es solo del 7 %).
-Las densidades de cada fases son rhovap=11,2 kg/m3 (en vez de 10,4 kg/m3), y rholiq=574 kg/m3 (en vez de 596 kg/m3), pero la densidad media real es rhotot=240 kg/m3 y no los (16/(0,167)=96 kg/m3 que da el modelo de mezcla ideal, ni los 16/0,1=160 kg/m3 que indica el enunciado.
Si admitimos que todos los datos del enunciado son fidedignos, la única explicación de la discrepancia entre la densidad media dada (16/0,1=160 kg/m3) y la densidad media real para esa T, p, y composición (los 240 kg/m3 del NIST), es la incertidumbre en los datos; de todas ellas la de mayor relevancia es la temperatura, como se ve al introducir un pequeño cambio.
Una mezcla de 4 kg de propano (puro) más 12 kg de butano (puro), con los datos del NIST tiene:
-a 30 ºC y 0,5 MPa tiene una fracción másica de vapor es yv0=0,0267, y habría 16·0,0267=0,426 kg de vapor y 16-0,426=15,5 kg de líquido; la densidad media es 240 kg/m3, y el Vtot=16/240=67 L, pero
-a 30,5 ºC y 0,5 MPa ya tiene una fracción másica de vapor es yv0=0,0564, y habría 16·0,0564=0,902 kg de vapor y 16-0,902=15,1 kg de líquido; la densidad media es 147,6 kg/m3, y el Vtot=16/147,6=108 L. El volumen de líquido sería pues Vliq=mliq/rholiq=15,2/547=0,027 m3, i.e. 27 L en lugar de los 24 L que hemos deducido con el MMI (casualmente coincidente con la primera estimación).
También podríamos haber calculado el volumen de líquido por otros procedimientos, e.g.:
Método3. Calcular la masa de líquido a partir de la masa total y la masa de la fase gaseosa suponiendo esta que ocupa todo el volumen (lo que dará un límite), y hacer uso de las densidades calculados:
| > | mliq__:=mtot-mvapVtot;mliq__:=m1+m2-rho_vap*Vtot;mliq__:=subs(eqETvap_,dat,m1+m2-rho*V);Vliq__:='mliq'/rho_liq;Vliq__:=mliq__/rhs(eqETliq_); |
| (6) |
Método 4. Como sabemos que xL=0,90 y sabemos las masas molares de líquido y la total, MmL y Mm, podemos calcular la masa de líquido de yL=mL/mT=(nL*MmL)/(nT*MT), y luego VL=mL/rhoL.
| > | yL:=(nL*MmL)/('ntot'*Mtot);yL_:=subs(sol2_,M1=M,dat1,M2=M,dat2,dat,xl0*ntot_*Mml_/(ntot_*(x1_*M1+(1-x1_)*M2)));mliq__:='yL'*(m1+m2);mliq__:=subs(dat,yL_*(m1+m2));Vliq__:=mliq__/rhs(eqETliq_); |
| (7) |
i.e. con cualquiera de estos métodos se obtiene un valor bastante aproximado:26 L con el método 3, 25 L con el método 4..
d) Se quiere determinar el estado termodinámico que alcanzaría un pequeño escape de líquido a través de una válvula, si éste fuese rápido y hasta la presión ambiente. Hacer un esquema del proceso en un diagrama p-h. Calcular la temperatura de salida suponiendo que, en vez de la mezcla líquida, lo que se escapa fuese butano puro.
Se trata de un proceso de expansión isentálpica en la válvula (de 1 a 2 en la fugura), entrando líquido saturado (i.e. una mezcla monofásica con 27 % de propano, a 500 kPa y 30 ºC), y saliendo una mezcla bifásica a 100 kPa y una temperatura y composición que cumpla el balance energético (Dh=0), los balances másicos (Dn1=0, Dn2=0), y el equilibrio de fases. El cálculo es complejo y conviene tomar un valor de T2 e ir iterando hasta conseguir Dh=0.

Si la expansión fuera con butano puro líquido saturado a 30 ºC (da igual si es a 500 kPa o no, con tal de que sea pv2>286 kPa para que sea líquido), solo queda el balance energético y el equilibrio de fases, que aquí se reduce a la Ec. de Clapeyron o la de Antoine.
Tomando como origen h=0 para el líquido en el punto triple:
| > | p2:=p0;eqEF:=p[v](T[2])=p[1];T2_:=solve(subs(dat,pv2(T)=p2),T);'T2_'=TKC(%);eqBE:=h1=(1-x)*h2liq+x*h2vap;hliq:=subs(dat,hl(T));h1_:=subs(dat1,T=T0,dat,hl(T));h2liq_:=subs(dat1,T=T2_,hl(T));h2vap_:=subs(dat1,T=T2_,SI2,hv(T));x_:=(h1_-h2liq_)/(h2vap_-h2liq_); |
| (8) |
i.e. saldría un flujo bifásico a -0,8 ºC, con una fracción másica de vapor del 16 %.
ADICIONAL
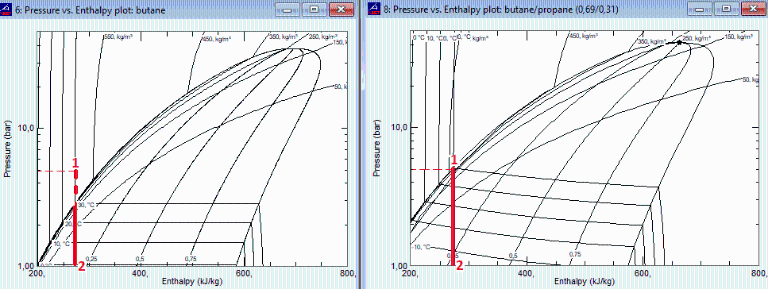
Con los datos del NIST se han dibujado los diagramas p-h de la expansión en la válvula para el caso de butano puro, y para el caso de la mezcla original. Se puede ver que al expandir butano puro desde 500 kPa y 30 ºC hasta 100 kPa sale a -0,5 ºC (en vezz de -0,8 ºC) y con una fracción másica de vapor del 19 % (en vez de nuestro valor x=16 % con el modelo de sustancia perfecta).
Si en lugar de butano puro entra la mezcla líquida con 69 % de butano molar (x1=0,305), saldría a -15 ºC con x=26 %.
| > |