Tomamos los datos termoópticos de la Tabla. Sea 'b'=blanca, 'm'=metalizada, 'p'=planeta.

>	dat:=[Rgeo=42100e3*m_,Rp=6378e3*m_,Tp=288.15*K_,epsilon[p]=0.615,rho[p]=0.3,R=0.1*m_,E=1360*W_/m_^2,Tinf=2.7*K_,alpha[b]=0.2,epsilon[b]=0.85,epsilon[m]=0.05,H=0.1*m_];dat:=op(dat),Const,SI2,SI1:h:='h':assume(h>1)

(1)

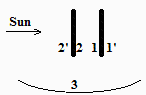
a) Plantear su balance térmico en un caso general, iluminado por el Sol, pero despreciando el acoplamiento con el resto del satélite. Estimar la posible contribución terrestre.

Los datos de albedo y emisión terrestres los tomamos de la "Properties of planets and their moons".

Los datos de propiedades superficiales de los materiales los tomamos de la Tabla 2 de "Thermo-optical properties".

La radiadión recibida de la Tierra se podrá despreciar porque la absorción por albedo máxima sería Qa=9,4 W/m2 si fuera una superficie negra frontal al punto subsolar, y por IR sería Qp<5,5 W/m2, como vamos a calcular, mientras que la irradiancia solar es 1360 W/m2 (+/50 W/m2 en los solsticios).

También podríamos considerar térmicamente aislada la cara aluminizada, por ser eps<<1.

Sea A el área de una cara del disco. El balance energético térmico es:

>

eqBE:=C*dT/dt=Wdis+Qnet;eqBE:=C*dT/dt=Wdis+Qs+Qa+Qp-Qinf;eqBE:=C*dT/dt=Wdis+Qs-Qinf;eqBE:=C*dT/dt=Wdis+alpha[b]*E*A*cos(beta)-A*(epsilon[b]+epsilon[m])*sigma*T^4;eqh:=h=Rgeo/Rp;eqh_:=subs(dat,%);F12_0:=1/h^2;F12_0_:=subs(eqh_,%);Qp_max:=epsilon[p]*sigma*Tp^4*'F12_0';Qp_max_:=subs(eqh,dat,%);Qa_max:=rho[p]*E*'F12_0';Qa_max_:=subs(eqh,dat,%);

	(2)

F12_0=0,023 significa que tan solo el 2,3 % de lo que emita o refleje la Tierra puede llegar a incidir en una placa frontal en órbita geoestacionaria.

Qp_max=5,5 W significa que como máximo se absorberían 5,5 W en el IR (si fuese un disco negro mirando a la Tierra; 5,5·0,85=4,7 W/m2 para la cara blanca).  La absorción IR es uniforme en todo la órbita para una actitud del satélite y una emitancia planetaria fijas, pero no se dice cuál es la actitud del disco respecto a Tierra. En nuestro caso, este valor se reduciría al multiplicarlo por la inclinación del disco respecto al nadir, cos(beta), y por la absortancia IR (0,85 si es la cara blanca la del nadir, o 0,05 si es la metalizada). Como se ve, es despreciable frente a la irradiancia solar.

Qa_max=9,4 W significa que como máximo se absorberían 9,4 W por reflexión solar planetaria (albedo), que correspondería a un disco negro cuando coinciden el punto subsolar y el punto subsatélite, pero este valor, aparte de reducirse con la absortancia solar del disco (alpha[b] o alpha[m]) y con su inclinación respecto al nadir (cos(beta)), se reduce rápidamente con el ángulo de la posición orbital respecto al punto subsolar (cos(theta)); para la cara blanca, que es la que más absorbe de las dos, sería 9,4·0,2=1,9 W/m2.

b) Temperatura que alcanzaría el disco en régimen estacionario.

>	eqBE:=0=Qs-Qinf;eqBE:=0=alpha[b]*E*A-A*(epsilon[b]+epsilon[m])*sigma*T^4;eqA:=A=Pi*R^2;eqA_:=evalf(subs(dat,%));eqBE_:=subs(eqA_,dat,SI0,eqBE);T_:=fsolve(%,T=10..1000)*K_;'T_'=TKC(%);

	(3)

i.e. el disco quedaría a 270 K (-3 ºC); si se hubiera considerado aislado por detrás, quedaría a 274 K (1 ºC).

c) Plantear los balances térmicos si se dispone delante del disco antedicho otro disco igual, pintado de negro por las dos caras, separado 0,1 m del anterior, y calcular las temperaturas estacionarias.
Habría que recurrir al método de las exitancias, pero una buena aproxinmación es considerar que el disco original también es un cuerpo negro (la superficie delantera), porque como casi no radia hacia atrás, la exitancia hacia delante (i.e. la reflexión IR sumada a la emisión propia), casi coincidirá con la emitancia de cuerpo negro. Con este planteamiento:  

>

eqBE1:=C1*dT1/dt=Wdis1+Q21-Q1inf;eqBE2:=C2*dT2/dt=Wdis2+Qs-Q21-Q2inf;eqQ21N:=Q21=A*F12*sigma*(T2^4-T1^4);eqBE1:=0=Q21-A*sigma*T1^4*F13;eqBE2:=0=E*A-Q21-A*sigma*T2^4*(1+F23);eqF12:=F12=1+1/(2*r^2)*(1-sqrt(4*r^2+1));eqr:=r=R/H;eqr_:=subs(dat,%);eqF12_:=subs(eqr_,eqF12);eqF13:=F13=1-F12;eqF13_:=subs(eqF12_,%);eqBE1_:=subs(eqQ21N,eqF12_,eqF13_,eqA_,dat,SI0,eqBE1);eqBE2_:=subs(F23=F13,eqQ21N,eqF12_,eqF13_,eqA_,dat,SI0,eqBE2);sol_:=fsolve({eqBE1_,eqBE2_},{T1,T2},T2=100..1000);T1_:=subs(sol_,T1*K_);'T1_'=TKC(%);T2_:=subs(sol_,T2*K_);'T2_'=TKC(%);Q21_:=subs(eqA_,eqF12_,sol_,dat,SI0,rhs(eqQ21N))*W_;

	(4)

i.e. el disco original quedaría a T1=265 K (-8 ºC) y el delantero a T2=337 K (64 ºC). El calor que pasa del 2 al 1 es Q21=5,4 W. El factor de vista F12=0,38 significa que el 38 % de la radiación que sale de la cara 2 (la cara trasera del disco delantero), incide sobre el disco original.

d) Repetir el punto anterior pero con ambas caras del nuevo disco pintadas de blanco.

Ya no puede ponerse Q21 en la forma anterior dependiente solo de las dos temperaturas, y hay que recurrir al método de las exitancias, cuyo planteamiento es el siguiente.

>	eq1:=(M1-M1bb)/((1-epsilon1)/(A1*epsilon1))=A1*F12*(M2-M1)+A1*F13*(M3-M1);eq2:=(M2-M2bb)/((1-epsilon2)/(A2*epsilon2))=A2*F21*(M1-M2)+A2*F23*(M3-M2);eq3:=(M1-M1bb)/((1-epsilon1)/(A1*epsilon1))=epsilon0*A1*M1bb;eq4:=(M2-M2bb)/((1-epsilon2)/(A2*epsilon2))=-alpha2*E*A2+epsilon2*A2*M2bb;M3:=0

	(5)

Las ecuaciones 1 y 2 son las de balance neto de radiación recibida por la cara 1 y por la cara 2 (las enfrentadas).

La eq3 es el balance de la cara 1 con la 1'. Para la emisividad de 1' ponemos epsilon0 para poder cambiarla luego. Nótese que si epsilon0=0, i.e. si el disco 1 está aislado por detrás, entonces M1=M1bb (entre lo que emite y lo que refleja sale como si emitiera un cuerpo negro), como se ha dicho antes.

La eq4 es el balance de la cara 2 con la 2', i.e. la radiación que llega a la 2 (desde 1 y 3) ha de igualar a la que sale por 2' (hacia 3 menos la aportación solar; se ha tomado alpha2'=alpha2).

Como siempre despreciamos la emitancia de fondo (M3) a 2,7 K.

Son 4 ecuaciones con 4 incógnitas: M1,M1bb,M2,M2bb.

Para el caso de caras 1', 1, y 2 blancas, y 2' metalizada::

>

datBR:=alpha2=alpha[b],epsilon2=epsilon[b],epsilon1=epsilon[b],epsilon0=epsilon[m];sol_:=solve(subs(datBR,A1=A,A2=A,eqA_,F21=F12,eqF12_,F23=F13,eqF13_,dat,SI0,{eq1,eq2,eq3,eq4}),{M1,M1bb,M2,M2bb});T1_:=evalf(subs(sol_,dat,SI0,(M1bb/sigma)^(1/4)))*K_;'T1_'=TKC(%);T2_:=evalf(subs(sol_,dat,SI0,(M2bb/sigma)^(1/4)))*K_;'T2_'=TKC(%);Q21_:=subs(eqA_,eqF12_,T1=T1_,T2=T2_,dat,SI0,rhs(eqQ21N))*W_;

	(6)

i.e. la placa 1 queda a -98 ºC y la 2 a -39 ºC, transmitiéndose solo 1,4 W entre ellas (nótese que, aunque le llamamos Q, no es calor sino intercambio radiativo neto; podría ser distinto de cero con T1=T2 si las emisividades fuesen distintas). Como este resultado para disco blanco se aleja tanto del anterior para disco negro, vamos a comprobar este modelo aplicándoselo a los datos de discos negros:

>

datNN:=alpha2=1,epsilon2=1-1e-6,epsilon1=1-1e-6,epsilon0=0;sol_:=solve(subs(datNN,A1=A,A2=A,eqA_,F21=F12,eqF12_,F23=F13,eqF13_,dat,SI0,{eq1,eq2,eq3,eq4}),{M1,M1bb,M2,M2bb});T1_:=evalf(subs(sol_,dat,SI0,(M1bb/sigma)^(1/4)))*K_;'T1_'=TKC(%);T2_:=evalf(subs(sol_,dat,SI0,(M2bb/sigma)^(1/4)))*K_;'T2_'=TKC(%);Q21_:=subs(eqA_,eqF12_,T1=T1_,T2=T2_,dat,SI0,rhs(eqQ21N))*W_;

	(7)

Exacto. Y ya puestos vamos a resolver correctamente el caso de disco frontal negro con disco trasero original:

>

datNR:=alpha2=1,epsilon2=1-1e-6,epsilon1=epsilon[b],epsilon0=epsilon[m];sol_:=solve(subs(datNR,A1=A,A2=A,eqA_,F21=F12,eqF12_,F23=F13,eqF13_,dat,SI0,{eq1,eq2,eq3,eq4}),{M1,M1bb,M2,M2bb});T1_:=evalf(subs(sol_,dat,SI0,(M1bb/sigma)^(1/4)))*K_;'T1_'=TKC(%);T2_:=evalf(subs(sol_,dat,SI0,(M2bb/sigma)^(1/4)))*K_;'T2_'=TKC(%);Q21_:=subs(eqA_,eqF12_,T1=T1_,T2=T2_,dat,SI0,rhs(eqQ21N))*W_;

	(8)

i.e. vemos la bondad de la aproximación del apartado anterior: el disco original queda a T1=-12 ºC (y no a -8 ºC), el escudo negro apenas varía sus 64 ºC (queda 0,3 K más frío), y el calor intercambiado es de 5,6 W en lugar de 5,4 W.

Otra manera de plantear las ecuaciones sería estableciendo el balance de flujos en los nodos de la analogía eléctrica que se muestra en la figura, que en este caso serían 6 ecuaciones con las 6 incógnitas: M2p,M2bb,M2,M1,M1bb,M1p (que si se eliminan M2p y M1p se reducen a las 4 anteriores (eq1,eq2,eq3,eq4).

>

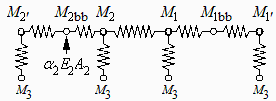
eq_2p:=A2p*F2p3*(M3-M2p)=epsilon2p*A2p*(M2p-M2bb)/(1-epsilon2p);eq_2bb:=epsilon2p*A2p*(M2p-M2bb)/(1-epsilon2p)+alpha2p*A2p*E2p=epsilon2*A2*(M2bb-M2)/(1-epsilon2);eq_2:=epsilon2*A2*(M2bb-M2)/(1-epsilon2)+A2*F23*(M3-M2)=A2*F21*(M2-M1);eq_1:=A2*F21*(M2-M1)+A2*F23*(M3-M2)=epsilon1*A1*(M1bb-M1)/(1-epsilon1);eq_1bb:=epsilon1*A1*(M1bb-M1)/(1-epsilon1)=epsilon1p*A1p*(M1p-M1bb)/(1-epsilon1p);eq_1p:=epsilon1p*A1p*(M1p-M1bb)/(1-epsilon1p)=A1p*F1p3*(M1p-M3);

	(9)

>