| > | restart:#"m13_p58.mw" |
| > | read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):with(plots):with(RealDomain): |
Se requiere un análisis térmico de una placa plana delgada, cuadrada y de 0,1 m de lado, que es un apéndice en un satélite geoestacionario. Se pide:
a) Plantear su balance térmico en un caso general, iluminado por el Sol, pero despreciando el acoplamiento con el resto del satélite. Estimar la posible contribución terrestre.
b) Potencia eléctrica requerida para que la placa no se enfríe por debajo de 50 ºC, en función de la inclinación solar, en los casos en que ambas superficies sean negras o que sean blancas.
c) Potencia eléctrica requerida para mantener la placa a 50 ºC con Sol frontal, en función de la relación /, suponiendo que la cara posterior está aislada con una MLI.
d) Temperatura que alcanzaría la placa pintada de blanco por delante y aislada por atrás, enfrentada al Sol (sin disipación).
e) Plantear los balances térmicos si se dispone delante de la placa antedicha otra placa igual, toda pintada de negro, separada 10 mm de la anterior, y calcular las temperaturas estacionarias.
f) Repetir el punto anterior pero con todas las caras pintadas de blanco.
dat:=[L=0.1*m_,E=1360*W_/m_^2,Tmin=(50+273.15)*K_,Tinf=2.7*K_,alpha=0.2,epsilon=0.85,H=0.01*m_];dat:=op(dat),Const,SI2,SI1:h:='h':assume(h>1)
| (1) |
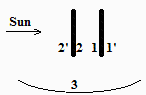
a) Plantear su balance térmico en un caso general, iluminado por el Sol, pero despreciando el acoplamiento con el resto del satélite. Estimar la posible contribución terrestre.
| > | eqBE:=C*dT/dt=Wdis+Qnet;eqBE:=C*dT/dt=Wdis+Qs+Qa+Qp-Qinf;eqBE:=C*dT/dt=Wdis+Qs-Qinf;eqBE:=C*dT/dt=Wdis+alpha*E*A*cos(beta)-2*A*epsilon*sigma*T^4; |
| (2) |
La radiadión recibida de la Tierra también se podrá despreciar porque el albedo Qa es siempre <10 W/m2 y la Qp IR es siempre <5,5 W. El máximo será para placa frontal orientada al punto subsolar. Para el factor de vista tomamos Patch to sphere.
| > | eqh:=h=RGEO/RE;eqh:=h=evalf(42100/6380);F12_0:=1/h^2;F12_0_:=subs(eqh,%);Ep_0:=epsilon*sigma*TE^4*'F12_0';Ep_0_:=subs(epsilon=0.615,TE=288*K_,eqh,dat,%);Ea_0:=rho*E*'F12_0';Ea_0_:=subs(rho=0.3,eqh,dat,%); |
| (3) |
i.e. tan solo el 2,3 % de lo que emita o refleje la Tierra llega a incidir en una placa frontal en órbita geoestacionaria, y no toda se absorberá, si no es cuerpo negro; en el límite de placa negra mirando al punto subsolar en el nadir, Qa/A=9,4 W/m2 y Qp/A=5,5 W/m2.
b) Calcular la potencia eléctrica requerida para que la placa no se enfríe por debajo de 50 ºC, en función de la inclinación solar, en los casos en que ambas superficies sean negras o que sean blancas.
Sea BB el límite de placa negra (blackbody), y WP la placa blance (white plate). Sea beta el ángulo que forma el Sol con la normal. En régimen estacionario:
| > | Wdis:=2*A*epsilon*sigma*Tmin^4-alpha*E*A*cos(beta);WdisBB:=subs(alpha=1,epsilon=1,%);WdisBB_:=subs(A=L^2,dat,%);WdisBBmin:=subs(dat,evalf(subs(beta=0,dat,%)));WdisWP_:=subs(A=L^2,dat,Wdis);WdisWPmin:=subs(dat,evalf(subs(beta=0,dat,%)));plot(subs(SI0,[WdisBB_,WdisWP_]),beta=0..Pi/2,Wdot=-5..15); |
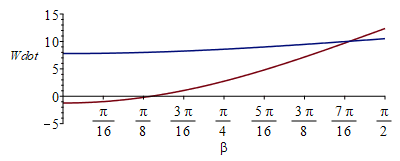 |
i.e. si la placa está de canto (no soleada, beta=90º), hay que compensar toda la emisión propia de la placa, WdisBBmax=12,4 W si es negra (blackbody limit) y 10,5 W si es blanca (se ha tomado propiedades de la Tabla), mientras que si está enfrentada al Sol (beta=0), solo habrá que calentar eléctricamente con WdisWPmin=7,8 W si es blanca, y evacuar 1,2 W si es negra (pero como es dificil refrigerar, cabe concluir que no se puede mantener una placa negra a <50 ºC enfrentada al Sol, se calentaría más).
Nota. Suele suponerse, como aquí, que la radiación solar es unidireccional, pero el tamaño finito del disco solar influiría algo (unos 10^-6 W/m2).
c) Calcular la potencia eléctrica requerida para mantener la placa a 50 ºC con Sol frontal, en función de la relación /, suponiendo que la cara posterior está aislada con una MLI.
| > | Wdis:='Wdis':eqBE:=C*dT/dt=Wdis+alpha*E*A*cos(beta)-A*epsilon*sigma*T^4;Wdis:=A*epsilon*sigma*Tmin^4-alpha*E*A*cos(beta);Wdis_:=evalf(subs(alpha=a_e,epsilon=1,A=L^2,beta=0,dat,%));a_e_Wdis0:=subs(Wdis_=0,dat,solve(%,a_e));semilogplot(subs(SI0,Wdis_),a_e=0.1..10,'Wdis'=-120..10); |
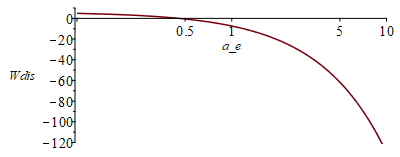 |
i.e. si la relación alpha/epsilon es a/e>0,45 entonces la placa (aislada por atrás) se calentaría por encima de 50 ºC y habría que refrigerar. Si es a/e<0,45 sí que habrá que calentar, como se ha visto para la pintura blanca con a/e=0,20/0,85=0,24.
d) Temperatura que alcanzaría la placa pintada de blanco por delante y aislada por atrás, enfrentada al Sol (sin disipación).
| > | eqBE:=C*dT/dt=Wdis+alpha*E*A*cos(beta)-A*epsilon*sigma*T^4;eqBE:=0=0+alpha*E*A-A*epsilon*sigma*T^4;T_:=max(fsolve(subs(A=L^2,dat,SI0,%),T))*K_;'T_'=TKC(%);Qs=alpha*E*A;subs(A=L^2,dat,%); |
| (4) |
i.e. si a/e=0,20/0,85=0,24, la placa alcanzaría 1 ºC, absorbiendo 2,7 W del Sol y emitiendo 2,7 W al vacío.
e) Plantear los balances térmicos si se dispone delante de la placa antedicha otra placa igual, toda pintada de negro, separada 10 mm de la anterior, y calcular las temperaturas estacionarias.
Sea (1) la cara frontal de la placa original, (2) la cara no iluminada de la placa delantera, y (2') la cara iluminada.
| > | eqBE1:=C1*dT1/dt=Wdis1+Q21-Q1inf;eqBE2:=C2*dT2/dt=Wdis2+Qs-Q21-Q2inf;eqBE1:=0=Q21-epsilon1*A1*sigma*T1^4*F13;eqBE2:=0=alpha2*E*A2-Q21-epsilon2*A2*sigma*T2^4*(1+F23); |
| (5) |
Hay que calcular F12 con la fórmula de la Tabla con w=L/H=10. Como la fórmula es complicada, comprobaremos el resultado con el de discos iguales de radio L/2 (en vez de placas cuadradas).

| > | F12:=(ln(x^4/(1+2*w^2))+4*w*(x*arctan(w/x)-arctan(w)))/(Pi*w^2);x := sqrt(1+w^2);eqw:=w=L/H;eqw_:=subs(dat,%);F12_:=evalf(subs(eqw_,F12));F13_:=1-F12_;F12discs:=1+1/(2*r^2)*(1-sqrt(4*r^2+1));F12discs_:=subs(r=L/(2*H),dat,%);; |
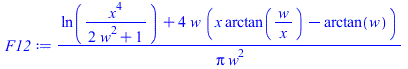 |
|
| (6) |
ok, el 83 % de lo que sale de 1 incide en 2 y el otro 17 % al espacio vacío profundo. El calor intercambiado entre 1 y 2 tiene una expresión sencilla si todas las superficies fuesen cuerpos negros (la aproximación de la placa blanca posterior por placa negra no es mala porque al no estar expuesta al Sol, solo importa la epsilon, que es casi la unidad). Cuando hay, como aquí, solo una superficie gris (eps<1), pero está aislada, el calor intercambiado entre 1 y 2 es el mismo que si fuese eps=1 porque, aunque solo emite eps*M1bb, el resto es lo que refleja de lo que le envía 1.
Con el modelo Black & Black:
| > | F12:='F12':eq12_BB:=Q21=A1*F12*(M2bb-M1bb);eq12_BB:=Q21=sigma*A1*F12*(T2^4-T1^4);eqBE1_:=subs(eq12_BB,F12=F12_,F13=F13_,A1=L^2,epsilon1=1,dat,SI0,eqBE1);eqBE2_:=subs(eq12_BB,F12=F12_,F13=F13_,A2=A1,A1=L^2,alpha2=1,epsilon2=1,epsilon1=1,F23=F13_,dat,SI0,eqBE2);sol_:=fsolve({eqBE1_,eqBE2_},{T1,T2},T2=100..1000);T1_:=subs(sol_,T1*K_);'T1_'=TKC(%);T2_:=subs(sol_,T2*K_);'T2_'=TKC(%);eq12_BB_:=subs(T1=T1_,T2=T2_,A1=L^2,F12=F12_,epsilon1=epsilon,dat,eq12_BB); |
| (7) |
i.e. la placa soleada alcanzaría 94 ºC y transmitiría un calor de 1,5 W a la de atrás, que quedaría a 77 ºC (que es más de los 50 ºC permitidos).
f) Repetir el punto anterior pero con todas las caras pintadas de blanco.
A los intercambios netos de radiación entre dos superficies les seguiremos llamarndo Qij aunque no sean cuerpos negros (pese a que con ello podría haber Qij≠0 con Ti=Tj, en contra de la definición de calor).
Ya no puede ponerse Q21 en la forma anterior, dependiente solo de las dos temperaturas, y hay que recurrir al método de las exitancias, cuyo planteamiento es el siguiente:
| > | eq1:=(M1-M1bb)/((1-epsilon1)/(A1*epsilon1))=A1*F12*(M2-M1)+A1*F13*(M3-M1);eq2:=(M2-M2bb)/((1-epsilon2)/(A2*epsilon2))=A2*F21*(M1-M2)+A2*F23*(M3-M2);eq3:=(M1-M1bb)/((1-epsilon1)/(A1*epsilon1))=0;eq4:=(M2-M2bb)/((1-epsilon2)/(A2*epsilon2))=-alpha2*E*A2+epsilon2*A2*M2bb;M3:=0; |
| (8) |
Las ecuaciones 1 y 2 son las de balance neto de radiación recibida por 1 y por 2.
La eq3 es el balance de la cara 1 con la 1', y muestra que, como la cara 1 está aislada por detrás, entre lo que emite y lo que refleja sale como si emitiera un cuerpo negro.
La eq4 es el balance de la cara 2 con la 2', i.e. la radiación que llegua a la 2 (desde 1 y 3) ha de igualar a la que sale por 2' (hacia 3 menos el Sol).
Como siempre despreciamos la emitancia de fondo (M3) a 2,7 K
Entonces, para el caso de placas blancas (White & White):
| > | datWW:=alpha2=subs(dat,alpha),epsilon2=subs(dat,epsilon),epsilon1=subs(dat,epsilon);sol4:=solve({eq1,eq2,eq3,eq4},{M1,M1bb,M2,M2bb}):sol4_:=subs(datWW,F21=F12,F23=1-F12,F12=F12_,F13=F13_,dat,sol4);eqT:=T^4=Mbb/sigma;T1_:=evalf(subs(sol4_,dat,SI0,(M1bb/sigma)^(1/4)))*K_;'T1_'=TKC(%);T2_:=evalf(subs(sol4_,dat,SI0,(M2bb/sigma)^(1/4)))*K_;'T2_'=TKC(%);q12_WW:=Q21=A1*F12*(M2-M1);q12_WW_:=subs(sol4_,A1=L^2,F12=F12_,dat,%); |
| (9) |
i.e. la placa soleada alcanzaría -19 ºC y transmitiría un calor de 0,3 W a la de atrás, que quedaría a -34 ºC.
Podemos comprobar que si la placa soleada es negra y la de atrás blanca (i.e. Black & White), se recupera el resultado del apartado anterior (Black & Black).
| > | datBW:=alpha2=1,epsilon2=1,epsilon1=subs(dat,epsilon);sol4:=solve({eq1,eq2,eq3,eq4},{M1,M1bb,M2,M2bb}):sol4_:=subs(datBW,F21=F12,F23=1-F12,F12=F12_,F13=F13_,dat,sol4);eqT:=T^4=Mbb/sigma;T1_:=evalf(subs(sol4_,dat,SI0,(M1bb/sigma)^(1/4)))*K_;'T1_'=TKC(%);T2_:=evalf(subs(sol4_,dat,SI0,(M2bb/sigma)^(1/4)))*K_;'T2_'=TKC(%);q12_WW:=Q21=A1*F12*(M2-M1);q12_WW_:=subs(sol4_,A1=L^2,F12=F12_,dat,%); |
| (10) |
Exacto, la negra queda a 94 ºC, la blanca a 77 ºC, y se transmiten 1,5 W.
Otra manera de plantear el problema (eq1,eq2,eq3,eq4) sería mediante la analogía eléctrica, estableciendo un circuito eléctrico con nodos en las emitancias de cuerpo negro y las exitancias, resistencias superficiales y resistencias geométricas, y planteando en cada nudo el balance de intensidades de corriente:
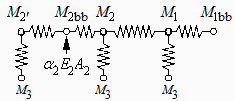
| > | M3:='M3':eq2p:=A2*F23*(M3-M2p)=(M2p-M2bb)/((1-epsilon2)/(A2*epsilon2));eq2bb:=(M2p-M2bb)/((1-epsilon2)/(A2*epsilon2))+alpha2*E*A2=(M2bb-M2)/((1-epsilon2)/(A2*epsilon2));eq2:=(M2bb-M2)/((1-epsilon2)/(A2*epsilon2))+A2*F23*(M3-M2)=A2*F21*(M2-M1);eq1:=A2*F21*(M2-M1)+A1*F13*(M3-M1)=(M1-M1bb)/((1-epsilon1)/(A1*epsilon1));eq1bb:=(M1-M1bb)/((1-epsilon1)/(A1*epsilon1))=0; |
| (11) |
y si eliminamos M2p entre las dos primeras, se vuelven a obtener la cuatro antedichas.
| > |