| > | restart:#"m11_p93". |
| > | read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):with(plots): |
1. Un radiador en un satélite geoestacionario está constituido por un panel en nido de abeja de 0,4 m de ancho, 0,5 m de largo, y 6 mm de espesor, formado por dos láminas de aluminio A6061 de 1 mm de espesor y un núcleo en panel de abeja del mismo material (de 4 mm de altura), de láminas de 10 m de espesor y 5 mm de anchura de celda. Dentro del panel está integrado el condensador de un tubo de calor (heat pipe) que evacúa 70 W y se va a aproximar por un conducto de 4×4 mm2 de sección, centrado en la anchura del panel (en contacto perfecto con las placas), que recorre sus 0,5 m de longitud, y que no debe sobrepasar los 65 ºC en órbita, ni debe bajar de 0 ºC en eclipse. La cara externa del radiador está recubierta de una fina capa de reflector solar (OSR), y las demás se supondrán aisladas. Se pide:
a) Establecer un modelo unidimensional no estacionario para la transmisión de calor por conducción a lo ancho del panel (desde el tubo hasta la periferia), calculando la conductividad efectiva.
b) Determinar el perfil de temperaturas que se tendría en un ensayo en tierra, teniendo en cuenta un coeficiente global de pérdidas de calor de 10 W/(m2·K) en la cara expuesta, y una temperatura del aire de 15 ºC que coincide con la inicial antes de comenzar la disipación de calor de 70 W (que se aproximará por un salto escalón).
c) Lo mismo, pero para un ensayo en vacío con 15 ºC de temperatura del recinto.
d) Calcular el transitorio en tierra.
e) Calcular el perfil estacionario en el ambiente espacial con sol frontal en perihelio, y sin sol en afelio.
f) Calcular el enfriamiento del panel si, a partir del estado estacionario con sol frontal en equinoccio, entra en eclipse.
g) Se quiere ahora estimar la bondad del modelo unidimensional considerando un modelo bidimensional para calcular la diferencia máxima de temperaturas entre las dos cars del panel, con sol frontal en régimen estacionario.
Datos:
| > | dat:=Lx=0.4*m_,Ly=0.5*m_,Lz=0.006*m_,Lzs=0.001*m_,Lzc=0.004*m_,delta=10e-6*m_,s=5e-3*m_,Q=70*W_,h=10*W_/(m_^2*K_),Tinf=(15+273.15)*K_,E0=1361*W_/m_^2,Ecc=0.0167,alpha=0.1,epsilon=0.8,k=180*W_/(m_*K_),rho=2710*kg_/m_^3,c=960*J_/(kg_*K_):dat:=dat,L=subs(dat,Lx/2);dat:=dat,Const,SI2,SI1: |
Se van a tomar para el A6061: k=180*W_/(m_*K_), rho=2710*kg_/m_^3, c=960*J_/(kg_*K_). Para el OSR se toma alpha=0.1 y epsilon=0.8.
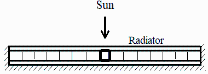
a) Establecer un modelo unidimensional no estacionario para la transmisión de calor por conducción a lo ancho del panel (desde el tubo hasta la periferia), calculando la conductividad efectiva.
El modelo 1D parece válido porque el espesor es pequeño y por el tubo de calor hay un plano de simetría, luego basta estuadiar T(x) desde x=0 (centro) hasta x=Lx/2=0,2 m (extremo), ya que el detalle de los 2 mm iniciales que ocupa el tubo es irrelevante con esta simplificación 1D. Considerando valores promedios en el espesor, el balance energético diferencial será:
| > | eqBEdif:=rho*A*Dx*c*Diff(T,t)=keff*A*Diff(T,x,x)*Dx+phi*A*Dx+p*Dx*(E-h*(T-Tinf)-epsilon*sigma*(T^4-Tinf^4));eqA:=A=Lz*Ly;eqA_:=subs(dat,%);eqp:=p=Ly;eqp_:=subs(dat,%); |
Para el núcleo en panal de abeja se tiene (nótese que conviene alinear las láminas del núcleo en la dirección x para mejorar la transmisión de calor):
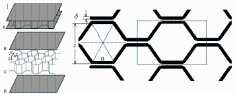
| > | keff_x:=k*(3/2)*delta/s;keff_x_:=subs(dat,%);keff_y:=k*delta/s;keff_y_:=subs(dat,%);keff_z:=k*(8/3)*delta/s;keff_z_:=subs(dat,%);rhoc_eff_x:=rho*c*(3*rho*c*delta)/(2*s);rhoc_eff_x_:=subs(dat,SI0,%)*J_/(m_^3*K_); |
i.e. a lo largo del eje x, el núcleo se comporta con k=0,54 W/(m·K), y con rho·c=20·10^9 J/(m3·K), que lo necesitaremos para los cálculos en transitorio. Para el panel en su conjunto, como la conducción de calor es en paralelo por las dos caras y el núcleo:
| > | eq_keff:=k=(ks*Lzs+kc*Lzc+kc*Lzs)/Lz;eq_keff:=k=(kA*Lzs+'keff_x'*Lzc+kA*Lzs)/Lz;eq_keff_:=k=subs(dat,(2*k*Lzs+keff_x_*Lzc)/Lz);eq_rhoc_eff:=rho*c=(2*rhoA*cA*Lzs+'rhoc_eff_x'*Lzc)/Lz;eq_rhoc_eff_:=rho*c=subs(dat,SI0,(2*rho*c*Lzs+rhoc_eff_x_*Lzc)/Lz)*J_/(m_^3*K_); |
i.e. el panel completo (dos láminas, 'skin', más núcleo, 'core') se comporta como un sólido de 6 mm de espesor y k=60 W/m·K) y rho·c=14·10^9 J/(m3·K); comprobamos que lo que más conduce son las caras de 1 mm, por lo que en primera aproximación sería k=kA*2/6=180·2/6=60 W/(m·K).
b) Determinar el perfil de temperaturas que se tendría en un ensayo en tierra, teniendo en cuenta un coeficiente global de pérdidas de calor de 10 W/(m2·K) en la cara expuesta, y una temperatura del aire de 15 ºC que coincide con la inicial antes de comenzar la disipación de calor de 70 W (que se aproximará por un salto escalón).
Este problema 1D estacionario admite solución analítica (Tabla 4, caso 3), siendo p=Ly el perímetro bañado, A=Ly·Lz el área de la sección de flujo de calor, y m=sqrt(h·p/(k·A)).
| > | eqBEdif:=rho*A*Dx*c*Diff(T,t)=k*A*Diff(T,x,x)*Dx-p*Dx*h*(T-Tinf);eqBEdif:=0=Diff(T,x,x)-m^2*(T-Tinf);aux:=(Q0/sqrt(p*h*k*A)):eq1:=(T(x)-Tinf)/aux=cosh(m*(L-x))/sinh(m*L);eq0:=T(0)=Tinf+aux/tanh(m*L);eqL:=T(L)=Tinf+aux/sinh(m*L);Q0:=Q/2;eqm:=m=sqrt(h*'p'/(k*A));h=subs(dat,h);'Q0'=subs(dat,Q0);eqm_:=m=evalf(subs(eq_keff_,eqA,eqp,dat,SI0,rhs(eqm)))/m_;eq0_:=T(0)=evalf(subs(eq_keff_,eqA,eqp,eqm_,dat,SI0,rhs(eq0)))*K_;T(0)=TKC(rhs(%));eqL_:=T(L)=evalf(subs(eq_keff_,eqA,eqp,eqm_,dat,SI0,rhs(eqL)))*K_;T(L)=TKC(rhs(%));L_:=subs(dat,SI0,L);eq1_:=evalf(subs(eq_keff_,eqA,eqp,eqm_,dat,SI0,eq1));eq1__:=T(x)=solve(subs(T(x)=T,eq1_),T);plot(rhs(eq1__)-273.15,x=0..L_,T_C=15..65); |
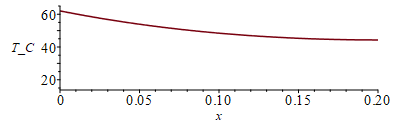 |
i.e. al disiparse Q/2=35 W desde el centro (x=0) hacia la derecha, a través del panel de k=61 W/(m·K), con pérdidas por la cara superior de h=10 W/(m2·K), se alcanza una Tmax=62 ºC en x=0 centro), y una Tmin=44 ºC en x=L=20 mm (borde aislado).
Podemos hacer una rápida comprobación estimando la Tmedia que evacuaría esos 35 W de un área de 0,2·0,5=0,1 m2 con un coeficiente h=10 W/(m2·K), resultando Tmedia=Tinf+Q0/(hLLy)=15+35/(10·0,2·0,5)=50 ºC. Vale.
c) Lo mismo, pero para un ensayo en vacío con 15 ºC de temperatura del recinto.
Ya no hay convección. Con radiación, el problema es no lineal y hay que resolverlo numéricamente.
| > | eqBEdif:=rho*A*Dx*c*Diff(T,t)=k*A*Diff(T,x,x)*Dx-p*Dx*epsilon*sigma*(T^4-Tinf^4);eqBEdif:=0=Diff(T,x,x)-(p/(k*A))*epsilon*sigma*(T^4-Tinf^4); |
| > | eq1:=diff(T(x),x,x)=subs(eq_keff_,eqA,eqp,dat,SI0,(p/(k*A))*epsilon*sigma*(T(x)^4-Tinf^4));eq0:=D(T)(0)=subs(eq_keff_,eqA,dat,SI0,-Q0/(k*A));eqL:=D(T)(L_)=0;sol_:=dsolve({eq1,eq0,eqL},numeric,'range'=0..0.2 ); |
| Error, (in dsolve/numeric/bvp) initial Newton iteration is not converging |
¡Vaya! no sabe resolver con condiciones de contorno de Newman (ni analítica ni numéricamente). Hacemos las iteraciones con condiciones iniciales a mano, y el resultado es:
| > | sol_:=[x=0,T(x)=0,Q(x)=0]:eq1:=diff(T(x),x,x)=subs(eq_keff_,eqA,eqp,dat,SI0,(p/(k*A))*epsilon*sigma*(T(x)^4-Tinf^4));eqL:=D(T)(L_)=0;for i from 300 to 400 by 10 while rhs(op(3,sol_(0)))>-184.6 do sol_:=dsolve({eq1,T(0)=i,eqL},numeric,'range'=0..0.2 );sol_(0);sol_(L_);od: sol_(0);sol_(L_);with(plots):pl:=odeplot(sol_,[x,T(x)-273.15],x=0..0.2):display(pl,'view'=[0..0.2,15..100]);Tmax:=rhs(op(2,sol_(0)))*K_;'Tmax'=TKC(%);Tmin:=rhs(op(2,sol_(L_)))*K_;'Tmin'=TKC(%); |
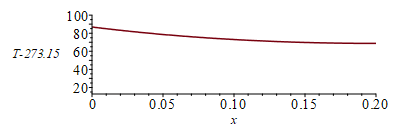 |
i.e. solo con radiación en el vacío a 15 ºC se calienta bastante más (Tmax=87 ºC, Tmin=69 ºC) que con convección (Tmax=62 ºC, Tmin=44 ºC), y se superaría el límite del enunciado (65 ºC).
Podemos hacer una rápida comprobación estimando la Tmedia que evacuaría esos 35 W de un área de 0,2·0,5=0,1 m2 con un eps=0,8, resultando:
| > | eqCheck:=Q0=epsilon*L*Ly*sigma*(Tm^4-Tinf^4);Tm_:=fsolve(subs(eqA,eqp,dat,SI0,%),Tm=200..500)*K_;'Tm_'=TKC(%); |
Puede valer, ya que Tm=75 ºC está entre Tmax=86 ºC y Tmin=69 ºC.
d) Calcular el transitorio en tierra.
Para el transitorio, tanto si es con aire o en vacío, hace falta el cálculo numérico.Sea N el número de tramos (N+1 puntos): 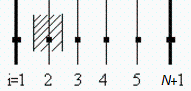
En general.
| > | eq_Heat_1D:=rho*c*diff(T(x,t),t)=k*diff(T(x,t),x,x)-(h*p/A)*(T(x,t)-Tinf)-(p/A)*epsilon*sigma*(T(x,t)^4-Tinf^4);i:='i':eqi_gen:=eq11_24_gen_;eqi:=subs(phi=0,%);eq0:=k*A*(T[1,j]-T[2,j])/Dx='Q0';eqN:=k*A*(T[N+1,j]-T[N,j])/Dx=0;eqN:=T[N+1,j+1]=T[N,j];eq0:=T[1,j+1]=T[2,j]+'Q0'*Dx/(k*A); |
![T[i, `+`(j, 1)] = `+`(T[i, j], `*`(Fo, `*`(`+`(T[`+`(i, 1), j], `-`(`*`(2, `*`(T[i, j]))), T[`+`(i, `-`(1)), j]))), `/`(`*`(phi, `*`(Dt)), `*`(rho, `*`(c))), `-`(`/`(`*`(p, `*`(Dt, `*`(`+`(`*`(h[lat],...](images/p93_60.gif) |
![T[i, `+`(j, 1)] = `+`(T[i, j], `*`(Fo, `*`(`+`(T[`+`(i, 1), j], `-`(`*`(2, `*`(T[i, j]))), T[`+`(i, `-`(1)), j]))), `-`(`/`(`*`(p, `*`(Dt, `*`(`+`(`*`(h[lat], `*`(`+`(T[i, j], `-`(T[infinity])))), `*`...](images/p93_61.gif) |
Podemos estimar la duración del transitorio suponiendo que solo hay conducción, lo cual nos dará un valor mínimo, ya que tardará más por estarse enfriando al aire.
| > | tc:=rho*c*L^2/k;eq_rhoc_eff_;tc_:=subs(%,eq_keff_,dat,tc);mass:=rho*L*Ly*(Lzs+(8/3)*(delta/s)*Lzc+Lzs);msss_=subs(dat,%);tc:='mass*c*DT/Q0';DT:=50*K_;tc_:=subs(mass=mass_,dat,tc); |
i.e. hay que contar con más de 1700 s (media hora) para que el salto disminuya a la mitad o así. A continuación veremos que hace falta mucho más tiempo, unos 10 000 s (casi 3 h) para que la diferencia sea insignificante. La otra estimación (tc=750 s) basada en despreciar las pérdidas al aire y calcular cuánto tarda en calentarse unos 50 ºC, se ve que es todavía peor.
En aire:
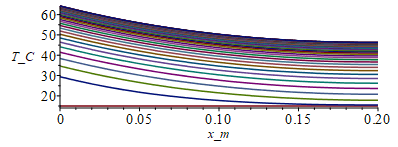
| > | N:=20;M:=5000;tsim:=10000;Dx:=subs(dat,L_/N);Dt:=evalf(tsim/M);Tinf_:=subs(dat,SI0,Tinf);Tn:=Matrix(1..M,1..N+1,Tinf_);eqFo:=Fo=k*'Dt'/(rho*c*'Dx'^2);Fo_:=subs(eq_keff_,eq_rhoc_eff_,dat,SI0,rhs(%));k_:=subs(SI0,rhs(eq_keff_));Dt_rcA:='Dt'/(rho*c*A);Dt_rcA_:=evalf(subs(eq_rhoc_eff_,eqA,dat,SI0,%));h_:=subs(dat,SI0,h);p_:=rhs(eqp_/m_);eps_:=0;sigma_:=subs(dat,SI0,sigma);T0_:=273.15:for j from 1 to M-1 do Tn[j+1,1]:=Tn[j,2]+subs(eq_keff_,eqA,dat,SI0,Q0*Dx/(k*A));Tn[j+1,N+1]:=Tn[j,N];for i from 2 to N do Tn[j+1,i]:=Tn[j,i]+Fo_*(Tn[j,i-1]-2*Tn[j,i]+Tn[j,i+1])-Dt_rcA_*p_*(h_*(Tn[j,i]-Tinf_)+eps_*sigma_*(Tn[j,i]^4-Tinf_^4));od:od:Tmax:=max(Tn)-T0_;Dm:=100:sx:=seq([seq([i*Dx-Dx,Tn[1+(j-1)*Dm,i]-T0_],i=1..N+1)],j=1..(M+1)/Dm):plot([sx],x_m=0..subs(dat,SI0,L),T_C=15..Tmax);st:=seq([seq([j*Dt-Dt,Tn[j,i]-T0_],j=1..M)],i=1..N+1):plot([st],t_s=0..tsim,T_C=15..Tmax); |
 |
 |
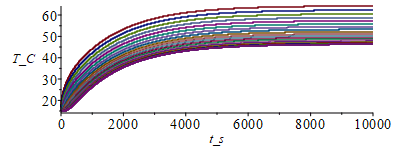 |
i.e. con esta discretización, Tmax=64 ºC en vez del teórico 62 ºC.
En vacío:
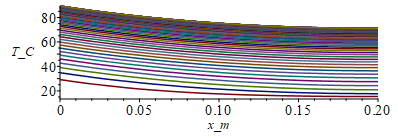
| > | N:=20;M:=8000;tsim:=15000;Dx:=subs(dat,L_/N);Dt:=evalf(tsim/M);Tinf_:=subs(dat,SI0,Tinf);Tn:=Matrix(1..M,1..N+1,Tinf_);eqFo:=Fo=k*'Dt'/(rho*c*'Dx'^2);Fo_:=subs(eq_rhoc_eff_,eq_keff_,dat,SI0,rhs(%));k_:=subs(SI0,rhs(eq_keff_));Dt_rcA:='Dt'/(rho*c*A);Dt_rcA_:=evalf(subs(eq_rhoc_eff_,eqA,dat,SI0,%));h_:=0;p_:=rhs(eqp_/m_);eps_:=subs(dat,epsilon);sigma_:=subs(dat,SI0,sigma);T0_:=273.15:for j from 1 to M-1 do Tn[j+1,1]:=Tn[j,2]+subs(eq_keff_,eqA,dat,SI0,Q0*Dx/(k*A));Tn[j+1,N+1]:=Tn[j,N];for i from 2 to N do Tn[j+1,i]:=Tn[j,i]+Fo_*(Tn[j,i-1]-2*Tn[j,i]+Tn[j,i+1])-Dt_rcA_*p_*(h_*(Tn[j,i]-Tinf_)+eps_*sigma_*(Tn[j,i]^4-Tinf_^4));od:od:Tmax:=max(Tn)-T0_;Dm:=100:sx:=seq([seq([i*Dx-Dx,Tn[j*Dm,i]-T0_],i=1..N+1)],j=1..M/Dm):plot([sx],x_m=0..subs(dat,SI0,L),T_C=15..Tmax);st:=seq([seq([j*Dt-Dt,Tn[j,i]-T0_],j=1..M)],i=1..N+1):plot([st],t_s=0..tsim,T_C=15..Tmax); |
 |
 |
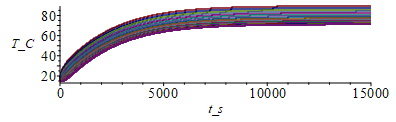 |
i.e. con esta discretización, Tmax=89 ºC en vez del teórico 87 ºC.
e) Calcular el perfil estacionario en el ambiente espacial con sol frontal en perihelio, y sin sol en afelio.
Podríamos seguir con la simulación transitoria desde cualquier estado inicial, pero resolveremos directamente el estacionario. Como antes, conviene hacer una estimación previa, suponiendo una T uniforme, Tu, resolviendo el BE: EA+Q=eAsT4.
Con sol frontal en perihelio:
| > | eqBE:=alpha*E_peri*L*Ly+'Q0'=epsilon*L*Ly*sigma*Tu^4;eqE:=E_peri=E0*(1+Ecc)^2;E_peri_:=subs(dat,SI0,rhs(%));eqBE_:=subs(E_peri=E_peri_,dat,SI0,eqBE);Tu_:=fsolve(%,Tu=200..500)*K_;'Tu_'=TKC(%);sol_:=[x=0,T(x)=0,Q(x)=0]:eq1:=diff(T(x),x,x)=(p/(k*A))*(-alpha*E_peri+epsilon*sigma*(T(x)^4-0));eq1:=diff(T(x),x,x)=subs(eq_keff_,eqA,eqp,dat,SI0,(p/(k*A))*(-alpha*E_peri_+epsilon*sigma*(T(x)^4-0)));eqL:=D(T)(L_)=0;for i from 300 to 400 by 1 while rhs(op(3,sol_(0)))>-184.6 do sol_:=dsolve({eq1,T(0)=i,eqL},numeric,'range'=0..0.2 );sol_(0);sol_(L_);od: sol_(0);sol_(L_);with(plots):pl:=odeplot(sol_,[x,T(x)-273.15],x=0..0.2):display(pl,'view'=[0..0.2,0..60]);Tmax:=rhs(op(2,sol_(0)))*K_;'Tmax'=TKC(%);Tmin:=rhs(op(2,sol_(L_)))*K_;'Tmin'=TKC(%); |
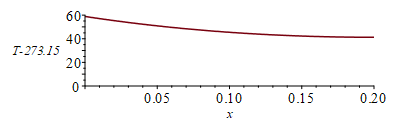 |
i.e. la estimación uniforme con sol frontal da Tu=49 ºC, y en realidad llega a Tmax=59 ºC y Tmin=41 ºC.
Sin sol en afelio (nótese que si no le da el sol, no importa si es afelio o perihelio):
| > | eqBE:='Q0'=epsilon*L*Ly*sigma*Tu^4;eqBE_:=subs(dat,SI0,eqBE);Tu_:=fsolve(%,Tu=200..500)*K_;'Tu_'=TKC(%);sol_:=[x=0,T(x)=0,Q(x)=0]:eq1:=diff(T(x),x,x)=(p/(k*A))*(epsilon*sigma*(T(x)^4-0));eq1:=diff(T(x),x,x)=subs(eq_keff_,eqA,eqp,dat,SI0,(p/(k*A))*(epsilon*sigma*(T(x)^4-0)));eqL:=D(T)(L_)=0;for i from 300 to 400 by 1 while rhs(op(3,sol_(0)))>-184.6 do sol_:=dsolve({eq1,T(0)=i,eqL},numeric,'range'=0..0.2 );sol_(0);sol_(L_);od: sol_(0);sol_(L_);with(plots):pl:=odeplot(sol_,[x,T(x)-273.15],x=0..0.2):display(pl,'view'=[0..0.2,0..60]);Tmax:=rhs(op(2,sol_(0)))*K_;'Tmax'=TKC(%);Tmin:=rhs(op(2,sol_(L_)))*K_;'Tmin'=TKC(%); |
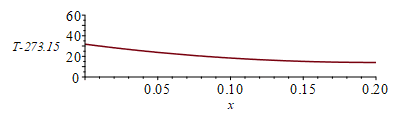 |
i.e. la estimación uniforme sin sol da Tu=23 ºC, y en realidad llega a Tmax=33 ºC y Tmin=15 ºC.
f) Calcular el enfriamiento del panel si, a partir del estado estacionario con sol frontal en equinoccio, entra en eclipse.
Lo primero habría que calcular el estacionario con sol equinoccial (y no en perihelio):
| > | sol_:=[x=0,T(x)=0,Q(x)=0]:eq1:=diff(T(x),x,x)=(p/(k*A))*(-alpha*E0+epsilon*sigma*(T(x)^4-0));eq1:=diff(T(x),x,x)=subs(eq_keff_,eqA,eqp,dat,SI0,(p/(k*A))*(-alpha*E0+epsilon*sigma*(T(x)^4-0)));eqL:=D(T)(L_)=0;for i from 300 to 400 by 1 while rhs(op(3,sol_(0)))>-184.6 do sol_:=dsolve({eq1,T(0)=i,eqL},numeric,'range'=0..0.2 );sol_(0);sol_(L_);od: sol_(0);sol_(L_);with(plots):pl:=odeplot(sol_,[x,T(x)-273.15],x=0..0.2):display(pl,'view'=[0..0.2,0..60]);Tmax:=rhs(op(2,sol_(0)))*K_;'Tmax'=TKC(%);Tmin:=rhs(op(2,sol_(L_)))*K_;'Tmin'=TKC(%); |
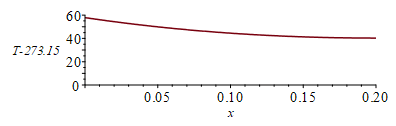 |
Bueno, apenas hay diferencia: entra estos valores en el equinoccio (Tmax=58 ºC y Tmin=40 ºC) y los de perihelio (Tmax=59 ºC y Tmin=41 ºC).
El eclipse equinoccial en GEO dura 71 minutos (hay 2 min de penumbra a la entrada, 69 min de eclipse total, y otros 2 min de penumbra a la salida). El periodo orbital es casi 24 h (86164 s).
Nota. Si el radiador mantiene una orientación fija respecto a la Tierra, lo cual es lo normal en satélites geoestacionarios con radiador integrado, y si al entrar en eclipse le da el sol frontal, se deduce que este radiador apunta siempre al centro de la Tierra, por lo que habrá pasado un cuarto de órbita antes (6 h antes) por una posición sin sol (sol a haces con el radiador), y a partir de ahí la inclinación solar irá aumentando, y la irradiancia solar con el coseno del ángulo zenital, por lo que el perfil de temperatura siempre irá un poco retrasado (se necesita un tiempo de unas 4 h (15 000 s) para alcanzar el régimen con salto escalón, y han pasado 6 h con salto cosenoidal.
Al entrar en eclipse deja de darle el sol (casi es un salto escalón porque la penumbra dura 2 minutos) y el radiador empieza a enfriarse hasta que acaba el eclipse y velve la insolación frontal.
Simulamos solo desde que entra al eclipse hasta que sale 71 min después.
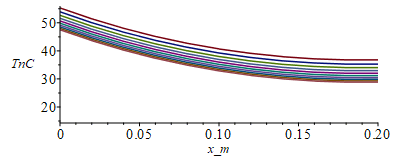
| > | tGEO_eclipse_max:=71*60*s_;N:=10;M:=1000;tsim:=tGEO_eclipse_max/s_;Dx:=subs(dat,L_/N);Dt:=evalf(tsim/M);Tinf_:=2.7;Tn:=Matrix(1..M,1..N+1,300);for i from 1 to N do Tn[1,i]:=rhs(op(2,sol_(i*L_/N))); od:eqFo:=Fo=k*'Dt'/(rho*c*'Dx'^2);Fo_:=subs(eq_rhoc_eff_,eq_keff_,dat,SI0,rhs(%));k_:=subs(SI0,rhs(eq_keff_));Dt_rcA:='Dt'/(rho*c*A);Dt_rcA_:=evalf(subs(eq_rhoc_eff_,eqA,dat,SI0,%));h_:=0;p_:=rhs(eqp_/m_);eps_:=subs(dat,epsilon);sigma_:=subs(dat,SI0,sigma);E_eclipse_:=0;T0_:=273.15:for j from 1 to M-1 do Tn[j+1,1]:=Tn[j,2]+subs(eq_keff_,eqA,dat,SI0,Q0*Dx/(k*A));Tn[j+1,N+1]:=Tn[j,N];for i from 2 to N do Tn[j+1,i]:=Tn[j,i]+Fo_*(Tn[j,i-1]-2*Tn[j,i]+Tn[j,i+1])-Dt_rcA_*p_*(h_*(Tn[j,i]-Tinf_)+eps_*sigma_*(Tn[j,i]^4-Tinf_^4));od:od:Tmax:=max(Tn)-T0_;Tmin:=min(Tn)-T0_;Dm:=100:sx:=seq([seq([i*Dx-Dx,Tn[j*Dm,i]-T0_],i=1..N+1)],j=1..M/Dm):plot([sx],x_m=0..subs(dat,SI0,L),TnC=15..Tmax);st:=seq([seq([j*Dt-Dt,Tn[j,i]-T0_],j=1..M)],i=1..N+1):plot([st],t_s=0..tsim,T_C=15..Tmax); |
 |
 |
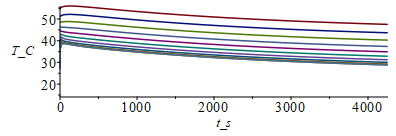 |
i.e. el radiador se enfría unos 15 ºC (e.g. entra al eclipse con Tmin=41 ºC y sale con Tmin=27 ºC (el pequeño calentamiento inicial que puede apreciarse en este último gráfico no es real; es debido a que las condiciones de entrada se han calculado por un procedimiento distinto al transitorio).
g) Se quiere ahora estimar la bondad del modelo unidimensional considerando un modelo bidimensional para calcular la diferencia máxima de temperaturas entre las dos cars del panel, con sol frontal en régimen estacionario.
Como la conductividad a lo largo de las caras (de 1 mm de espesor de aluminio, k=180 W/(m·K)) es mucho mayor que las del núcleo de celdillas (kx=0,54 W/(m·K) y kz=0,96 W/(m·K)), el modelo bidimensional más sencillo es:
-Para la cara superior (la radiante, 1), su T1(x,y) solo depende de x, y esta T1(x) recibe un calor 35/2=17,5 W en x=0, va perdiendo calor hacia arriba por radiación y ganando algo por abajo por conducción a través del núcleo, hasta su extremo aislado.
-Para el núcleo, despreciando el flujo de calor que le llega en la dirección x frente al que fluye en dirección y, su Tc(x,y) será una superfice reglada formada por líneas rectas que unen en cada punto x la T2(x) con la T1(x).
-Para la cara inferior, su T2(x,y) solo depende de x, y esta T2(x) recibe un calor 35/2=17,5 W en x=0, y lo va perdiendo hacia arriba por conducción a través del núcleo, hasta su extremo aislado.
Se trata pues de dos ecuaciones diferenciales acopladas:
| > | deq1:=k*Ly*Lzs*diff(T1(x),x,x)=Ly*epsilon*sigma*(T1(x)^4-0)-Ly*kc*(T2(x)-T1(x))/Lzc;deq2:=k*Ly*Lzs*diff(T2(x),x,x)=Ly*kc*(T2(x)-T1(x))/Lzc;kc:=keff_z;'kc'=subs(dat,%);eq10:=k*Ly*Lzs*diff(T1(x),x)[x=0]=-'Q0'/2;eq1L:=k*Ly*Lzs*diff(T1(x),x)[x=L]=0;eq20:=k*Ly*Lzs*diff(T2(x),x)[x=0]=-'Q0'/2;eq2L:=k*Ly*Lzs*diff(T2(x),x)[x=L]=0;eq10_:=Tprime(0)=-Q0/(2*k*Ly*Lzs);Tprime_:=subs(dat,SI0,rhs(%)); |
| > | deqs:=subs(dat,SI0,[deq1,deq2,T1(0)=ii,T2(0)=ii,D(T1)(L_)=0,D(T2)(L_)=0]);sol_:=[x=0,T1(x)=0,Q(x)=0,T2(x)=0,Q(x)=0]:for i from 300 to 400 by 1 while rhs(op(3,sol_(0)))>Tprime_ do sol_:=dsolve(subs(ii=i,deqs),numeric,'range'=0..L_ );sol_(0);sol_(L_);od: sol_(0);sol_(L_);pl1:=odeplot(sol_,[x,T1(x)-273.15],x=0..L_):pl2:=odeplot(sol_,[x,T2(x)-273.15],x=0..L_):display({pl1,pl2});T1end:=rhs(op(2,sol_(L_)))*K_;'T1end'=TKC(%);T2end:=rhs(op(4,sol_(L_)))*K_;'T2end'=TKC(%); #,'view'=[0..0.2,0..100] |
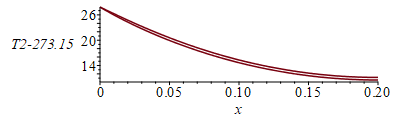 |
i.e. apenas hay 11,2-10,6=0,6 ºC de diferencia entre los extremos de las caras (en x=L), lo que justifica el modelo 1D. Pero si el núcleo no hubiera sido de hoja de aluminio sino de otro material más aislante, probaremos a dividir por 10 la k_core (o la delta, porque la kcore ya está fija):
| > | deqs:=subs(delta=delta/10,dat,SI0,[deq1,deq2,T1(0)=ii,T2(0)=ii,D(T1)(L_)=0,D(T2)(L_)=0]);sol_:=[x=0,T1(x)=0,Q(x)=0,T2(x)=0,Q(x)=0]:for i from 300 to 400 by 1 while rhs(op(3,sol_(0)))>Tprime_ do sol_:=dsolve(subs(ii=i,deqs),numeric,'range'=0..L_ );sol_(0);sol_(L_);od: sol_(0);sol_(L_);pl1:=odeplot(sol_,[x,T1(x)-273.15],x=0..L_):pl2:=odeplot(sol_,[x,T2(x)-273.15],x=0..L_):display({pl1,pl2});T1end:=rhs(op(2,sol_(L_)))*K_;'T1end'=TKC(%);T2end:=rhs(op(4,sol_(L_)))*K_;'T2end'=TKC(%); #,'view'=[0..0.2,0..100] |
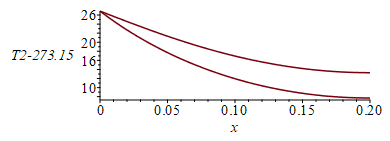 |
i.e. si la resistencia térmica del núcleo fuese 10 veces mayor, el salto en el extremo pasaría de ser 0,6 ºC a ser 13,3-7,7=5,6 ºC, i.e. aumentaría proporcioalmente.
También se podría añadir a este estudio el efecto de la caída de temperatura a lo largo del tubo de calor, aunque es de esperar que sea pequeña (unos pocos grados).
Como nota final, este ejercicio podría servir para optimizar el diseño de un radiador con conductos de calor embebidos, estudiando el efecto de los materiales y la geometría, considerando varios tubos de calor distribuidos en la anchura del panel (en lugar de solo uno como se hace aquí).
En conclusión, se está dentro de los requisitos térmicos: ni se superan los 65 ºC ni se baja a 0 ºC.
| > |