p511.html

> restart:#"m07_p51"

Un depósito rígido de 10 m3 contiene inicialmente aire a 100 kPa y 300 K. A partir de un cierto instante se pone en comunicación con un gran depósito de O2 a 300 kPa y 300 K a través de una pequeña tubería. Se pide:
a) Plantear los balances másicos y energético desde el inicio hasta un instante intermedio en que ha entrado una masa m.
b) Determinar el estado final suponiendo que el proceso es muy lento.
c) Determinar el estado final (hasta el equilibrio mecánico) suponiendo que el proceso es muy rápido.
d) Temperatura que se alcanzaría en el interior en el caso anterior.
e) Intercambio de calor con el ambiente en el caso de proceso lento.
Datos:

> read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):Digits:=5:

> su1:="O2":su2:="N2":dat:=[V=10*m_^3,xN=0.79,xO=0.21,T1=300*K_,p1=100e3*Pa_,p2=300e3*Pa_];

> datO:=get_gas_data(su1):cpO=subs(%,Const,c[p]*M);datN:=get_gas_data(su2):cpN=subs(%,Const,c[p]*M);dat:=c[p]=29*J_/(mol_*K_),op(dat),Const,SI2,SI1:

(1)

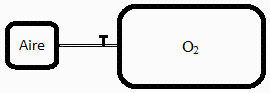
a) Plantear los balances másicos y energético desde el inicio hasta un instante intermedio en que ha entrado una masa m.

Todo se centra en el análisis del depósito pequeño: un proceso de llenado (ver 'Llenado y vaciado de depósitos a presión'). Las condiciones en el depósito grande no cambian (por su tamaño).

Como es una mezcla variable de gases, usamos valores molares. Tomamos como sistema el contenido del depósito (volumen de control rígido, W=0).

Para las energías tomamos el origen en T=0 K. Como ambos gases son diatómicos, consideramos iguales sus cp molares.

> eqBMN:=nN=nNini;eqBMO:=nO=nOini+Dn;eqBE:=E2-E1=Q+W+h[entra]*(n[fin]-n[ini]);W:=0;eqBE:=(nO+nN)*c[v]*T2-(nOini+nNini)*c[v]*T1=Q+W+c[p]*T1*(nO-nOini);eqBE_:=subs(c[v]=c[p]-R[u],eqBMN,eqBMO,eqBE);eqBE__:=%:

(2)

Aparte de estas ecuaciones, tenemos las ecuaciones de estado inicial y final:

> eqE1:=p1*V=n1*R[u]*T1;n1_:=subs(dat,solve(%,n1));nOini_:=subs(dat,c21*n1_);nNini_:=subs(dat,c79*n1_);eqE2:=p*V=(n1+Dn)*R[u]*T2;

(3)

Dado Dn (Dn=Dm/MO), necesitamos saber cuánto y cómo se llena para determinar el estado 2.

b) Determinar el estado final suponiendo que el proceso es muy lento.

Si es muy lento será isotermo (T2=T1), y como se llenará hasta que haya equilibrio (hasta alcanzar la presión del depósito grande):

> eqp2:=p2=subs(dat,p2);eqT2:=T2=subs(dat,T1);eqE2_:=subs(p=p2,eqE2);Dn_:=subs(T2=T1,n1=n1_,dat,solve(%,Dn));eqBMN:=nN2=nNini_;eqBMO:=nO2=nOini_+Dn_;Dn__:=Dn_:m_ini:=nOini*MO+nNini*MN;m_ini_:=nOini_*subs(datO,M)+nNini_*subs(datN,M);m_fin_:=subs(eqBMO,datO,nO2*M)+subs(eqBMN,datN,nN2*M);

(4)

i.e. si se alcanza el equilibrio de presiones lentamente, entran 802 mol de O2 y queda todo (los 401+802=1203 mol totales) a 300 K.

El balance energético determinaría el calor evacuado.

c) Determinar el estado final (hasta el equilibrio mecánico) suponiendo que el proceso es muy rápido.

Si es muy rápido será Q=0 y los gases se calentarán al entrar (por el trabajo de compresión de lo que va entrando). Ahora tenemos 2 incógnitas: Dn y T2.

> eqE:=eqE2_;eqBE:=subs(Q=0,eqBE_);eqE_:=subs(eqp2,n1=n1_,nNini=nNini_,nOini=nOini_,dat,SI0,eqE);eqBE_:=subs(n1=n1_,nNini=nNini_,nOini=nOini_,dat,SI0,eqBE);sol_:=solve({eqE_,eqBE_},{Dn,T2})[1];T2_:=subs(sol_,T2*K_);Dn_:=subs(sol_,Dn*mol_);

(5)

i.e. si la entrada es rápida sólo entran 572 mol (en vez de 802 mol), y el gas se calienta hasta 371 K (desde los 300 K iniciales).

d) Temperatura que se alcanzaría en el caso anterior.

Visto, 371 K (98 ºC).

e) Intercambio de calor con el ambiente en el caso de proceso lento.

> eqBE__;T2=T1;eqBE___:=Dn*R[u]*T1=Q;'Dn_'=Dn__;Q_:=subs(dat,Dn__*R[u]*T1);

(6)

i.e. salen 2 MJ del sistema en forma de calor. Como los gases no cambian de temperatura (no acumulan energía), este calor que sale es igaul al trabajo de flujo que entra, V·Dp=10·(300-100)=2000 kJ.