p66.mw
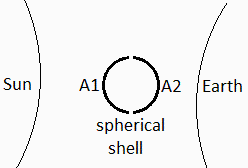
Consider a spherical shell 0.1 m in diameter and 1 mm thick, made of titanium. Find:
a) At what distance to the Sun would it reach its melting temperature, assumed isothermal.
b) What temperature would attain such a sphere, painted black, in the immediate proximity to the Sun.
c) To enhance the thermal model, consider two nodes for the sphere, and find the conductive and the radiative couplings, and the new temperatures at the previous locations.
d) Now consider the sphere in LEO at 300 km altitude, and find the temperature corresponding to its steady state at the subsolar point and at the opposite one.
Data for titanium from solid_data and thermooptic_data.
read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):with(plots):with(RealDomain):assume(t>0,tau>0):unprotect(D):
| > |
su:="Titanio":dat:=[D=0.1*m_,delta=1e-3*m_,E=1360*W_/m_^2,R[SE]=150e9*m_,H=300e3*m_,epsilon[p]=0.615,rho[p]=0.3,Tp=288.15*K_,Tinf=2.7*K_,TS=5800*K_,R[S]=0.7e9*m_];dat:=op(dat),get_sol_data(su),Const,SI2,SI1:alpha=subs(dat,alpha);epsilon=subs(dat,epsilon); |
a) At what distance to the Sun would it reach its melting temperature, assumed isothermal.
Thr melting temperature of titanium is so high (>>1000 K) that the two-band spectral model is no longer valid. However, having alpha=epsilon, alleviates the problem.
Let R[Ss] be the distance to the Sun's centre.
| > |
Tm_:=subs(dat,T[f]);eqEB:=m*c*dT/dt=Qin-Qout;eqBE:=0=Qs-Qinf;Qs:=alpha*E*(R[SE]/R[Ss])^2*Pi*D^2/4;Qinf:=epsilon*Pi*D^2*sigma*(T^4-Tinf^4);eqTst:=T[f]=sqrt(sqrt(Qs/(epsilon*Pi*D^2*sigma)));eq:=R[Ss]=fsolve(subs(dat,SI0,%),R[Ss])*m_;R[Ss]=subs(dat,rhs(%)*ua_/R[SE]);R[Ss]/R[S]=rhs(eq)/subs(dat,R[S]);Qs_:=subs(eq,dat,Qs); |
i.e. the titanium sphere would melt if closer than 2.7e9 m to the Sun (i.e. at 0.02 astronomical units), what is still 2.9 Sun radii away of its surface (3.9 radii from Sun's centre). At such small distances to the Sun, the asumptio of parallel rays may not be accurate. If we compute Qs from viewfactors:
| > |
Qs:=alpha*As*FsS*sigma*TS^4;As:=Pi*D^2;As_:=subs(dat,%);FsS:=(1-sqrt(1-1/h^2))/2;h_:=rhs(eq)/subs(dat,R[S]);FsS_:=subs(h=h_,dat,FsS);Qs_:=subs(h=h_,dat,Qs); |
i.e. being so near the Sun, the sphere gets 20.5 kW from it instead of 19.6 kW (higher because it gets some solar radiation on the rear. Hence, the correct distance is:
| > |
Qs:='Qs':eqTst:=T[f]=sqrt(sqrt(Qs/(epsilon*As*sigma)));Qs:=alpha*As*FsS*sigma*TS^4:FsS_:=subs(dat,epsilon*As*sigma*T[f]^4/(alpha*As*sigma*TS^4));h_:=solve(FsS=FsS_,h)[1]; |
i.e. the titanium sphere would melt at a relative distance of h=3.96 Sun's radii (instead of at 3.87). Only FsS=1.6 % of the radiation coming out of the sphere reaches the Sun
b) What temperature would attain such an sphere, painted black, in the immediate proximity to the Sun.
| > |
eqEB:=0='Qs-Qinf';h=1;FsS_:=subs(h=1,FsS);eqEB_:=subs(h=1,alpha=1,epsilon=1,eqEB);eqEB__:=subs(h=1,dat,SI0,eqEB_);T_:=fsolve(%,T=10..10000)*K_;'Ts_'=TKC(%);Qs_:=subs(h=1,dat,Qs); |
i.e. it would attain 4880 K, in spite of being 'touching' the Sun at 5800 K (the explanation is that only gets solar radiation from one side while emitting from all around), 605 kW in total. We can mention that a flat plate would reach the same temperature (F12=1/2 too), and that titanium, with alpha=epsilon, would get the same temperature as a blackbody (if it could stand it), but absorbing only 605*0.6=363 kW.
c) To enhance the thermal model, consider two nodes for the sphere, and find the conductive and the radiative couplings, and the new temperatures at the previous locations.
Let T1 be the temperature of the hemispherical shell lit (frontal) and T2 that of the other. The energy balance is:
| > |
eqEB1:=0=Qrad1-Qcond12-Qrad_int12;eqEB2:=0=Qrad2+Qcond12+Qrad_int12; |
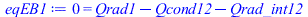 |
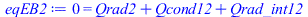 |
(5) |
We must account for the conductive coupling, and for the internal and external radiative couplings.
Conductive coupling, i.e. heat conduction through the contact area Pi*D*delta. We assume a characteristic heat-path length of one radius between hemispheres.
| > |
Qcond12:=k*Pi*D*delta*(T1-T2)/L;L=D/2;Qcond12:=k*Pi*D*delta*(T1-T2)/(D/2);Qcond12_:=subs(dat,SI0,%); |
Radiative coupling through the interiror. Blackbodies. View factor between two hemispheres in contact (forming a sphere), F12=1/2.
| > |
Qrad_int12:=A1*F12*sigma*(T1^4-T2^4);eqA1:=A1=Pi*D^2/2;eqA1_:=subs(dat,%);F12=1/2;Qrad_int12_:=subs(eqA1_,F12=1/2,dat,SI0,Qrad_int12); |
Radiative coupling through the exteriror.
| > |
Qrad1:=Qrad1S-Qrad1inf;Qrad1S:=alpha*A1*F1S*sigma*TS^4;Qrad1inf:=epsilon*A1*sigma*T1^4;Qrad2:=Qrad2S-Qrad2inf;Qrad2S:=alpha*A1*F2S*sigma*TS^4;Qrad2inf:=epsilon*A1*sigma*T2^4; |
From VF-Tables (Small hemisphere to large frontal sphere), the view factor for hemisphere 1 is:
| > |
eqF1S:=F[1,S]=(1-sqrt(1-1/h^2)+1/(2*h^2))/2;eqh:=h=R[Ss]/R[S];eq;eqh_:=subs(eq,dat,eqh);eqF1S_:=subs(eqh_,eqF1S);h=1;eqF1S_1:=subs(h=1,eqF1S) |
i.e. if the sphere was touching the Sun (h=1), only 3/4 of its emission would impingo on the Sun, and it is were at h=3.9 just a mere 3 % of its emission would reach the Sun.
For the opposite hemisphere 2, from the view-factor composition relation F[1+2,3]=(A1*F12+A2*F23)/(A1+A2) and the whole sphere view factor (same Table):
| > |
eqF2S:=F[2,S]=2*F[1+2,S]-F[1,S];eqF12S:=F[1+2,S]=(1-sqrt(h^2-1)/h)/2;eqF2S_:=subs(%,eqF1S,eqh_,eqF2S);eqF2S_1:=subs(eqF1S_1,eqF12S,h=1,eqF2S); |
we find that F[2,S]=1/4 for the touching position (h=1), and F[2,S]=0.0003 for h=3.9.
Hence, for the h=1 case:
| > |
Qrad1_:=subs(eqA1_,F1S=rhs(eqF1S_1),TS=5800*K_,dat,SI0,Qrad1);Qrad2_:=subs(eqA1_,F2S=rhs(eqF2S_1),TS=5800*K_,dat,SI0,Qrad2);eqEB1_:=0=Qrad1_-Qcond12_-Qrad_int12_;eqEB2_:=0=Qrad2_+Qcond12_+Qrad_int12_;sol_:=fsolve({eqEB1_,eqEB2_},{T1,T2},{T1=1000..6000,T2=100..5000}); |
i.e. the lit hemisphere arrives at T1=5090 K (it was 4880 K before), whereas the opposite one attains 4630 K (4880 K before).
For h=3.9:
| > |
Qrad1_:=subs(eqA1_,F1S=rhs(eqF1S_),TS=5800*K_,dat,SI0,Qrad1);Qrad2_:=subs(eqA1_,F2S=rhs(eqF2S_),TS=5800*K_,dat,SI0,Qrad2);eqEB1_:=0=Qrad1_-Qcond12_-Qrad_int12_;eqEB2_:=0=Qrad2_+Qcond12_+Qrad_int12_;sol_:=fsolve({eqEB1_,eqEB2_},{T1,T2},{T1=10..5000,T2=10..5000}); |
i.e. when the shell is at 0.02 ua (2.9 Sun-radii to Sun's surface), the lit hemisphere attains 2260 K, and the opposite one 1870 K; in the 1-node model they both reached 2070 K).
d) Now consider the sphere in LEO at 300 km altitude, and find the temperature corresponding to its steady state at the subsolar point and at the opposite one.
Firs with the 1 node model.
| > |
Fsp:=FsS;eqh:=h=R[LEO]/R[T];subs(R[LEO]=R[T]+H,%);eqh_:=subs(dat,%);Fsp_:=subs(eqh_,FsS);Qs:='Qs':eqEB_0:=m*c*dT/dt='Qs+Qp+Qa-Qinf';Qs:=alpha*Pi*D^2*E/4;Qs_:=subs(dat,Qs);Qp:=epsilon*As*'Fsp'*sigma*epsilon[p]*Tp^4;Qp_:=subs(eqh_,dat,%);Qa_0:=alpha*As*'Fsp'*rho[p]*E;Qa_0_:=subs(eqh_,dat,%);Qinf:=epsilon*As*sigma*T^4;Tst_LEO_0:=subs(dat,SI0,sqrt(sqrt((Qs_+Qp_+Qa_0_)/(epsilon*As*sigma))))*K_;'Tst_LEO_0'=TKC(%);eqEB_180:=m*c*dT/dt='Qp-Qinf';Tst_LEO_180:=subs(dat,SI0,sqrt(sqrt((Qp_)/(epsilon*As*sigma))))*K_;'Tst_LEO_180'=TKC(%); |
i.e. for a sphere in LEO (at h=1.05 Earth's radii), the planet view factor is Fsp=0.35, and it would attain 317 K (43 ºC) at the subsolar point (absorbing 6.4 W solar plus 2.7 W albedo plus 1.6 W IR), and 197 K (-77 ºC) at the opposite point.
Now for the two-nodes model (1=facing Earth):
| > |
F1p:=rhs(eqF1S);F1p_:=subs(eqh_,%);F2p:='2*Fsp-F1p';F2p_:=subs(eqh_,%); |
At subsolar point:
| > |
eqEB_0_1:=0=Qcond21+Qrad_int21+Qp1+Qa1-Qinf1;Qcond21:=-'Qcond12';Qrad_int21:=-'Qrad_int12';Qp1:=epsilon*A1*'F1p'*sigma*epsilon[p]*Tp^4;Qp1_:=subs(eqh_,eqA1_,dat,%);Qa1:=alpha*A1*'F1p'*rho[p]*E;Qa1_:=subs(eqh_,eqA1_,dat,%);Qinf1:=epsilon*A1*sigma*T1^4;eqEB_0_1_:=subs(F12=F1p,eqh_,eqA1_,dat,SI0,eqEB_0_1);eqEB_0_2:=0=Qs2+Qp2+Qa2-'Qcond21'-'Qrad_int21'-Qinf2;Qs2:=alpha*A[frontal]*E;Qs2_:=subs(A[frontal]=A1/2,eqA1_,dat,%);Qp2:=subs(F1p='F2p',Qp1);Qp2_:=subs(eqh_,eqA1_,dat,%);Qa2:=alpha*A1*'F2p'*rho[p]*E;Qa2_:=subs(eqh_,eqA1_,dat,%);Qinf2:=epsilon*A1*sigma*T2^4;eqEB_0_2_:=subs(A[frontal]=A1/2,F12=F2p,eqh_,eqA1_,dat,SI0,eqEB_0_2);sol_:=fsolve({eqEB_0_1_,eqEB_0_2_},{T1,T2},{T1=1..1000,T2=1..400});T1_0:=subs(sol_,T1)*K_;'T1_0'=TKC(%);T2_0:=subs(sol_,T2)*K_;'T2_0'=TKC(%); |
i.e. the hemisphere facing the Earth attains T1=42 ºC and the other (facing the Sun) T2=51 ºC; it was 43 ºC before. Notice that the sum of heat absorptions coincides.
At point opposite subsolar one:
| > |
eqEB_180_1:=0='Qcond21+Qrad_int21+Qp1-Qinf1';'Qp1'=Qp1_;eqEB_180_1_:=subs(F12=F1p,eqh_,eqA1_,dat,SI0,eqEB_180_1);eqEB_180_2:=0='-Qcond21-Qrad_int21+Qp2-Qinf2';'Qp2'=Qp2_;eqEB_180_2_:=subs(F12=F2p,eqh_,eqA1_,dat,SI0,eqEB_180_2);sol_:=fsolve({eqEB_180_1_,eqEB_180_2_},{T1,T2},{T1=1..1000,T2=1..400});T1_0:=subs(sol_,T1)*K_;'T1_0'=TKC(%);T2_0:=subs(sol_,T2)*K_;'T2_0'=TKC(%); |
i.e. ; the cap facing the Earth attains 197 K (-76 ºC), and the other cap 194 K (-80 ºC); when together, it was 197 K (-77 ºC).

![`+`(`/`(`*`(`/`(1, 4), `*`(alpha, `*`(E, `*`(`^`(R[SE], 2), `*`(Pi, `*`(`^`(D, 2))))))), `*`(`^`(R[Ss], 2))))](images/p661_9.gif)
![T[f] = `+`(`*`(`/`(1, 2), `*`(`^`(2, `/`(1, 2)), `*`(`^`(`/`(`*`(alpha, `*`(E, `*`(`^`(R[SE], 2)))), `*`(`^`(R[Ss], 2), `*`(epsilon, `*`(sigma)))), `/`(1, 4))))))](images/p661_11.gif)