| > | restart:#"m13_p57" |
| > | read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):with(plots):with(RealDomain): |
En un recinto grande con paredes a 20 ºC en el que se ha hecho el vacÃo, se mantiene colgado en medio un disco delgado de 0,1 m de radio con una resistencia eléctrica embutida que disipa 50 W. El disco tiene un recubrimiento metalizado cuya emisividad es de 0,1. Suponiendo térmicamente despreciable la conexión alámbrica, se pide:
a) Temperatura que alcanza el disco.
b) Temperatura que alcanzarÃa otro disco semejante al anterior y dispuesto paralelamente y concéntrico a 0,1 m de distancia del disco calefactor.
c) Resolver el apartado anterior pero cuando la separación tiende a cero.
dat:=[R=0.1*m_,T0=(20+273.15)*K_,Wdot=50*W_,epsilon=0.1,L=0.1*m_];dat:=op(dat),Const,SI2,SI1:h:='h':
| (1) |
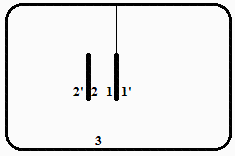
a) Temperatura que alcanza el disco.
Al ser el recinto grande, se comporta como cuerpo negro (si no lo fuera, las múltiples reflexiones de una parte a otra de las paredes lo harÃan comportarse como absorbedor total).
Se supone que emite por igual por ambas caras del disco (el área total será 2*Pi*R^2).
| > | eqBE:=C*dT/dt=Wdot-Qwall;eqBE:=0=Wdot-epsilon*A*sigma*(T^4-T0^4);eqA:=A=2*Pi*R^2;;eqA_:=evalf(subs(dat,%));eqBE_:=subs(eqA_,dat,SI0,eqBE);T_:=fsolve(%,T=100..1000)*K_;'T_'=TKC(%); |
| (2) |
i.e. para evacuar 50 W el disco ha de alcanzar 347 ºC.
b) Temperatura que alcanzarÃa otro disco semejante al anterior y dispuesto paralelamente y concéntrico a 0,1 m de distancia del disco calefactor.
Como intervienen más de dos superficies no negras, hay que recurrir al método de las exitancias, cuyo planteamiento es el siguiente.
Sean 1 y 1' las caras del disco calefactado, y 2 y 2' las caras del otro disco, con 1 y 2 enfrentadas
| > | eq1:=(M1-M1bb)/((1-epsilon1)/(A1*epsilon1))=A1*F12*(M2-M1)+A1*F13*(M3-M1);eq2:=(M2-M2bb)/((1-epsilon2)/(A2*epsilon2))=A2*F21*(M1-M2)+A2*F23*(M3-M2);eq3:=(M1-M1bb)/((1-epsilon1)/(A1*epsilon1))=-Wdot+epsilon1*A1*(M1bb-M3);eq4:=(M2-M2bb)/((1-epsilon2)/(A2*epsilon2))=epsilon2*A2*(M2bb-M3);eqM3:=M3=sigma*T0^4;eqM3_:=subs(dat,%);eqF12:=F12=1+1/(2*r^2)*(1-sqrt(4*r^2+1));eqr:=r=R/L;eqr_:=subs(dat,%);F12_:=subs(eqr_,rhs(eqF12));eqF13:=F13=1-F12;F13_:=1-F12_;eqA:=A=Pi*R^2;;eqA_:=evalf(subs(dat,%)); |
| (3) |
Se trata de 4 cuaciones (eq1,eq2,eq3,eq4) con 4 incógnitas (M1,M1bb,M2,M2bb), cuya solución es:
| > | datee:=epsilon1=subs(dat,epsilon),epsilon2=subs(dat,epsilon);sol4:=solve({eq1,eq2,eq3,eq4},{M1,M1bb,M2,M2bb}):sol4_:=subs(datee,A1=A,A2=A,eqA_,F21=F12,F23=1-F12,F12=F12_,F13=F13_,eqM3_,dat,sol4);eqT:=T^4=Mbb/sigma;T1_:=evalf(subs(sol4_,dat,SI0,(M1bb/sigma)^(1/4)))*K_;'T1_'=TKC(%);T2_:=evalf(subs(sol4_,dat,SI0,(M2bb/sigma)^(1/4)))*K_;'T2_'=TKC(%);eq12:=Q12=A1*F12*(M2-M1);subs(sol4_,A1=rhs(eqA_),F12=F12_,dat,%); |
| (4) |
i.e. con el disco próximo, el calefactor ha de ponerse a 348 ºC (1 K más que antes porque el otro disco apantalla un poco), mientras que el disco de al lado se pone a 47 ºC con los 7 W que recibe del disco calefactor (nótese que, aunque usamos el sÃmbolo Q como si fuera calor, en realidad es el intercambio radiativo neto, que podrÃa ser distinto de 0 incluso con T1=T2 si tienen distinta emisividad).
c) Resolver el apartado anterior pero cuando la separación tiende a cero.
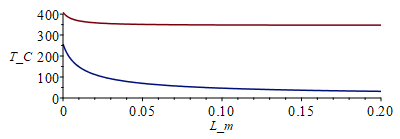
En función de la separación entre discos:
| > | F12_:=subs(r=R/L_m,dat,SI0,rhs(eqF12));F13_:=1-F12_;sol4_:=subs(datee,A1=A,A2=A,eqA_,F21=F12,F23=1-F12,F12=F12_,F13=F13_,eqM3_,dat,SI0,sol4):T1_:=subs(sol4_,dat,SI0,(M1bb/sigma)^(1/4)):T2_:=subs(sol4_,dat,SI0,(M2bb/sigma)^(1/4)):plot([T1_-273,T2_-273],L_m=0..0.2,T_C=0..400);F12_T1_T2_veryfar:=evalf(subs(L_m=1e3,[F12_,T1_-273.15,T2_-273.15]));F12_T1_T2_nearcontact:=evalf(subs(L_m=1e-6,[F12_,T1_-273,T2_-273])); |
 |
|
| (5) |
i.e. cuando los dos discos están prácticamente juntos, el calefactor ha de alcanzar 409 ºC, bastante más que cuando estaba solo (que quedaba a 347 ºC), debido al apantallamiento que sufre por la presencia del otro, que alcanzarÃa 258 ºC. Nótese que, con este modelo radiativo puro no puede representarse el caso de los dos discos en contacto, donde la conductividad harÃa que se igualasen las temperaturas y quedase el conjunto como un único disco (a 347 ºC).
| > |