| > | restart:#"m13_p32" |
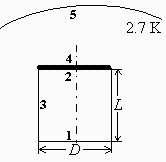
Consider a cylindrical evacuated enclosure 0.5 m in diameter and 0.5 m in length. One of the bases is a thin plate exposed on the outside to the 2.7 K of outer-space background radiation, while the other surfaces are kept at constant temperature. Find:
a) All the view factors implied.
b) All the heat flows at the steady state, assuming black-body surfaces, with 400 K for the temperature-regulated surfaces.
c)Same as before, but considering an emissivity =0.5 for the surfaces at 400 K.
d) The same, but releasing the fixed temperature condition at the base, which should be considered now as an insulated re-radiating black-body surface.
Data:
| > | read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):with(RealDomain): |
| > | dat:=[D=0.5*m_,L=0.5*m_,T5=2.7*K_,T1=400*K_,T3=400*K_,epsilon=0.5]; |
| (1) |
| > | dat:=op(dat),Const,SI2,SI1: |
a) All the view factors implied.
Each base plate has a face area A1=A2=D12/4=0.52/4=0.196 m2, and the lateral area is A3=DL=0.5•0.5=0.875 m2.
We must assume that all surfaces are opaque isothermal and diffuse. The view factor between the circular plates can be found on View factor tabulations.
| > | F12:=(x-y)/2;y:=sqrt(x^2-4*(r2/r1)^2);x:=1+1/r1^2+(r2/r1)^2;r1:=D/(2*L);r2:=D/(2*L);F12:=subs(dat,F12);F21:=F12;eqClose:=F11+F12+F13=1;F11:=0;F13:=F23;F23:=1-F12;eqRecpr:=A1*'F13'=A3*F31;F31:=F32;F32:=A1*'F13'/A3;A1:=Pi*D^2/4;A1:=evalf(subs(dat,%));A2:=A1;A3:=Pi*D*L;A3:=evalf(subs(dat,%));F13:=subs(dat,F13);F23:=subs(dat,F23);F31:=subs(dat,F31);F32:=subs(dat,F32);eqClos:='F31+F32+F33=1';F33:=1-F31-F32; |
| (2) |
b) All the heat flows at the steady state, assuming black-body surfaces, with 400 K for the temperature-regulated surfaces.
Surfaces 1 and 3 are maintained at 400 K, and the exposed plate only sees a black-body at 400 K from its face 2, and a black-body at 2.7 K from its face 4, so that its thermal balance at the steady state is:
| > | eqEB:=0=Q[13,2]-Q[4,5];eqEB:=0=A2*sigma*(T13^4-T2^4)-A2*sigma*(T4^4-T5^4);T4:=T2;T2:=((T13^4+T5^4)/2)^(1/4);T2_:=subs(T13=T1,dat,SI0,%)*K_;'T2_'=TKC(%);Q[13,2]:=subs(T13=T1,T2=T2_,dat,A2*sigma*(T13^4-T2^4));Q[4,5]:=subs(T13=T1,T4=T2_,dat,A2*sigma*(T4^4-T5^4));Q[1,2]:='Q[13,2]*F21';Q[1,2]:=Q[1,2];Q[3,2]:='Q[13,2]*F23';Q[3,2]:=Q[3,2]; |
| (3) |
i.e. plate 2 reaches 336 K, receiving 142 W from inside (24 W from 1 and 118 W from 3), and sending the same 142 W outside. There is no heat transfer between surfaces 1 and 3, being at the same temperature.
c) Same as before, but considering an emissivity =0.5 for the surfaces at 400 K.
This case corresponds to an enclosure with only two isothermal surfaces: A[1+3]=0.196+0.875=1.07 m2, and A[2]=0.196 m2, with one of them non-concave, F[2,1+3]=1, and thence:
| > | T2:='T2':Q[2,13]:='A2'*sigma*(T2^4-T13^4)/(1/epsilon2+('A2/A13')*(1/epsilon13-1));A13:='A1+A3';Q_[2,13]:=subs(T13=T1,epsilon2=1,epsilon13=epsilon,dat,Q[2,13]); |
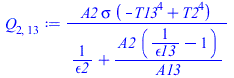 |
|
| (4) |
with the same type of energy balance:
| > | eqEB:=0='Q[13,2]-Q[4,5]';eqEB:=0='-Q[2,13]'-'A2'*sigma*(T2^4-T5^4);eqEB_:=subs(dat,0=-Q_[2,13]-A2*sigma*(T2^4-T5^4));T2_:=solve(%,T2)[1];Q[13,2]:=subs(T2=T2_,dat,-Q_[2,13]); |
| (5) |
i.e., now T2=328 K and Q[2,13]=130 W (against the 336 K and 142 W obtained with the black-body hypothesis, showing again that when two surfaces widely different in size exchange radiation, the thermo-optical properties of the larger are irrelevant.
d) The same, but releasing the fixed temperature condition at the base, which should be considered now as an insulated re-radiating black-body surface.
This is a general case with opaque diffuse surfaces, which must be solved in terms of the general radiative balance at each surface (exitance method in lumped network model):
| > | Q[j,net]:=Aj*(Ej-Mj);Q[j,net]:=Sum(Ai*Fij*(Mi-Mj),i=1..N);eq1:='A2*F21*(M2-M1)+A3*F32*(M3-M1)=0';eq2:='A1*F12*(M1-M2)+A3*F32*(M3-M2)'='A2'*sigma*(T4^4-T5^4);eq3:='A1*F13*(M1-M3)+A2*F23*(M2-M3)=A3*epsilon3*(M3-M3bb)/(1-epsilon3)';M1:=sigma*T1new^4;M2:=sigma*T2^4;M3bb:=sigma*T3^4;sol_:=fsolve(subs(epsilon3=epsilon,dat,SI0,{eq1,eq2,eq3}),{T1new,T2,M3},{T1new=100..400,T2=100..400}):T1new_:=subs(sol_,T1new)*K_;T2_:=subs(sol_,T2)*K_;M3_:=subs(sol_,M3)*W_/m_^2; |
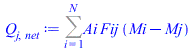 |
|
| (6) |
i.e. the reradiating surface 1 attains T1=380 K, while the exposed plate 2 reaches T2=326 K. Substituting those values, the energy balances show all the heat flows implied (really net radiation exchange, since it is inappropriate to talk about heat transfer between two separate bodies in the presence of others):
| > | eq0_:='A2*F21*(M2-M1)'=subs(sol_,dat,SI0,A2*F21*(M2-M1))*W_/m_^2;eq1_:=subs(sol_,dat,SI0,eq1);eq2_:=subs(sol_,dat,SI0,eq2)*W_/m_^2;eq3_:=subs(epsilon3=epsilon,sol_,dat,SI0,eq3)*W_/m_^2; |
| (7) |
i.e. there must be an energy source of 125 W at surface 3 (the lateral wall kept at 400 K), to compensate the net radiative exchange with surface 1 (which gets 18 W) and surface 2 (which gets 107 W), being both colder. The energy balance of the upper plate shows that it gets 18 W from the bottom base, 107 W from the lateral wall, and delivers the total 125 W to deep space.
| > |