| > | restart:#"m11_p92" |
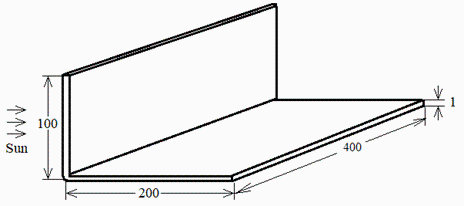
Se quiere estudiar el campo de temperaturas en un apéndice de un satélite geoestacionario, cuyo modelo simplificado puede aproximarse por una placa de aluminio A7075 de LxLyLz=300×400×1 mm3 doblada en ángulo recto a 1/3 de Lx y expuesta al sol por la cara menor como se muestra en la figura. Despreciando las interacciones térmicas con el resto del satélite y suponiendo que radia como cuerpo negro, se pide:
a) Temperatura media estacionaria que alcanzaría la placa (modelo isotermo, i.e. un solo nodo), despreciando la re-radiación entre elementos.
b) Temperaturas medias estacionarias que alcanzarían ambos trozos planos (modelo de dos nodos), despreciando la re-radiación entre elementos.
c) Temperaturas medias estacionarias que alcanzarían los tres trozos planos (el vertical, y los dos que se obtienen dividiendo por la mitad el horizontal, i.e. modelo de tres nodos), despreciando la re-radiación entre elementos.
d) Considerando un modelo unidimensional (Ly∞), calcular analíticamente el perfil de temperaturas T(x) a lo largo de toda la placa*, teniendo en cuenta la conducción y aproximando la radiación por =hdA(TT∞) con h=1 W/(m2·K).
e) Resolver numéricamente el apartado anterior.
f) Para simular el enfriamiento radiativo por los bordes, que están menos apantallados que el centro, resolver el modelo bidimensional, teniendo en cuenta la conducción y aproximando la radiación por =hdA(TT∞) con W/(m2·K), con el origen de coordenadas (x,y) en el centro de la unión (i.e. emitiéndose en los extremos un 40 % más).
g) Evolución de las temperaturas al entrar en eclipse.
*Para facilitar la presentación gráfica de resultados, puede usarse la variable s (0≤s≤Lx) correspondiente al camino a lo largo de la placa, pero teniendo en cuenta en los modelos que la placa está doblada.
Datos:
| > | read"../therm_eq.m":read"../therm_proc.m":with(therm_proc): |
| > | su:="Al-7075":dat:=[Lx=0.3*m_,Ly=0.4*m_,Lz=1e-3*m_,Lxh=0.2*m_,Lxv=0.1*m_,E=1360*W_/m_^2,Tinf=2.7*K_,her=1*W_/(m_^2*K_),alpha=1,epsilon=1]; |
Tomaremos las siguientes propiedades para el aluminio:
| > | dat:=op(dat),get_sol_data(su),Const,SI2,SI1:A7075_rho_c_k_alpha_epsilon:=subs(dat,[rho,c,k,alpha,epsilon]); |
a) Temperatura media estacionaria que alcanzaría la placa (modelo isotermo, i.e. un solo nodo), despreciando la re-radiación entre elementos..
Como es habitual, en estos cálculos aproximados, en órbita geoestacionaria despreciamos los efectos térmicos de la Tierra.
Consideramos rayos solares paralelos, y despreciaremos la Tinf frente a las temperaturas esperadas.
Sea Lxh la parte horizontal (0,2 m) y Lxv la vertical (0,1 m), soleada.
Si toda la placa está a T1, y no se considera la re-radiación, el balance energético es:
| > | eqBE:=m*c*dT/dt=Qin-Qout;Qin:=alpha*E*Lxv*Ly;Qin_:=subs(dat,%);Qout:=epsilon*2*Lx*Ly*sigma*(T1^4-Tinf^4);T1=((alpha*E*Lxv*Ly)/(2*Lx*Ly*epsilon*sigma))^(1/4);T1_:=solve(subs(dT=0,dat,SI0,eqBE),T1)[1]*K_;'T1_'=TKC(%); |
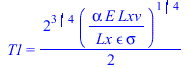 |
|
| (1) |
i.e. la placa absorbe 54 W de radiación solar, y, si emitiera por toda el área al espacio de fondo (i.e. sin re-radiación) quedaría a -22 ºC.
Si se tuviera en cuenta la re-radiación quedaría un poco más caliente por el apantallamiento radiativo.
Sea 1 el tramo vertical y 2 el horizontal. El factor de vista de la cara vertical a la horizontal, F12, se obtine de la Tabla de factores de vista (¡ojo! que la expresión de allí nos da el recíproco):
| > | Qout:=(2-F21)*Lxh*Ly*sigma*(T1^4-Tinf^4)+(2-F12)*Lxv*Ly*sigma*(T1^4-Tinf^4);F21:=(1/(Pi*w))*(w*arctan(1/w)+h*arctan(1/h)-sqrt(w^2+h^2)*arctan(1/sqrt(w^2+h^2))+ln(a*b^(w^2)*c^(h^2))/4);a:=(1+w^2)*(1+h^2)/(1+w^2+h^2);b:=w^2*(1+w^2+h^2)/((1+w^2)*(w^2+h^2));c:=h^2*(1+h^2+w^2)/((1+h^2)*(h^2+w^2));eqh:=h=Lxv/Ly;eqh_:=subs(dat,%);eqw:=w=Lxh/Ly;eqw_:=subs(dat,%);F21_:=evalf(subs(eqh_,eqw_,F21));F12=A2*'F21'/A1;F12_:=subs(dat,Lxh*F21_/Lxv);F12:='F12':F21:='F21':T1_:=solve(subs(dT=0,F12=F12_,F21=F21_,dat,SI0,eqBE),T1)[1]*K_;'T1_'=TKC(%);c:='c': |
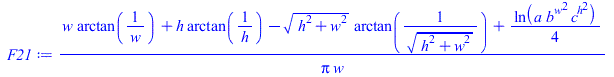 |
|
| (2) |
i.e. el angular quedaría a -14 ºC en vez de los -22 ºC antes calculados, debido a que al tener una superficie cóncava emite menos al espacio de fondo.
Nótese que no se pone epsilon por incompatibilidad de modelos.
b) Temperaturas medias estacionarias que alcanzarían ambos trozos planos (modelo de dos nodos), despreciando la re-radiación entre elementos.
Sea T1 la del nodo vertical y T2 la del horizontal. Sus balances energéticos son:
| > | eqBE1:=m1*c1*dT1/dt=Qs1-Qrad1-Qcond1;eqBE2:=m2*c2*dT2/dt=Qcond1-Qrad2;eqBE1:=0=Qin-epsilon*2*Lxv*Ly*sigma*(T1^4-Tinf^4)-k*Ly*Lz*(T1-T2)/(Lx/2);eqBE2:=0=k*Ly*Lz*(T1-T2)/(Lx/2)-epsilon*2*Lxh*Ly*sigma*(T2^4-Tinf^4);eqBE1_:=subs(dat,SI0,eqBE1);eqBE2_:=subs(dat,SI0,eqBE2);Ts_:=op(fsolve({eqBE1_,eqBE2_},{T1,T2},T1=200..400)):T1_:=subs(Ts_,T1)*K_;'T1'=TKC(%);T2_:=subs(Ts_,T2)*K_;'T2'=TKC(%);Qrad1_:=subs(dat,epsilon*2*Lxv*Ly*sigma*(T1_^4-Tinf^4));Qcond1_:=subs(dat,k*Ly*Lz*(T1_-T2_)/(Lx/2));Qrad2_:=subs(dat,epsilon*2*Lxh*Ly*sigma*(T2_^4-Tinf^4)); |
| (3) |
i.e. la parte vertical (1) quedaría a 15 ºC y la horizontal (2) queda a -49 ºC, en lugar de ambas a -22 ºC. La 1 absorbe 54 W del Sol, y emite 31 W al vacío y conduce 23 W (netos) a la 2, que los elimina al vacio.
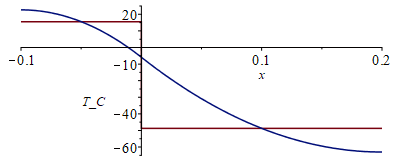
Este sencillo modelo de dos nodos puede refinarse mucho sin necesidad de mejorar la discretización, sustituyendo esta solución en escalón por un ajuste polinómico suave que empalme vien en el doblez (T1=T2 y dT1/dx=dT2/dx en x=0), que pase por los nodos a las temperaturas antes calculadas, y que acabe con pendiente nula en los extremos (pérdidas laterales despreciables en el espesor de la placa):
| > | T1x:=a1*x^2+b1*x+c1;T2x:=a2*x^2+b2*x+c2;eqs:=[subs(x=-0.1,diff(T1x,x))=0,subs(x=-0.05,T1x)=T1_/K_,subs(x=0,T1x)=subs(x=0,T2x),subs(x=0,diff(T1x,x))=subs(x=0,diff(T2x,x)),subs(x=0.1,T2x)=T2_/K_,subs(x=0.2,diff(T2x,x))=0];sol_:=op(solve(eqs,[a1,b1,c1,a2,b2,c2]));p1:=piecewise(x<0,T1_/K_,T2_/K_):p2:=piecewise(x<0,subs(sol_,T1x),subs(sol_,T2x)):plot([p1-273,p2-273],x=-0.1..0.2, T_C=-65..25); |
 |
Si no se desprecia la re-radiación:
| > | eqBE1:=0=Qin-(2-F12)*Lxv*Ly*sigma*(T1^4-Tinf^4)-F12*Lxv*Ly*sigma*(T1^4-T2^4)-k*Ly*Lz*(T1-T2)/(Lx/2);eqBE2:=0=k*Ly*Lz*(T1-T2)/(Lx/2)+F12*Lxv*Ly*sigma*(T1^4-T2^4)-(2-F21)*Lxh*Ly*sigma*(T2^4-Tinf^4);eqBE1_:=subs(F12=F12_,dat,SI0,eqBE1);eqBE2_:=subs(F12=F12_,F21=F21_,dat,SI0,eqBE2);Ts_:=op(fsolve({eqBE1_,eqBE2_},{T1,T2},T1=200..400)):T1_:=subs(Ts_,T1)*K_;'T1'=TKC(%);T2_:=subs(Ts_,T2)*K_;'T2'=TKC(%);Qrad1inf_:=subs(dat,(2-F12_)*Lxv*Ly*sigma*(T1_^4-Tinf^4));Qrad12_:=subs(dat,F12_*Lxv*Ly*sigma*(T1_^4-T2_^4));Qcond1_:=subs(dat,k*Ly*Lz*(T1_-T2_)/(Lx/2));Qrad2_:=subs(F21=F21_,dat,(2-F21)*Lxh*Ly*sigma*(T2_^4-Tinf^4)); |
| (4) |
i.e. la parte vertical quedaría a 23 ºC en vez de a 15 ºC, y la horizontal a -38 ºC en vez de a -49 ºC. La 1 absorbe 54 W del Sol, y cede 29 W al vacío, y 25 W a la 2 (3 W por radiación neta y 22 W por conducción).
c) Temperaturas medias estacionarias que alcanzarían los tres trozos planos (el vertical, y los dos que se obtienen dividiendo por la mitad el horizontal, i.e. modelo de tres nodos), despreciando la re-radiación entre elementos.
Sea T1 la vertical, T2 la horizontal contigua, y T3 la horizontal alejada. Sus balances energéticos son:
| > | eqBE1:=m1*c1*dT1/dt=Qs1-Qrad1-Qcond1;eqBE2:=m2*c2*dT2/dt=Qcond1-Qrad2-Qcond3;eqBE3:=m3*c3*dT3/dt=Qcond3-Qrad3;eqBE1:=0=Qin-epsilon*2*Lxv*Ly*sigma*(T1^4-Tinf^4)-k*Ly*Lz*(T1-T2)/(Lxh/2);eqBE2:=0=k*Ly*Lz*(T1-T2)/(Lxh/2)-epsilon*Lxh*Ly*sigma*(T2^4-Tinf^4)-k*Ly*Lz*(T2-T3)/(Lxh/2);eqBE3:=0=k*Ly*Lz*(T2-T3)/(Lxh/2)-epsilon*Lxh*Ly*sigma*(T3^4-Tinf^4);eqBE1_:=subs(dat,SI0,eqBE1);eqBE2_:=subs(dat,SI0,eqBE2);eqBE3_:=subs(dat,SI0,eqBE3);Ts_:=op(fsolve({eqBE1_,eqBE2_,eqBE3_},{T1,T2,T3},T1=200..400)):T1_:=subs(Ts_,T1)*K_;'T1'=TKC(%);T2_:=subs(Ts_,T2)*K_;'T2'=TKC(%);T3_:=subs(Ts_,T3)*K_;'T3'=TKC(%);Qrad1inf_:=subs(dat,2*Lxv*Ly*sigma*(T1_^4-Tinf^4));Qcond1_:=subs(dat,k*Ly*Lz*(T1_-T2_)/(Lxh/2));Qrad2_:=subs(dat,Lxh*Ly*sigma*(T2_^4-Tinf^4));Qcond3_:=subs(dat,k*Ly*Lz*(T2_-T3_)/(Lxh/2));Qrad3_:=subs(dat,Lxh*Ly*sigma*(T3_^4-Tinf^4)); |
| (5) |
i.e. la vertical quedaría a T1=11 ºC, la horizontal contigua a T2=-35 ºC, y la horizontal lejana a T3=-55 ºC. De los 54 W que absorbe la 1, emite 30 W al vacío y conduce los otros 25 W hacia la 2, lacual radia 15 W y conduce 10 W hacia la 3, que los radia.
d) Considerando un modelo unidimensional (Ly∞), calcular analíticamente el perfil de temperaturas T(x) a lo largo de toda la placa*, teniendo en cuenta la conducción y aproximando la radiación por =hdA(TT∞) con h=1 W/(m2·K).
El balance energético de un elemento diferencial da lugar, con esta simplificación, a una ecuación diferencial ordinaria integrable:
| > | eqBE:=rho*c*diff(T(x,t),t)=k*diff(T(x,t),x,x)+phi;eqBE:=0=k*A*diff(T(x),x,x)+E*p-h*p*(T(x)-Tinf); |
| (6) |
Como solo recibe sol en el tramo vertical, hay que separar en dos trozos, el vertical (luego cambiaremos de variable; sea ahora 0<x<Lxv), y el horizontal con 0<x<Lxh.
| > | eqBEv:=eqBE;eqBEh:=subs(E=0,eqBE);eqm:=m=sqrt(h*p/(k*A));eqm:=m=sqrt(her*2*Ly/(k*Ly*Lz));eqm_:=m=evalf(subs(dat,SI0,rhs(%)))/m_; |
| (7) |
cuyas soluciones analíticas se pueden tomar de la Tabla 4 de Heat conduction.
Para el trama horizontal:
| > | eqTh:=(T(x)-Tinf)/(T0h-Tinf)=cosh(m*(Lxh-x))/cosh(m*Lxh);eqQ0h:=Q0=(T0h-Tinf)*sqrt(phkA)*tanh(m*Lxh);eqphkA:=phkA=2*Ly*her*k*Ly*Lz; |
| (8) |
Para el tramo vertical:
| > | eqTv:=(T(x)-Tinf)/(T0v-Tinf)=cosh(m*(Lxv-x))/cosh(m*Lxv)+phi/(k*m^2*(T0v-Tinf));eqQ0v:=Q0=(T0v-Tinf)*sqrt(phkA)*tanh(m*Lxv);eqphi:=phi=E*p/(2*A);eqphi:=phi=E/Lz;eqphi_:=subs(dat,eqphi); |
| (9) |
igualando las temperaturas y los flujos de calor en la unión:
| > | eqTs:=evalf(subs(x=0,Tinf+(T0h-Tinf)*rhs(eqTh)))=evalf(subs(x=0,Tinf+(T0v-Tinf)*rhs(eqTv)));eqQs:=rhs(eqQ0h)+rhs(eqQ0v)=0;eqTs_:=evalf(subs(eqm_,eqphi_,dat,SI0,eqTs));eqQs_:=evalf(subs(eqm_,eqphkA,dat,SI0,eqQs));sol_:=op(solve([eqTs_,eqQs_],[T0h,T0v]));T0h_:=subs(sol_,T0h)*K_;'T0h_'=TKC(%);T0v_:=subs(sol_,T0v)*K_;'T0v_'=TKC(%); |
| (10) |
cuya representación gráfica es:
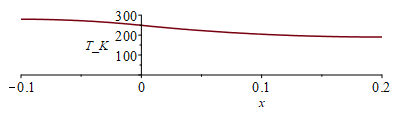
| > | Th_:=evalf(subs(T0h=T0h_,eqm_,dat,SI0,Tinf+(T0h-Tinf)*rhs(eqTh)));ThL_:=evalf(subs(x=Lxh,dat,SI0,Th_))*K_;Q0h_:=evalf(subs(x=0,dat,SI0,k*Ly*Lz*diff(Th_,x)))*W_;Tv_:=evalf(subs(T0v=T0v_,eqm_,eqphi,dat,SI0,Tinf+(T0v-Tinf)*rhs(eqTv)));TvL_:=evalf(subs(x=Lxv,dat,SI0,Tv_))*K_;Q0v_:=evalf(subs(x=0,dat,SI0,k*Lz*Ly*diff(Tv_,x)))*W_;Ts_:=piecewise(x<0,subs(x=-x,Tv_),Th_);plot(Ts_,x=-0.1..0.2,T_K=0..300);plot(Ts_-273,x=-0.1..0.2,T_C=-90..10); |
![Typesetting:-mprintslash([Ts_ := PIECEWISE([`+`(682.7000008, `-`(`*`(403.2628388, `*`(cosh(`+`(`-`(.3863337045), `-`(`*`(3.863337045, `*`(x))))))))), `<`(x, 0)], [`+`(2.7, `*`(187.4665082, `*`(cosh(`+...](images/p921_105.gif) |
|
 |
|
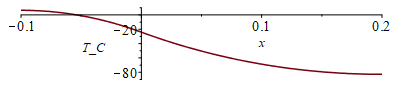 |
i.e. el extremo soleado quedaría a 279 K (6 ºC), el canto común a T0h=249 K (-24 ºC), y el extremo en sombra a 190 K (-83 ºC), pasando 33 W del tramo soleado al de sombra (por conducción). El punto de inflexión de la curva T(x) ocurre en el punto de unión (donde el flujo de calor por conducción es máximo).
No sabemos si este modelo de coeficiente convectivo para simular la radiación será válido, pero parece razonable (la linealización del término radiativo da h=4*sigma*Tmean^3). Para comparar, el modelo de dos nodos sin re-radiación daba Tmedia=15 ºC en la zona soleada y Tmedia=-49 ºC en la horizontal.
e) Resolver numéricamente el apartado anterior.
Se trata de poder comparar la solución numérica con la analítica. En lugar de resolver el caso estacionario (una EDO), resolveremos el transitorio (una EDP), que es de mayor aplicación pues permite usar términos no lineales.
Solución numérica. Sea N el número de tramos en que dividimos la chapa completa (N+1 puntos): 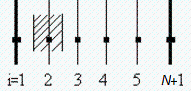 . Desde i=1 hasta i=N/3+1 está soleado y el resto no.
. Desde i=1 hasta i=N/3+1 está soleado y el resto no.
El balance energético de un elemento discreto es:
| > | eqBE:=rho*c*A*Dx*(T[j+1,i]-T[j,i])/Dt=k*A*(T[j,i+1]-T[j,i])/Dx-k*A*(T[j,i]-T[j,i-1])/Dx+phi*A*Dx-p*h*Dx*(T[j,i]-Tinf);eqTi:=T[j+1,i]=T[j,i]+(Dt/(rho*c))*(k*(T[j,i+1]-2*T[j,i]+T[j,i-1])/Dx^2+phi-(p*h/A)*(T[j,i]-Tinf));eqT1:=T[j+1,1]=T[j,2];eqTN1:=T[j+1,N+1]=T[j,N]; |
![Typesetting:-mprintslash([eqTi := T[`+`(j, 1), i] = `+`(T[j, i], `/`(`*`(Dt, `*`(`+`(`/`(`*`(k, `*`(`+`(T[j, `+`(i, 1)], `-`(`*`(2, `*`(T[j, i]))), T[j, `+`(i, `-`(1))]))), `*`(`^`(Dx, 2))), phi, `-`(...](images/p921_110.gif) |
|
| (11) |
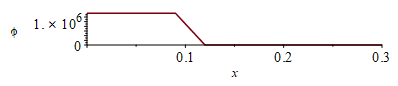
Tomaemos una Tinicial=15 ºC, aunque es irrelevante para llegar al estacionario. Como la absorción solar, phi=E/Lz, es discontinua, si no se quiere suavizar conviene una discretización fina.
| > | o:=273.15:T:='T':N:=10;Dx:=evalf(subs(dat,SI0,Lx/N));tsim:=7500;M:=16000/16;Dt:=tsim/M;eqFo:='Fo=k*Dt/(rho*c*Dx^2)';Fo:=subs(dat,SI0,rhs(%));p_:=subs(dat,SI0,2*Ly);h_:=subs(dat,SI0,her);k_:=subs(dat,SI0,k);rho_:=subs(dat,SI0,rho);c_:=subs(dat,SI0,c);A_:=subs(dat,SI0,Ly*Lz);Tinf_:=subs(dat,SI0,Tinf);T0_:=subs(dat,SI0,T0);phi_:=subs(dat,SI0,rhs(eqphi_));for i from 1 to N+1 do if i<N/3+1 then phi[i]:=phi_;else phi[i]:=0;end if;od;T:=Matrix(1..M+1,1..N+1,T0_):plot([seq([(i-1)*Dx,phi[i]],i=1..N+1)],x=0..0.3,phi=0..phi_); |
 |
y la evolución T(t,x) es:
| > | for j from 1 to M do T[j+1,1]:=T[j,2];T[j+1,N+1]:=T[j,N];for i from 2 to N do T[j+1,i]:=T[j,i]+(Dt/(rho_*c_))*(k_*(T[j,i+1]-2*T[j,i]+T[j,i-1])/Dx^2+phi[i]-(p_*h_/A_)*(T[j,i]-Tinf_));od:od:i:='i':j:='j':Mjump:=50:sx:=seq([seq([i*Dx,T[1+j_*Mjump,i]-o],i=1..N+1)],j_=0..M/Mjump):plot([sx],x_m=0..0.3,T_C=-90..50);st:=seq([seq([j*Dt,T[j,i]-o],j=1..M+1)],i=1..N+1):plot([st],t_s=0..tsim,T_C=-90..50); |
 |
|
 |
Y si comparamos el último resultado con el modelo analítico y el modelo de tres nodos:
| > | Tlast_K:=seq(T[M,i],i=1..N+1);T:='T':pl:=seq([-0.1+(i-1)*Dx,Tlast_K[i]-o],i=1..N+1):pl3:=piecewise(x<0,T1_/K_-o,x>subs(dat,SI0,Lxh/2),T3_/K_-o,T2_/K_-o);plot([[pl],Ts_-o,pl3],x=-0.1..0.2,T_C=-90..11); |
![Typesetting:-mprintslash([pl3 := PIECEWISE([10.9756018, `<`(x, 0)], [-54.6541325, `<`(.1000000000, x)], [-35.3664008, otherwise])], [piecewise(`<`(x, 0), 10.9756018, `<`(.1000000000, x), -54.6541325, ...](images/p921_133.gif) |
|
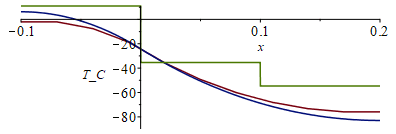 |
vemos que la concordancia entre este modelo numérico y el analítico es buena pese a usar solo 10 tramos en la discretización.
f) Para simular el enfriamiento radiativo por los bordes, que están menos apantallados que el centro, resolver el modelo bidimensional, teniendo en cuenta la conducción y aproximando la radiación por =hdA(TT∞) con W/(m2·K), con el origen de coordenadas (x,y) en el centro de la unión (i.e. emitiéndose en los extremos un 40 % más).
Se ha resuelto en Matlab y el resultado se muestra a continuación: a) valores de h(xy) tomados (la línea roja es la charnela); b) T(z,y) en el plano abatido; c) valores de T en la configuración real.
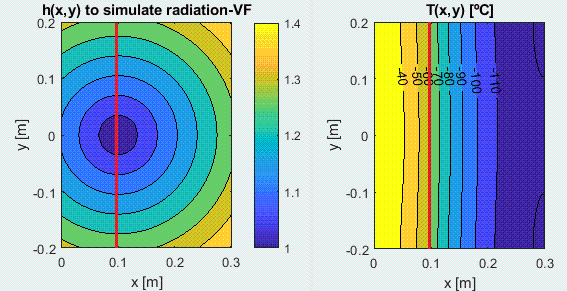
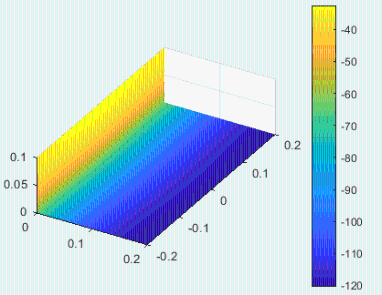
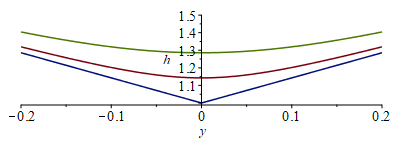
Como era de esperar, al incrementar h (más pérdidas por radiación equivalente) disminuyen las temperaturas, pero apenas se aprecian las variaciones transversales de temperatura T(y) pese a que por ejemplo en la charnela la h varía de h=1 W/(m2·K) en el centro (y=0) a h=1.3 W/(m2·K) en los bordes (y+/-Ly/2). La explicación es que la gran conductividad (k) de la chapa tiende a uniformizar las temperaturas, i.e. la placa se comporta como si tuviese una h uniforme de valor h_medio=1.2 W/(m2·K).
| > | eqh:=h=1+sqrt(x^2+y^2)/(Lx+Ly);plot([seq(subs(x=xh,dat,SI0,rhs(eqh)), xh in [-Lxv,0,Lxh])],y=-0.2..0.2,h=1..1.5);h_mean:=Int(Int(h,y=-Ly/2..Ly/2),x=-Lxv..Lxh)/(Lx*Ly)=2*int(int(subs(dat,SI0,rhs(eqh)/(Lx*Ly)),x=-0.1..0.2),y=0..0.2); |
 |
|
![Typesetting:-mprintslash([h_mean := `/`(`*`(Int(Int(h, y = `+`(`-`(`*`(`/`(1, 2), `*`(Ly)))) .. `+`(`*`(`/`(1, 2), `*`(Ly)))), x = `+`(`-`(Lxv)) .. Lxh)), `*`(Lx, `*`(Ly))) = 1.202249986], [`/`(`*`(In...](images/p921_139.gif) |
(12) |
g) Evolución de las temperaturas al entrar en eclipse.
Con el modelo 1D numérico (i.e. con h=1 W/(m2·K) constante):
| > | o:=273.15:T:='T':N:=10;Dx:=evalf(subs(dat,SI0,Lx/N));tsim:=7500;M:=16000/16;Dt:=tsim/M;eqFo:='Fo=k*Dt/(rho*c*Dx^2)';Fo:=subs(dat,SI0,rhs(%));p_:=subs(dat,SI0,2*Ly);h_:=subs(dat,SI0,her);k_:=subs(dat,SI0,k);rho_:=subs(dat,SI0,rho);c_:=subs(dat,SI0,c);A_:=subs(dat,SI0,Ly*Lz);Tinf_:=subs(dat,SI0,Tinf);T0_:=subs(dat,SI0,T0);T:=Matrix(1..M+1,1..N+1,T0_):for i from 1 to N+1 do T[1,i]:=Tlast_K[i];od: |
| (13) |
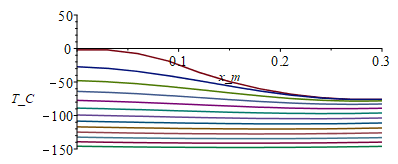
| > | o=0:for j from 1 to M do T[j+1,1]:=T[j,2];T[j+1,N+1]:=T[j,N];for i from 2 to N do T[j+1,i]:=T[j,i]+(Dt/(rho_*c_))*(k_*(T[j,i+1]-2*T[j,i]+T[j,i-1])/Dx^2-(p_*h_/A_)*(T[j,i]-Tinf_));od:od:i:='i':j:='j':Mjump:=10:sx:=seq([seq([(i-1)*Dx,T[1+j_*Mjump,i]-o],i=1..N+1)],j_=0..M/Mjump):plot([sx],x_m=0..0.3,T_C=-150..50);st:=seq([seq([j*Dt,T[j,i]-o],j=1..M+1)],i=1..N+1):plot([st],t_s=0..1000+0*tsim,T_C=-150..50); |
 |
|
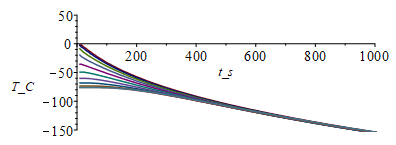 |
(a 75 s cada T(x)). Se ve que una chapa tan delgada, al entrar en eclipse se enfría muy deprisa (al cabo de los 2 min de penumbra ya estaría el extremo más calieente a unos -40 ºC.
Lo podíamos haber previsto analizando el modelo más simple de un solo nodo:
| > | T:='T':eqBE:=m*c*diff(T1(t),t)=-epsilon*2*Lx*Ly*sigma*(T1(t)^4-Tinf^4);eqm:=m=subs(dat,rho*Lx*Ly*Lz);eqBE_:=subs(eqm,dat,SI0,eqBE);sol_:=dsolve({eqBE_,T1(0)=250},T1(t),numeric);plot([seq(subs(sol_(i*100),[t,T1(t)]),i=0..40)],t=0..4000,T_K=0..250); |
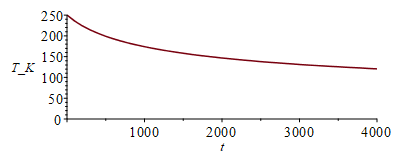 |
o incluso linealizándolo:
| > | eqBE:=m*c*dT/dt=-8*epsilon*Lx*Ly*sigma*Tm^3*(T-Tif);eqTm:=Tm=T0/2;tc:=m*c/(8*epsilon*Lx*Ly*sigma*Tm^3);tc_:=subs(eqm,eqTm,dat,%); |
| (14) |
i.e. el tiempo característico de enfriamiento hasta la mitad es de unos 2000 s, mientras que el tiempo en eclipse en GEO es de unos 70 min más 4 min de penumbra (en total casi 4500 s)
| > |