| > | restart:#"m09_p52" |
| > | read`../therm_chem.m`:with(therm_chem):with(therm_proc):interface(displayprecision=2): |
El óxido de dinitrógeno (óxido nitroso, N2O) se usa como propulsante en cohetes de líquidos y en híbridos, bien como oxidante con un combustible, bien como monopropulsante. Para un depósito de 1 m3, se pide:
a) Presión de almacenamiento en fase líquida a 0 ºC, 20 ºC y 40 ºC. Diagrama esquemático de la presión interior en función de la masa de N2O introducida (desde el estado inicial vacío), a T=20 ºC.
b) Entalpía y función de Gibbs de la reacción de descomposición del N2O en sus elementos, en condiciones estándar, interpretando los signos obtenidos. ¿Cómo se calcularía la función de Gibbs de formación estándar del N2O si faltara ese dato en las tablas de datos termoquímicos?
c) Temperatura adiabática de la descomposición completa del líquido saturado a 6 MPa.
d) Composición de equilibrio a esa temperatura y presión, suponiendo que también aparece NO.
Datos:
| > | su1:="N2O":su2:="N2":su3:="O2":dat:=[T10=(0+273.15)*K_,T12=(20+273.15)*K_,T14=(40+273.15)*K_,p1=6e6*Pa_]; |
Eqs. const.:
| > | Pdat:=get_liq_data(su1),get_gas_data(su1):get_pv_data(su1):NHdat:=get_gas_data(su2):Odat:=get_gas_data(su3):dat:=op(dat),op(subs(g=g0,[Const])),SI2,SI1: |
a) Presión de almacenamiento en fase líquida a 0 ºC, 20 ºC y 40 ºC. Diagrama esquemático de la presión interior en función de la masa de N2O introducida (desde el estado inicial vacío), a T=20 ºC.
Usaremos la correlación de Antoine para la presión de equilibrio líquido-vapor.
En la Tabla de líquidos, vemos que el N2O tiene Tb=184 K (-89 ºC) y Tcr=310 K (37 ºC), luego a 40 ºC no hay líquido (sería un gas supercrítico, cuya presión dependería de la masa de fluido introducida).
| > | p=p[v](T);p10:=subs(dat,evalf(subs(dat,pv(T10))));p12:=subs(dat,evalf(subs(dat,pv(T12))));p14:=subs(dat,evalf(subs(dat,pv(T14)))); |
i.e. a 0 ºC la presión de vapor es pv=3,14 MPa, a 20 ºC es pv=5,09 MPa, y a 40 ºC no se está definida (el valor de pv=7,74 MPa es la extrapolación de la ecuación de Antoine). Desde el estado de vacío, si se va introduciendo N2O a 20 ºC, al principio el estado será gaseoso, con p=rho/(RT) mientras se aproxime a gas ideal, hasta alcanzar la presión de vapor de 5,09 MPa en que dejará de aumentar la presión e irá aumentando la cantidad de líquido hasta que toda la masa interior fuese líquida y ya no se pudiera meter más (bueno, entraría algo más si la presión se aumentara mucho). La masa de N2O máxima, con el modelo de líquido perfecto sería el valor de la Tabla de líquidos, 1230 kg/m3, pero este valor es el del punto de ebullición normal, a 185 K (-89 ºC), siendo realmente de 785 kg/m3 a 20 ºC según los datos más precisos (NIST). Se podría haber usado el modelo de líquido dilatable lineal y calcular rho(T)=rho0(1-alpha·(T-Tb)), que con los datos de la Tabla de líquidos ya daría 911 kg/m3.
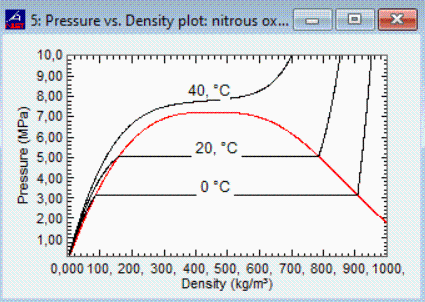
Fig. 1. Presión del N2O en función de la masa introducida en 1 m3, manteniendo la temperatura constante en 0 ºC, o 20 ºC, o 40 ºC (NIST).
Se podría haber usado el modelo de líquido dilatable lineal y calcular rho(T)=rho0(1-alpha·(T-Tb)), que con los datos de la Tabla de líquidos daría:
| > | eqDILAT:=rho(T)=rho[0]*(1-alpha*(T-T[b]));alpha:=2400e-6/K_:'alpha*1e6'=alpha*1e6;eqDILAT_:=rho[20ºC]=subs(Pdat,dat,rho*(1-alpha*(T12-T[b]))); |
Otro problema interesante sería e.g. determinar el nivel de líquido en un depósito de 1 m3 conteniendo e.g. 500 kg de N2O a 0 ºC, al ir aumentando la temperatura, y el resultado con los datos del NIST es:
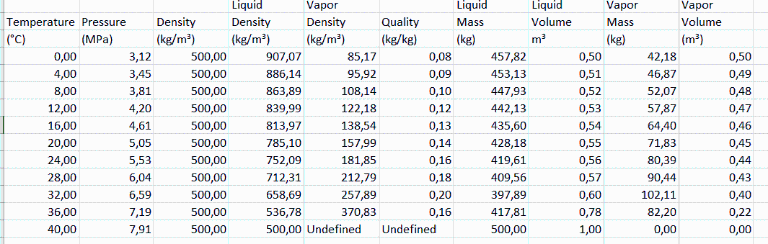
habiendo adscrito el estado superfluido a la columna de líquido. Como se aprecia en la Tabla, al principio hay equilibrio líquido-vapor, y al aumentar la T aumenta la presión; el volumen de líquido que a 0 ºC es 0,5 m3, va aumentando con la temperatura hasta ocupar todo el recipiente de 1 m3 cerca de la temperatura crítica (Tcr=36,37 ºC). El proceso sería un recta vertical en el diagrama de la Fig. 1. Es de notar la gran variación de la densidad del líquido con la temperatura, desde 1231 kg/m3 en el punto de ebullición normal (Tb=184,5 K) hasta los 452 kg/m3 del punto crítico (Tcr=309,5 K).
b) Entalpía y función de Gibbs de la reacción de descomposición del N2O en sus elementos, en condiciones estándar, interpretando los signos obtenidos. ¿Cómo se calcularía la función de Gibbs de formación estándar del N2O si faltara ese dato en las tablas de datos termoquímicos?
En condiciones estándar el N2O es un gas: Tb=184 K (-89 ºC). Con los Datos termoquímicos:
| > | eq:=N2O=N2+(1/2)*O2;eq9_9b;eq9_9a;eq9_9c;hr_gr_sr(g):=hgs_r25(eq); |
![hrR = Sum(`*`(nu[i], `*`(h[i])), i = 1 .. C)](images/p52_12.gif) |
![grR = Sum(`*`(nu[i], `*`(g[i])), i = 1 .. C)](images/p52_13.gif) |
![srR = Sum(`*`(nu[i], `*`(s[i])), i = 1 .. C)](images/p52_14.gif) |
i.e. la entalpía de reacción estandar (a 25 ºC y 100 kPa el N2O es un gas) es hr=-82 kJ/mol (exotérmica), la gr=-104 kJ/mol (espontánea), y la sr=74 J/(mol·K) es positiva porque aumenta la cantidad de sustancia (1 mol de gas da 1,5 mol de gas). Nótese que son los valores de la reacción de formación del N2O cambiados de signo.
Si no estuviera la g de formación estándar del N2O en la Tabla, como hay redundancia de datos, se podría calcular a partir de la reacción de formación:
| > | eqForm:=N2+(1)*O2=N2O;g[f,N2O]=h[f,N2O]-T25*s[f,N2O];eqsF:=s[f,N2O]=s[std,N2O]-s[std,N2]-(1/2)*s[std,O2];s[std,N2O]=220*J_/(mol_*K_);s[std,N2]=191.5*J_/(mol_*K_);s[std,O2]=205.04*J_/(mol_*K_);eqsF:=s[f,N2O]=(220-191.5-(1/2)*205.04)*J_/(mol_*K_);h[f,N2O]=82.1e3*J_/mol_;g[f,N2O]=subs(dat,rhs(%)-T25*rhs(eqsF)); |
que coincide con la de las Tablas (y, cambiada de signo, es la gr de la descomposición antes calculada).
c) Temperatura adiabática de la descomposición completa del líquido a 6 MPa.
La temperatura inicial será la de equilibrio líquido-vapor, y ahora habrá que tener en cuenta la entalpía de cambio de fase líquido-vapor, o usar los datos del estado líquido del N2O de la Tabla:
| > | Tliq=T[v](p1);Tliq_:=evalf(subs(dat,solve(p1=pv(T),T)));'Yliq_'=TKC(%);N2+(1/2)*O2=N2O(l);hgs:=get_hgs_data("N2O(l)");N2O(l)=N2+(1/2)*O2;PCI_:=hgs[1];eq15_7_2;eqTa:=Ta=T25+PCI/(c[p,N2]+c[p,O2]/2);eqTa_:=subs(PCI=PCI_,cpComp,dat,%) |
![Ta = `+`(T25, `/`(`*`(a, `*`(PCI)), `*`(Sum(`*`(x[Com[i]], `*`(c[p, i])), i = 1 .. CP))))](images/p52_32.gif) |
![Ta = `+`(T25, `/`(`*`(PCI), `*`(`+`(c[p, N2], `*`(`/`(1, 2), `*`(c[p, O2]))))))](images/p52_33.gif) |
i.e. se alcanzarían 1670 K en la descomposición completa del N2O líquido a 25 ºC, luego a 27,5 ºC un poco más (insignificante). El PC entrando líquido es 69,8 kJ/mol en vez de los 82,1 kJ/mol si entrase gaseoso (estado estándar).
d) Composición de equilibrio a esa temperatura y presión, suponiendo que también aparece NO.
| > | eqMix:=eqMIX(a*N2O=[2,3,11,13]);eqNX;eqBO;eqBN;eq0:=eq;eqEQ0_:=evalf(subs(p=p1,T=rhs(eqTa_),dat,eqEQ(eq)));eq1:=(1/2)*N2+(1/2)*O2=NO;eqEQ1_:=evalf(subs(p=p1,T=rhs(eqTa_),dat,eqEQ(eq1)));s:=solve({eqNX,eqBO,eqBN,eqEQ0_,eqEQ1_},{a,x[NO],x[N2O],x[N2],x[O2]});1e6*x[N2O]=subs(s,x[N2O])*1e6;1000*x[NO]=subs(s,x[NO])*1000; |
![`/`(`*`(`^`(x[O2], `/`(1, 2)), `*`(x[N2])), `*`(x[N2O])) = 359660.3583](images/p52_40.gif) |
![`/`(`*`(x[NO]), `*`(`^`(x[O2], `/`(1, 2)), `*`(`^`(x[N2], `/`(1, 2))))) = 0.6551248491e-2](images/p52_42.gif) |
i.e. de NO aún se formaría un 0,3 % molar en el equilibrio, pero el N2O desaparecería por completo (habría 1 ppm).
El N2O es un gas de efecto invernadero con GWP=300, cuya concentración en la atmósfera también está aumentando mucho (por la agricultura intensiva), de las 0,27 ppm_vol en 1750 a las 0,33 ppm_vol en 2018, siengo el más dañino tras el CO2 y el CH4. Además, el daño que causa a la capa de ozono va en aumento (puede que sea el más dañino) pese a su bajo ODP=0,017, porque no entró en las limitaciones del protocolo de Montreal.
| > |