| > | restart:#"m09_p44" |
En una novela (“The Martian”, A. Weir, 2011) se dice que para conseguir 500 L de agua (para regar plantas en una base marciana), se van a usar 250 L de hidracina (N2H4) y otros 250 L de CO2 líquido. La hidracina se obtiene de un depósito de combustible, y se hace gotear sobre el catalizador para descomponerla en N2 y H2. El dióxido de carbono se obtiene de la atmósfera marciana, y se dice que un ‘oxigenador’ da un litro de O2(liq), por cada litro de CO2(liq). Se pide:
a) Calcular la masa, el volumen, y la cantidad de O2(liq) obtenible de 1 L de CO2(liq) por disociación completa. ¿Y si fuesen gases, cuántos litros de O2 se obtendrían de un litro de CO2?
b) En la práctica, la descomposición del CO2 se puede hacer con una primera etapa electrolítica o termolítica que da CO2=CO+½O2, y una segunda etapa catalítica que daría CO=C+½O2. Determinar las entalpías de reacción estándar de las tres reacciones de descomposición del CO2, y compararlas.
c) Determinar la entalpía de reacción estándar de la descomposición de la hidracina, y calcular la temperatura adiabática que alcanzarían los gases.
d) Determinar los volúmenes mínimos de N2H4 y de CO2 líquido para obtener los 500 L de agua.
Datos:
| > | read`../therm_eq.m`:read`../therm_chem.m`:with(therm_chem);with(therm_proc):#Global Elem,Comp,C_,MfComp,cpComp,eqNX,eqBC,eqBH,eqBO,eqBN,eqBS,delta_
|
| > | su1:="H2O":su2:="N2H4":su3:="CO2":su4:="N2":su5:="H2":su6:="O2":dat:=[Vw=0.5*m_^3,Vh=0.25*m_^3,Vc=0.25*m_^3]; |
| (1) |

Eqs. const.:
| > | dat:=op(dat),op(subs(g=g0,[Const])),SI2,SI1:datW:=get_gas_data("H2O"),get_liq_data("H2O"):datF:=M=rhs(Mf(N2H4)),get_liq_data("N2H4"):datC:=get_gas_data("CO2"),get_liq_data("CO2"):datN:=get_gas_data("N2"):datH:=get_gas_data("H2"),get_liq_data("H2"): datO:=get_gas_data("O2"),get_liq_data("O2"): |
a) Calcular la masa, el volumen, y la cantidad de O2(liq) obtenible de 1 L de CO2(liq) por disociación completa. ¿Y si fuesen gases, cuántos litros de O2 se obtendrían de un litro de CO2?
El máximo obtenible en la disociación completa es 1 mol de O2 por cada mol de CO2. Ahora hay que ver las masas molares y densidades. Sea nr1 la relación molar de O2 obtenible por mol de CO2.
| > | eq1:=CO2=C+O2;nr1:=1;nr1_:=nr1*mol_O2/mol_CO2;mr1:=nr1*M_O2/M_CO2;mr1:=subs(M_O2=M,datO,M_CO2=M,datC,%);mr1_:=%*kg_O2/kg_CO2;Vr1:='mr1'*rho_CO2liq/rho_LOX;Vr1:=subs(rho_CO2liq=rho,datC,rho_LOX=rho,datO,%);Vr1_:=%*L_O2liq/L_CO2liq;rho_CO2liq:=subs(datC,rho);plot([[-56.3,1180],[-20,1033],[0,928],[20,770],[30,600]],T_C=-60..30,rho=0..1200); |
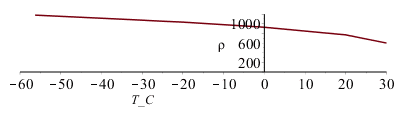 |
i.e. como M=44 g de CO2 dan 32 g de O2, la relación másica es de 32/44=0,73 kg/kg, mientras que la relación volumétrica en fase líquida, tomando rhoCO2=1180 kg/m3, es de 0,75 L/L habiendo tomado la densidad del CO2-líquido en el punto triple, i.e. a -56,3 ºC, aunque a 30 ºC la densidad del CO2liq sería la mitad y por tando solo daría 0,75/2=0,38 L/L de LOX.
En resumen, de 1 L de CO2liq a baja temperatura se obtendrían 0,85 kg de O2, o bien 0,75 L de O2liq_crioggénico, o 27 moles de O2.
Si se tratase de gases en las mismas condiciones de presión y temperatura, efectivamente se obtendría un litro de O2 por cada litro de CO2 con la hipótesis de gases ideales (de pV=nRT, V/n=cte), más un pequeñísimo volumen de partículas de carbono.
Para que el CO2 esté liquido la temperatura ha de estar en el rango Ttr<T<Tcr (i.e. T=-56..31 ºC) y la presión ha de ser mayor que la del punto triple, p>ptr=518 kPa, lo cual es razonable para almacenamiento su en Marte, pero para tener O2liq la temperatura ha de ser <Tcr=155 K=-118 ºC, que parece demasiado fría incluso en Marte (el depósito no podría ser hermético).
NOTA. La temperatura en la superficie de Marte depende mucho de la posición del Sol, con valores típicos sud-ecuatoriales diurnos en el verano marciano de 0..20 ºC, y nocturnos de -80..-50 ºC, que en invierno pasan a ser -30..0 ºC y -100..-70 ºC respectivamente (en las regiones polares puede llegarse a unos -140 ºC en invierno).
b) La descomposición del CO2 más realista consiste en una primera etapa que de descomposición electrolítica o termolítica que da CO2=CO+½O2, y una segunda etapa catalítica CO=C+½O2. Determinar la entalpías de reacción estándar de las tres reacciones de descomposición del CO2.
| > | eq1:=eq1;hgs_1:=hgs_r25(eq1);eq2:=CO2=CO+(1/2)*O2;hgs_2:=hgs_r25(eq2);eq3:=CO=C+(1/2)*O2;hgs_3:=hgs_r25(eq3); |
| (2) |
i.e. la eq1 tiene hrstd=394 kJ/mol, la eq2 283 kJ/mol, y la eq3 111 kJ/mol, todas positivas porque son endotérmicas. Las tres grstd son positivas porque ninguna es espontánea (todas necesitan aport exergético). Nótese que como la eq1 es combinación de la eq2+eq3, también es hr1=hr2+hr3 (ley de Hess).
NOTA. En 2014 se consiguió realizar la reacción eq2 con gran rendimiento a temperaturas ordinarias por electrólisis con electrolito de óxido metálico (antes se hacía por termólisis a alta temperatura).
c) Determinar la entalpía de reacción estándar de la descomposición de la hidracina, y calcular la temperatura adiabática que alcanzarían los gases.
La hideacina solo puede estar líquida en el rango Ttr<T<Tcr (i.e. T=2..380 ºC) y presiones superior a la del punto triple, p>ptr=500 Pa.
Suponiendo descomposición completa:
| > | eq4:=N2H4=N2+2*H2;hgs_4:=hgs_r25(eq4);Tad:=T25+PCI/(c[p,N2]+2*c[p,H2]);PCI_:=PCI(eq4);eqM_:=eqMIX(a*N2H4=[3,8]);sol_:=solve({eqBN,eqBH,eqNX},{a,x[N2],x[H2]});eq15_7_2;cps:=[cpComp[3],cpComp[8]];subs(PCI=PCI_,sol_,cpComp,dat,eq15_7_3);cps:=[c[p,N2]=subs(datN,c[p]*M),c[p,H2]=subs(datH,c[p]*M)];subs(PCI=PCI_,sol_,cps,dat,eq15_7_3); |
![Ta = `+`(T25, `/`(`*`(a, `*`(PCI)), `*`(Sum(`*`(x[Com[i]], `*`(c[p, i])), i = 1 .. CP))))](images/p44_27.gif) |
|
| (3) |
i.e. la entalpía de reacción estándar es de -51 kJ/mol (el signo '-' indica que es exotérmica); el signo '-' de la función de Gibbs de reacción estándar, gr25=-149 kJ/mol, indica que es espontánea. En la reacción completa queda un 33% de N2 y un 67% de H2, que con unos valores medios en caliente de los cp de 34 J/(mol·K), se calentarían hasta 790 K, pero como esta temperatura no es muy alta, aplicamos los valores de cp en frío, resultando una temperatura adiabática de unos 890 K.
NOTA. En la práctica, la presión de funcionamiento en la cámara de reacción suele ser 0.5..2 MPa. El catalizador es una matriz porosa (e.g. de alúmina) impregnada con algún metal noble (e.g. iridio), o con un oxi-carburos de metales de transición como el wolframio. Pero la descomposición de la hidracina no es según N2H4=N2+2H2, sino que se forma bastante amoniaco. Tanto la hidracina como el amoniaco son muy tóxicos.
d) Determinar los volúmenes mínimos de N2H4 y de CO2 líquido para obtener 500 L de agua.
Vemos que el máximo H2 obtenible es de 2 mol de H2 por cada mol de N2H4, y, con las masas molares y densidades:
| > | eq4;nr4:=2;nr4_:=nr4*mol_H2/mol_N2H4;mr4:=nr4*M_H2/M_N2H4;mr4:=subs(M_H2=M,datH,M_N2H4=M,datF,%);mr4_:=%*kg_H2/kg_N2H4;Vr4:='mr4'*rho_N2H4/rho_LH2;Vr4:=subs(rho_N2H4=rho,datF,rho_LH2=rho,datH,%);Vr4_:=%*L_H2liq/L_N2H4liq;rho_H2liq:=subs(datH,rho);rho_N2H4liq:=subs(datF,rho); |
| (4) |
Así que, para obtener 500 L de agua líquida, que a temperaturas ordinarias son unos 500 kg o 500/0,018=27 600 mol de agua, se necesitan 27 600 mol de H2 y 12 800 mol de O2, que con las relaciones de descomposición anteriores requieren un mínimo de 13 800 mol de CO2 y otros 13 800 mol de N2H4, y con las densidades de líquido:
| > | mw:=subs(datW,dat,Vw*rho);nH20:=Vw*rho/M;nH2O_:=subs(datW,dat,%);eq5:=H2O=H2+(1/2)*O2;nH2_:=nH2O_;nO2_:=nH2O_/2;nN2H4:='nH2/2';nN2H4_:=nH2_/2;Vliq_N2H4:='nN2H4'*M/rho;Vliq_N2H4_:=subs(nH2=nH2_,nN2H2=nN2H2_,datF,%);nCO2=nO2;nCO2_:=nO2_;Vliq_CO2:='nCO2'*M/rho;Vliq_CO2_:=subs(nCO2=nCO2_,datC,%); |
| (5) |
Conclusión: no bastan 250 L de CO2liq y 250 L de N2H4liq como se dice en el enunciado, si no que hacen falta al menos 520 L de CO2liq y 440 L de N2H4liq. Y si se supone que el CO2liq está a unos 20 ºC, rho=777 kg/m3 y por tanto harían falta 790 L de CO2liq en vez de los 520 L anteriores.
En principio, podría parecer intuitivo que si para obtener un mol de H2O hace falta 1/2 mol de CO2 y 1/2 mol de N2H4, y las tres substancias en estado líquido tienen casi la misma densidad (1000, 1180, ,1010)... Pero intervienen las masas molares, pues el volumen es V=n*M/rho, y las Ms difieren mucho, siendo 18, 44, y 32 g/mol respectivamente.
| > |