>	restart:#"m09_p00"

Se alimenta con vapor y aire un lecho de carbón (supóngase grafito) a presión y temperatura constantes. Supóngase que los datos son Raire/vapor=1, T1=1000 K y p1= 100 kPa. Se pide:

a) Indicar los productos esperados y determinar la varianza del sistema.

b) Calcular la composición de equilibrio.

c) Calcular la composición de equilibrio y el calor intercambiado en función de la temperatura de salida entre 400 K y 2000 K.

Datos:

>	read`../therm_chem.m`:with(therm_chem):with(therm_proc):

>	su1:="Aire":su2:="H2O":dat:=[T1=1000*K_,p1=1e5*Pa_,b_c=1];

Eqs. const.:

>	Adat:=get_gas_data(su1):Wdat:=get_gas_data(su2),get_liq_data(su2):get_pv_data(su2):dat:=op(dat),op(subs(g=g0,[Const])),Adat,SI2,SI1:

a) Indicar los productos esperados y determinar la varianza del sistema..

Las combinaciones más plausibles de {C,H,O,N} son {CO2,CO,H2O,H2,CH4,CH4O,OH,H,O,NH3,NO,NO2,N2O}.

La varianza, V=2+C-F-R=2+E-F=2+E-2=4 es independiente del número de compuestos.

Podemos elegir como datos la temperatura, la presión, la relación vapor/aire y la proporción de oxígeno en el aire, y con ello queda fijado el estado de equilibrio.

>	V:=2+C-F-R;V:=2+E-F;V_:=2+4-2;

b) Calcular la composición de equilibrio.

Relación de mezcla (mi son los que se supone que salen).

>	eqDat:=subs(dat,b/c=b_c);eqMIX(subs(dat,a*C+b*H2O+c*(c21*O2+c79*N2))=[2,3,4,6,7,8,9,10,11,12,13,14,19,20]);

Incógnitas: a,b,c y xi (3+i)

Ecuaciones: eqDAT,eqNX,eqBC,eqBH,eqBO,eqBN (6) y i+carbono-E=i+1-4 ecuaciones de equilibrio químico (en total hay 3+i incógnitas y 6+i+1-4=3+i ecuaciones).

Ya el valor de la K(T1) de la reacción de formación muestra si va a ser importante algún compuesto.

Estequiometrías

>	eq1:=C+O2=CO2;eqEQ1:=eqEQ(eq1);eqEQ1_:=evalf(subs(T=T1,p=p0,dat,eqEQ1)):evalf(%,2);eq2:=C+(1/2)*O2=CO;eqEQ2:=eqEQ(eq2);eqEQ2_:=evalf(subs(T=T1,p=p0,dat,eqEQ2)):evalf(%,2);eq3:=C+CO2=2*CO;eqEQ3:=eqEQ(eq3);eqEQ3_:=evalf(subs(T=T1,p=p0,dat,eqEQ3)):evalf(%,2);

que enseña que habrá poquísimo O2 (no combiene usarlo), y más CO que CO2 (e.g. si CO2=0,1, CO=sqrt(0.15)=0,4). También enseña que sólo 2 son independientes, pues:

>	eqCheck:=lhs(eqEQ2_)^2/lhs(eqEQ1_)=rhs(eqEQ2_)^2/rhs(eqEQ1_):'eqCheck'=evalf(%,2);

>	eqEQ4:=eqEQ(H2+(1/2)*O2=H2O);eqEQ4_:=evalf(subs(T=T1,p=p0,dat,eqEQ4)):evalf(%,2);eqEQ5:=eqEQ(H2O+CO=H2+CO2);eqEQ5_:=evalf(subs(T=T1,p=p0,dat,eqEQ5)):evalf(%,2);eqEQ6:=eqEQ(C+2*H2=CH4);eqEQ6_:=evalf(subs(T=T1,p=p0,dat,eqEQ6)):evalf(%,2);

que enseña que habrá mucha más H2O que O2, pero menos que H2. De CH4 habrá menos que de H2.

>

eqEQ7:=eqEQ(CO+2*H2=CH4O):eqEQ7_:=evalf(subs(T=T1,p=p0,dat,%));eqEQ8:=eqEQ(H2+O2=2*OH):eqEQ8_:=evalf(subs(T=T1,p=p0,dat,%));eqEQ9:=eqEQ(H2=2*H):eqEQ9_:=evalf(subs(T=T1,p=p0,dat,%));eqEQ10:=eqEQ(O2=2*O):eqEQ10_:=evalf(subs(T=T1,p=p0,dat,%));eqEQ11:=eqEQ(N2+3*H2=2*NH3):eqEQ11_:=evalf(subs(T=T1,p=p0,dat,%));eqEQ12:=eqEQ(N2+O2=2*NO):eqEQ12_:=evalf(subs(T=T1,p=p0,dat,%));

que enseña que de los demás habrá poquísimo.

Primera iteración: combustión teórica.

>	sol1:=solve(subs(x[Comp[2]]=0,seq(x[Comp[i]]=0,i=7..nops(Comp)),dat,{eqNX,eqBC,eqBH,eqBO,eqBN,eqDat}),{a,b,c,x[Comp[3]],x[Comp[4]],x[Comp[5]]}):'sol1'=evalf(%,2);

pero para ver si es buena aproximación se evalúan los demás con esos valores.

>	sol11:=solve(subs(sol1,{eqEQ1_,eqEQ2_})):evalf(%,2);sol12:=solve(subs(sol1,sol11,{eqEQ5_,eqEQ6_})):evalf(%,2);

Primera conclusión: si se llega a formar CH4 o H2 o CO (dependerá de las energías de activación de los catalizadores) su proporción no será traza sino de primer orden en esas condiciones T,p,b_c.

>	sol2:=solve(subs(x[Comp[2]]=0,x[Comp[9]]=0,seq(x[Comp[i]]=0,i=11..nops(Comp)),dat,{eqNX,eqBC,eqBH,eqBO,eqBN,eqDat,eqEQ3_,eqEQ5_,eqEQ6_}),{a,b,c,x[Comp[3]],x[Comp[4]],x[Comp[6]],x[Comp[7]],x[Comp[8]],x[Comp[10]]})[1];

y el H2O era despreciable, así como los demás.

>	sol22:=seq([evalf(eqEQ||i||_,1),evalf(solve(subs(sol2,eqEQ||i||_)),3)],i=1..8);

El calor que sale, por mol de combustible procesado, será:

>	q:=(1/a)*(Sum('x[Comp[i]]*h||i','i'=1..C)+Sum('x[Comp[i]]*c[p||i]*(Ts-T25)','i'=2..C))-c[p,C]*(Te-T25)-(b/a)*c[pa]*(Te-T25)-(c/a)*(h[lv0]+c[pv]*(Te-T25));

>

i:='i':q_:=subs(c[pa]=c[p,N2],c[pv]=c[p,H2O],cpComp,Te=T0,Ts=T1,dat,sol2,x[Comp[2]]=0,x[Comp[9]]=0,seq(x[Comp[i]]=0,i=11..nops(Comp)),h[lv0]=h[lv0]*M,Wdat,dat,(1/a)*(sum(x[Comp[i]]*'h||i||_',i=2..nops(Comp))+sum(x[Comp[i]]*c[p,Comp[i]]*(Ts-T25),i=2..nops(Comp)))-c[p,C]*(Te-T25)-(b/a)*c[pa]*(Te-T25)-(c/a)*(h[lv0]+c[pv]*(Te-T25))):'q'=evalf(%,3);

i.e. exotérmica.

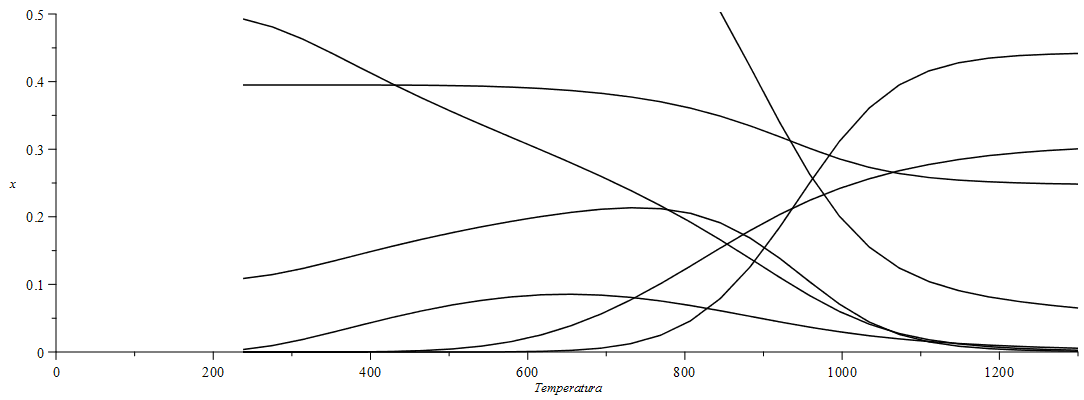
c) Calcular la composición de equilibrio y el calor intercambiado en función de la temperatura de salida entre 400 K y 2000 K.

>

n:=29:arr:=array(1..n,1..8):for i from 1 to n do T:=evalf( 200+1100*(i/n))*K_;sol2:=solve(subs(p=p1,x[Comp[2]]=0,x[Comp[9]]=0,seq(x[Comp[i]]=0,i=11..nops(Comp)),dat,{eqNX,eqBC,eqBH,eqBO,eqBN,eqDat,eqEQ3,eqEQ5,eqEQ6}),{a,b,c,x[Comp[3]],x[Comp[4]],x[Comp[6]],x[Comp[7]],x[Comp[8]],x[Comp[10]]})[1];q_:=subs(c[pa]=c[p,N2],c[pv]=c[p,H2O],cpComp,Te=T0,Ts=T,dat,sol2,x[Comp[2]]=0,x[Comp[9]]=0,seq(x[Comp[ii]]=0,ii=11..nops(Comp)),h[lv0]=h[lv0]*M,Wdat,dat,(1/a)*(sum(x[Comp[ii]]*'h||ii||_',ii=2..nops(Comp))+sum(x[Comp[ii]]*c[p,Comp[ii]]*(Ts-T25),ii=2..nops(Comp)))-c[p,C]*(Te-T25)-(b/a)*c[pa]*(Te-T25)-(c/a)*(h[lv0]+c[pv]*(Te-T25)));arr[i,1]:=T/K_;arr[i,2]:=subs(SI0,-q_)/1e6;arr[i,3]:=subs(sol2,x[Comp[3]]);arr[i,4]:=subs(sol2,x[Comp[4]]);arr[i,5]:=subs(sol2,x[Comp[6]]);arr[i,6]:=subs(sol2,x[Comp[7]]);arr[i,7]:=subs(sol2,x[Comp[8]]);arr[i,8]:=subs(sol2,x[Comp[10]]);od:  pl2:=pla(arr,2,1):pl3:=pla(arr,3,1):pl4:=pla(arr,4,1):pl5:=pla(arr,5,1):pl6:=pla(arr,6,1):pl7:=pla(arr,7,1):pl8:=pla(arr,8,1):plot([pl2,pl3,pl4,pl5,pl6,pl7,pl8],Temperatura=0..1300,x=0..0.5,color=black);

>