| > | restart:#"m08_p73" |
ConsidÃĐrese el siguiente sistema de secado. Se toma aire ambiente a 25 šC y 40% de HR con una soplante que consume 200 W, y se calienta con una resistencia elÃĐctrica hasta 55 šC; este aire calienta pasa sobre el material hÚmedo en un tÚnel de secado de 0,6 m de ancho y 0,3 m de alto, de donde sale a 30 šC. Se quiere extraer 5 kg/h de agua. Se pide:
a) Esquema de la instalaciÃģn, del proceso que sufre el aire (diagrama h-w), y humedad relativa a la salida.
b) Gasto de aire necesario, velocidad media a la entrada de la cÃĄmara de secado, y potencia necesaria del calentador.
c) Se quiere estudiar el cambio del circuito abierto anterior por un circuito cerrado de aire en el que se mantendrÃan las condiciones termohigromÃĐtricas en la cÃĄmara de secado (de entrada y salida). Para ello, el aire a la salida de la cÃĄmara se pasarÃa por el vaporizador de una bomba de calor que lo enfriarÃa y condensarÃa hasta el punto de rocÃo del aire ambiente, pasando luego por el calentador, que en lugar de la resistencia elÃĐctrica es parte del condensador de la bomba de calor. Hacer un esquema de la nueva instalaciÃģn, y del proceso que sufre el aire.
d) Determinar el punto de rocÃo del aire ambiente, y el calor a evacuar en el vaporizador.
e) Potencia necesaria del compresor de la bomba, suponiendo que su eficiencia exergÃĐtica es un 60% de la correspondiente a la de Carnot a las temperaturas de cambio de fase en los cambiadores, en los que habrÃĄ que dejar un salto mÃnimo de 5 šC entre corrientes.
Datos:
| > | read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):with(plots): |
| > | su1:="Aire":su2:="H2O":dat:=[T0=(25+273.15)*K_,phi0=0.40,Wfan=200*W_,T1=(55+273.15)*K_,Lx=0.6*m_,Ly=0.3*m_,T2=(30+273.15)*K_,mw=(5/3600)*kg_/s_,DT=5*K_,eta[x]=0.60]; |
Eqs. const.:
| > | Adat:=get_gas_data(su1):Adat:=subs(c[p]=c[pa],R=R[a],M=M[a],T[b]=nada,[Adat]):Wgdat:=get_gas_data(su2):Wgdat:=subs(c[p]=c[pv],R=R[v],M=M[v],[Wgdat]):Wldat:=get_liq_data(su2):Wdat:=op(Wgdat),Wldat:get_pv_data(su2):dat:=op(dat),Const,SI2,SI1: |
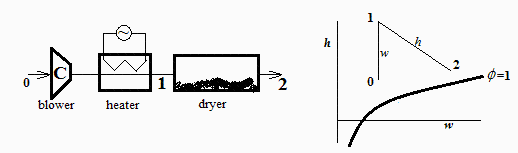
a) Esquema de la instalaciÃģn, del proceso que sufre el aire (diagrama h-w), y humedad relativa a la salida.
Supondremos que en la soplante (que es un compresor de muy baja relaciÃģn de presiones, C) apenas se calienta el aire (gran parte del consumo se disiparÃĄ en el motor elÃĐctrico de la soplante, y, de lo que vaya al flujo de aire, parte contribuirÃĄ al incremento de presiÃģn y velocidad, y otra parte se disiparÃĄ por fricciÃģn). Luego se puede ver que despreciar una adiciÃģn del orden 100 W no es importante. Consideraremos, por tanto, que todo el proceso que sufre el aire (aspiraciÃģn, calentamiento, y humidificaciÃģn) es a presiÃģn constante de 100 kPa. NÃģtese que, en el tÚnel, el aire toma agua del material a secar, i.e. el material se seca y el aire se humedece.
De 0 a 1 se conserva la humedad absoluta (w0=w1), y de 1 a 2 es adiabÃĄtico (serÃa absurdo dejar que se escapara mucho calor por las paredes del secadero). En principio podrÃamos suponer que a la salida el aire estÃĄ saturado (lÃmite termodinÃĄmico), pero como nos dan el punto 1 (T1,w1) y sabemos la T2 y que de 1 a 2 es adiabÃĄtico, el punto 4 estarÃĄ donde se corten T2 y h1 en el diagrama h-w.
| > | eq8_8;w0_:=evalf(subs(dat,w(phi0,T0,p0)));eq8_11;h0_:=subs(Adat,Wdat,T=T0,dat,h(T,w0_));w1_:=w0_;h1_:=subs(Adat,Wdat,T=T1,dat,h(T,w0_));eqBE12:=ma*(h2-h1)=0;h2_:=h1_;w2_:=subs(Adat,Wdat,T=T2,h=h2_,dat,solve(eq8_11,w));phi2_:=evalf(subs(dat,phi(w2_,T2,p0))); |
))), `-`(1))))](images/np731_3.gif) |
|
| (1) |
i.e. el aire sale del secadero con un 66% de HR, no saturado (con esto se consigue que el tÚnel de secado sea mÃĄs corto, a expensas de gastar mÃĄs aire).
b) Gasto de aire necesario, velocidad media a la entrada de la cÃĄmara de secado, y potencia necesaria del calentador.
El aire necesario para que pasando de w1=8 g/kg a w2=18 g/kg en el secadera extraiga 5 kg/h de agua es:
| > | eqBMw:=mw=ma*(w2-w1);ma_:=subs(dat,mw/(w2_-w1_));eqm:=m=rho*v*A;eqET:=rho=p/(R*T);eqET_:=subs(p=p0,T=T1,R=R[a],Adat,dat,%);A_:=subs(dat,Lx*Ly);v_:=subs(eqET_,dat,ma_/(rho*A_));eqBE01:=W=ma*(h1-h2);W_:=subs(dat,ma_*(h1_-h0_));eqeta:=eta[Dryer]=mw/(Wfan+Wheat);subs(Wheat=W_,dat,%);lhs(eqeta)=subs(SI0,rhs(%))*3.6e6*kg_/kWh_; |
| (2) |
i.e. hay que mover 0,14 kg/s (unos 10 m3/min) de aire a 0,7 m/s, consumiendo 4.2 kW en calentarlo (y los 200 W en impulsarlo). NÃģtese que la soplante consume mucha menos energÃa que el calentador.
Puede compararse este consumo unitario de 4,4 kW por cada 1,4 g/s de agua evaporada, i.e. 4,4/1,4=3,1 MJ/kg, con el de pasar agua de 25 šC a vapor a 100 šC, que es 4,2·(100-25)+2260=2,6 MJ/kg, y comprobar que no solo se ha evaporado el agua sino que se ha calentado el aire.
Una figura de mÃĐrito usada en sistemas de secado es mw/W en kg de agua evaporada por kWh consumido:5/(0,2+4,2)=1,1 kg/kWh.
c) Se quiere estudiar el cambio del circuito abierto anterior por un circuito cerrado de aire en el que se mantendrÃan las condiciones termohigromÃĐtricas en la cÃĄmara de secado (de entrada y salida). Para ello, el aire a la salida de la cÃĄmara se pasarÃa por el vaporizador de una bomba de calor que lo enfriarÃa y condensarÃa hasta el punto de rocÃo del aire ambiente, pasando luego por el calentador, que en lugar de la resistencia elÃĐctrica es parte del condensador de la bomba de calor. Hacer un esquema de la nueva instalaciÃģn, y del proceso que sufre el aire.
Ahora el aire entrarÃa
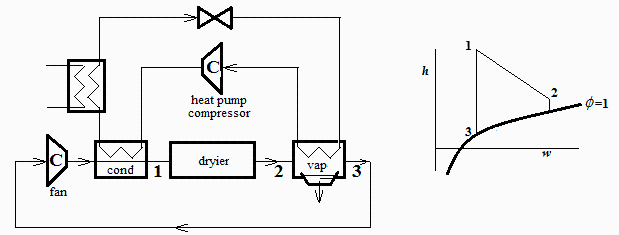
d) Determinar el punto de rocÃo del aire ambiente, y el calor a evacuar en el vaporizador.
| > | eq8_9;TR0_:=evalf(subs(dat,solve(pv(TR)=phi0*pv(T0),TR)));'TR0_'=TKC(%);hR0_:=subs(Adat,Wdat,T=TR0_,dat,h(T,w0_));eqBEvap:=Qvap=ma*(h2-hR0);Qvap_:=subs(dat,ma_*(h2_-hR0_)); |
| (3) |
i.e. hay que enfriar el aire hasta 10,4 šC (condensarÃĄ toda el agua evaporada en el secadero, pues el gasto de aire y las humedades absolutas no varÃan), para lo que hay que extraer 6,3 kW.
e) Potencia necesaria del compresor de la bomba, suponiendo que su eficiencia exergÃĐtica es un 60% de la correspondiente a la de Carnot a las temperaturas de cambio de fase en los cambiadores, en los que habrÃĄ que dejar un salto mÃnimo de 5 šC entre corrientes.
Para enfriar el aire hasta 10,4 šC con 5 šC de salto mÃnimo, el vaporizador ha de estar a 5,4 šC (o mÃĄs frÃo), y para calentar luego el aire hasta 55 šC, el condensador ha de estar a 60 šC (o mÃĄs).
Como aquà lo que interesa es el efecto refrigerante de la bomba de calor, el rendimiento de Carnot serÃa Tvap/(Tcond-Tvap).
| > | Tvap:=TR0-DT;Tvap_:=subs(dat,TR0_-DT);'Tvap_'=TKC(%);Tcond:=T1+DT;Tcond_:=subs(dat,T1+DT);'Tcond_'=TKC(%);etaRefrCarnot:=eta[RC]='Tvap/(Tcond-Tvap)';etaRefrCarnot:=eta[RC]=Tvap_/(Tcond_-Tvap_);WCarnot:=Qvap/eta[RC];WCarnot_:=subs(etaRefrCarnot,Qvap_/eta[RC]);Wcompr:='WCarnot/eta[x]';Wcompr_:=subs(dat,WCarnot_/eta[x]); |
| (4) |
i.e. con la bomba solo se consumen 2.1 kW (aparte de los 0,2 kW de la soplante) para el secado del material, mientras que con la resistencia elÃĐctrica era 4,2 kW (mÃĄs los 0,2 kW). La eficacia ha pasado de 5/(4,2+0,2)=1,1 kg de agua por kWh, al doble, 5/(2.1+0,2)=2,2 kg/kWh.
NÃģtese que sobra calor en el condensador, que evacua 8,4 kW y el aire solo necesita 6,3 kW para pasar de 10,4 šC a 55 šC.
| > | eqBE_BC:='Qcod=Qvap+Wcompr';eqBE_BC_:=Qcond=Qvap_+Wcompr_:%;Qheat:=ma*(h1-hR0);Qheat_:=subs(dat,ma_*(h1_-hR0_)); |
| (5) |
| > |