p531.html

> restart:#"m18_p53"

El equipo de aire acondicionado de un coche, toma 2 kW de potencia del motor. Suponiendo que se quiera enfriar hasta 10 ºC el aire en el evaporador, que el aire del condensador puede estar a 50 ºC, que hay que dejar 10 ºC de salto mínimo en los intercambiadores, y que el rendimiento isentrópico del compresor de R134a es del 70 %, se pide (resolver con el modelo de sustancia perfectas, y comparar con los datos del gráfico del R134a):
a) Esquema de los procesos que sufre el refrigerante, en los diagramas T-s y p-h, indicando presiones y temperaturas de trabajo.
b) Temperatura máxima del fluido de trabajo.
c) Gasto de refrigerante, y fracción másica vaporizada en la válvula.
d) Capacidad de refrigeración.
e) Rendimiento energético (COP).

Datos:

> read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):with(therm_proc):with(ThermophysicalData):with(CoolProp):with(Units[Standard]):with(plots):

> su1:="CF3CH2F":dat:=[Wdot=2e3*W_,T1a=(10+273.15)*K_,T3a=(50+273.15)*K_,eta[C]=0.7,DT=10*K_];

> dat:=op(dat),get_gas_data(su1),get_liq_data(su1),Const,SI2,SI1:get_pv_data(su1):

a) Esquema de los procesos que sufre el refrigerante, en los diagramas T-s y p-h, indicando presiones y temperaturas de trabajo.
b) Temperatura máxima del fluido de trabajo..

> T1:=T1a-DT;T1_:=subs(dat,%);'T1_'=TKC(%);p1=p[v](T1);p1_:=subs(dat,evalf(subs(dat,pv(T1))));T3:=T3a+DT;T3_:=subs(dat,%);'T3_'=TKC(%);p2=p[v](T3);p2_:=subs(dat,evalf(subs(dat,pv(T3))));

(1)

i.e. las temperaturas de cambio de fase serán T1=273 K y T3=333 K, y las presiones de trabajo serán (por Antoine) 0,3 MPa y 1,7 MPa. Mirando en el Gráfico p-h del R134a se observan valores similares: p1=2,9 bar y p2=16 bar, este último obtenido por interpolación logarítmica (la isoterma bifásica de 60 ºC queda al 80 % desde 10 MPa a 20 MPa, que corresponde a 10^0,8=6,3, luego 10+6=16).

b) Temperatura máxima del fluido de trabajo.

> ;T2:=T1*(1+((p2/p1)^((gamma-1)/gamma)-1)/eta[C]);'gamma'=subs(dat,gamma);T2_:=subs(p1=p1_,p2=p2_,dat,T2);'T2_'=TKC(%);;

`*`(`+`(T1a, `-`(DT)), `*`(`+`(1, `/`(`*`(`+`(`^`(`/`(`*`(p2), `*`(p1)), `/`(`*`(`+`(gamma, `-`(1))), `*`(gamma))), `-`(1))), `*`(eta[C])))))

(2)

La temperatura máxima del ciclo es de 345 K (72 ºC). Con el Gráfico p-h se encuentra T2s=68 ºC como intersección de s1 y p2, que corresponde a h2s=435 kJ/kg. Por otra parte, h1=398 kJ/kg. Del rendimiento del compresor se deduce h2=h1+(h2s-h1)etaC=398+(435-398)/0,7=451 kJ/kg, que a p2=16 bar corresponde a 80 ºC.

c) Gasto de refrigerante, y fracción másica vaporizada en la válvula.

Con el modelo de sustancia perfecta y entalpía de referencia nula para el líquido en el punto triple (Ttr=Tf=177 K):

> eqC:=Wdot=mdot*c[p]*('T2'-'T1');c[p]=subs(dat,c[p]);mdot_:=subs(dat,Wdot/(c[p]*(T2_-T1)));eqh34:=h3=(1-x4)*h4L+x4*h4V;h3_:=subs(dat,T=T3_,dat,hl(T));h4L_:=subs(dat,T=T1_,dat,hl(T));h4V_:=subs(dat,T=T1_,dat,hv(T));x4=(h3-h4L)/(h4V-h4L);x4_:=(h3_-h4L_)/(h4V_-h4L_);

(3)

i.e. ha de circular un gasto de R134a de 0,033 kg/s, y en la válvula se vaporiza el 38 % másico. Del Grafico se deduce (bajando verticalmente desde el punto 3 a la p1) x4=43 % El gasto de refrigerante será mR=Wcomp/(h2-h1)=2/(451-398)=0,038 kg/s..

d) Capacidad de refrigeración.

> eqR:=QRdot=mdot*(h1-h4);hv=hv(T);hl=hl(T);h4=h3;h1_:=subs(dat,T=T1,dat,hv(T));h3_:=subs(dat,T=T3,dat,hl(T));QRdot_:=subs(dat,mdot_*(h1_-h3_));

(4)

i.e. el aparato extrae 4,1 kW del aire de cabina. Del Grafico se deduce QR=mR*(h1-h4)=0,033·(398-287)=3,7 kW

e) Rendimiento energético (COP).

> eqCOP:=eta=QRdot/Wdot;eqCOP_:=subs(dat,QRdot_/Wdot);

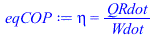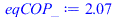(5)

i.e. la eficiencia es 2,1 con el modelo de sustancia perfecta, y 3,7/2=1,9 con los datos del gráfico.

AÑADIDO. Resolución más exacta con el modelo CoolPro de ecuación de estado cúbica que trae el Maple-2016.

> T1_:=(T1_/K_)*Unit('K');'T1_'=convert(%,temperature,degC);p1_:=PropsSI("P","T",T1_,"Q",1,R134a,'useunits');T3_:=(T3_/K_)*Unit('K');'T3_'=convert(%,temperature,degC);p2_:=PropsSI("P","T",T3_,"Q",0,R134a,'useunits');

(6)

i.e. 293 kPa y 1,68 MPa en vez de 295 kPa y 1,69 MPa.

b) Temperatura máxima del fluido de trabajo.

> T2s_:=PropsSI("T",P,p2_,S,PropsSI("S",P,p1_,Q,1,R134a),R134a,'useunits');'T2s_'=convert(%,temperature,degC);h2s_:=PropsSI("H",P,p2_,T,T2s_,R134a);h1_:=PropsSI("H",P,p1_,Q,1,R134a);h2_:=h1_+(h2s_-h1_)/subs(dat,eta[C]);T2_:=PropsSI("T",P,p2_,H,h2_,R134a,'useunits');'T2_'=convert(%,temperature,degC);

(7)

i.e. la Tmax=79 ºC y no los 72 ºC del modelo de sustancia perfecta.

c) Gasto de refrigerante, y fracción másica vaporizada en la válvula.

> h3_:=PropsSI("H",P,p2_,Q,0,R134a);Wdot_:=subs(dat,(Wdot/W_))*Unit('watt');mdot_:=Wdot_/(h2_-h1_);x4_:=PropsSI("Q",P,p1_,H,h3_,R134a);

(8)

i.e. resulta que el gasto es 0,04 kg/s y no 0,03 kg/s, y la salida de la válvula es con 44 % de fracción másica de vapor en vez del 38 % que nos daba antes.

d) Capacidad de refrigeración.
e) Rendimiento energético (COP).

> QRdot_:=mdot_*(h1_-h3_);eq_eta:=QRdot/Wdot=QRdot_/Wdot_

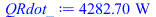(9)

extrae 4,3 kW en vez de 4,1 kW, y el COP es ligeramente mayor (2,14 frente a 2,07).

Y la construcción de diagramas de proceso es muy sencilla:

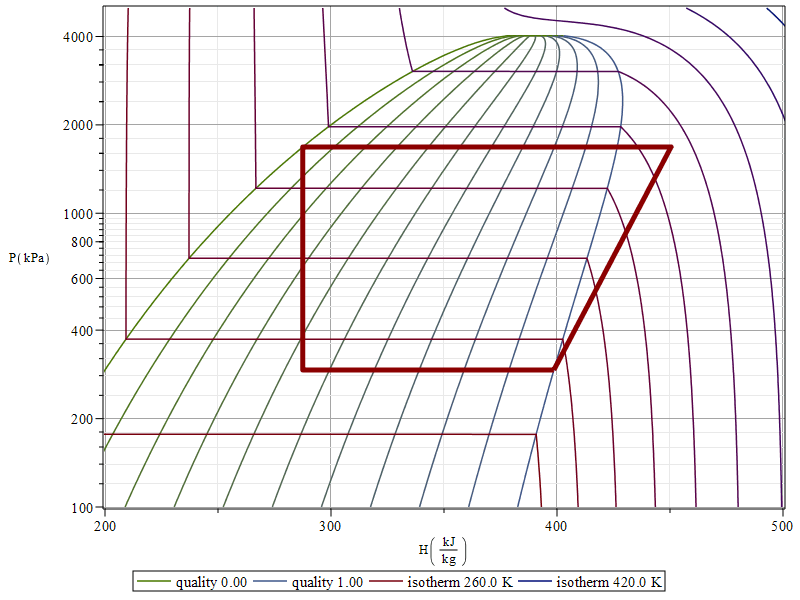
> phChart:=PHTChart(R134a,100*Unit('kPa')..5000*Unit('kPa'),200*Unit('kJ/kg')..500*Unit('kJ/kg')):pts:=convert([[h1, P1], [h2, P2], [h3, P2], [h3, P4], [h1, P1]], unit_free);pts:=`~`[`~`[convert]]([[h1_,p1_],[h2_,p2_],[h3_,p2_],[h3_,p1_],[h1_,p1_]], unit_free);# ~ means element-wise; e.g. sin~(<1,2,3>);

(10)

> Rcycle:=pointplot(`~`[`*`](0.1e-2,pts),connect=true,color="DarkRed",thickness=5):display(phChart,Rcycle)

Plot_2d

Con los datos más exactos del NIST apenas hay diferencia.

> p1_:=293e3*Pa_;h1_:=398.6e3*J_/kg_;s1_:=1727*J_/(kg_*K);p2_:=1.682e6*Pa_;h3_:=287.5e3*J_/kg_;h2s_:=435e3*J_/kg_;h2_:=subs(dat,h1_+(h2s_-h1_)/eta[C]);T2_:=(79.3+273.15)*K_;x4_:=0.44;mdot_:=subs(dat,Wdot/(h2_-h1_));QRdot_:=mdot_*(h1_-h3_);eta=subs(dat,QRdot_/Wdot);

(11)