| > | restart:#"m18_p52" |
Se quiere estimar el coste energético para obtener 1 kg/h de hidrógeno líquido a partir del gas en condiciones ambiente. Se pide:
a) Calcular el calor a evacuar y el coste energético mínimo (límite termodinámico).
b) Coste energético si se usara un ciclo refrigerador de Carnot con un salto mínimo de 5 ºC para transmitir calor con la fuente y el sumidero térmicos.
c) Repetir el caso anterior pero suponiendo que se usan dos máquinas de refrigeración, una para extraer calor a 15 K y soltarlo a 80 K, y otra que toma todo ese calor a 75 K para evacuarlo al ambiente, suponiendo que el rendimiento (COP) de dichas máquinas fuera la mitad del de Carnot.
d) Ciñéndonos a la última de las máquinas (la de alta temperatura), se va a calcular el coste energético para el siguiente caso práctico. Se toma nitrógeno gaseoso en condiciones ambientes; se comprime hasta 32 MPa usando ocho compresores en serie, de rendimiento 0,85, con enfriamiento intermedio al ambiente; se pasa por un recuperador de calor donde se enfría hasta 150 K, y se estrangula (expansión Joule-Thomson) hasta 100 kPa; recoge el calor que desprende la máquina de baja temperatura, y entra como vapor saturado al recuperador de calor antedicho. Hacer un esquema del proceso en un diagrama p-h.
e) Establecer las ecuaciones para resolver el apartado anterior.
Datos:
| > | read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):with(therm_proc):with(ThermophysicalData):with(CoolProp):with(Units[Standard]):with(plots): |
| > | su1:="H2":su2:="N2":dat:=[ml=1/(3600)*kg_/s_,DT=5*K_,Ti=75*K_,Wratio=2,N=8,pB=32e6*Pa_,eta[C]=0.85]; |
| > | dat:=op(dat),get_gas_data(su1),get_liq_data(su1),Const,SI2,SI1:get_pv_data(su1):Hydrogen_cp_Tf_Tb_hlvb:=subs(dat,[c[p],T[f],T[b],h[lv0]]);Ndat:=get_gas_data(su2),get_liq_data(su2):pvN:=get_pv_data(su1):Nitrogen_cp_Tf_Tb_hlvb:=subs(Ndat,[c[p],T[f],T[b],h[lv0]]); |
| (1) |
a) Calcular el calor a evacuar y el coste energético mínimo (límite termodinámico).
| > | Wmin:=m*Dphi;Wmin:=m*(Dh-T0*Ds);Dh:=-h[lv0]+c[p]*(T[b]-T0);Ds:=-h[lv0]/T[b]+c[p]*ln(T[b]/T0);Dh_:=subs(dat,Dh):'Dh'=evalf(%,2);Ds_:=subs(dat,evalf(subs(dat,Ds))):'Ds'=evalf(%,2);ml_:=subs(dat,ml):'ml_'=%*1e3*g_/kg_;QR:=-ml*'Dh';QR:=subs(dat,%);Wmin_:=subs(dat,ml*(Dh_-T0*Ds_)); |
| (2) |
i.e. hay que extraer 1,2 kW del H2 (1,05 kW para enfriar el gas y 0,13 kW para licuarlo), y el coste energético mínimo (inalcanzable) sería de 3,6 kW. Con datos del NIST, Dh=-0-3787=-3787 kJ/kg, Ds=0-53=-53 kJ/(kg·K), luego Dpsi=-3787+288·53=11500 kJ/kg y por tanto Q=1,05 kW y Wmin=0,28·11500=3,2 kW.
b) Coste energético si se usara un ciclo refrigerador de Carnot con un salto mínimo de 5 ºC para transmitir calor con la fuente y el sumidero térmicos.
La máquina de Carnot habría de bombear toda la entalpía DH=ml·Dh, desde 20-5=15 K hasta 15+5=20 ºC.
| > | eqR:=eta[COP]=Q[R]/W;W[Carnot_DT]:=ml*'Dh'/eta[COP];eqRCarnot:=eta[COP]=T2/(T1-T2);T2:=T[b]-DT;T1:=T0+DT;T2_:=subs(dat,T2);T1_:=subs(dat,T1);eqRCarnot_:=subs(dat,eqRCarnot);W[Carnot_DT]:=subs(eqRCarnot_,dat,-ml*Dh/eta[COP]); |
| (3) |
i.e. casi 22 kW en vez de los 3,6 kW del mínimo termodinámico. Incluso sin los 5 ºC de salto térmico ya haría falta casi 16 kW. Como se ve, el ciclo simple de Carnot es muy poco eficiente a tan bajas temperaturas.
a) Repetir el caso anterior pero suponiendo que se usan dos máquinas de refrigeración, una para extraer calor a 15 K y soltarlo a 80 K, y otra que toma todo ese calor a 75 K para evacuarlo al ambiente, suponiendo que el rendimiento COP de dichas máquinas sea la mitad del de Carnot.
Para la máquina de abajo:
| > | T2:='T2':T1:='T1':eqRCarnotLo:=eta[COP]=T2/(T1-T2);T2:=T[b]-DT;T1:=Ti+DT;T2_:=subs(dat,T2);T1_:=subs(dat,T1);eqRCarnotLo_:=subs(dat,eqRCarnotLo);QR1:=-'ml'*'Dh';QR1_:=subs(dat,-ml*Dh);W[CarnotLo]:=subs(eqRCarnotLo_,dat,-ml*Dh/eta[COP]);W[Lo]:=Wratio*W[CarnotLo]:W[Lo]:=subs(dat,%);QLoUp:=QR1_+W[Lo]; |
| (4) |
i.e. la de abajo, con un rendimiento real de 0,23/2=12 % (mitad del de Carnot), consume 10 kW de trabajo, y los echa (junto a los 1,2 kW que extrae del H2), a la de arriba, para la cual:
| > | T2:='T2':T1:='T1':eqRCarnotUp:=eta[COP]=T2/(T1-T2);T2:=Ti;T1:=T0+DT;T2_:=subs(dat,T2);T1_:=subs(dat,T1);eqRCarnotUp_:=evalf(subs(dat,eqRCarnotUp));W[CarnotUp]:='QLoUp'/eta[COP];W[CarnotUp]:=subs(eqRCarnotUp_,dat,%);W[Up]:=subs(dat,Wratio*%);W[tot]:=W[Lo]+W[Up]; |
| (5) |
la de arriba, con un rendimiento real de 0,34/2=17 %, consumiría 66 kW, por lo que el consumo total es de 76 kW.
Nótese que sería mucho mejor usar las dos máquinas secuencialmente en vez de en cascada, i.e. con la máquina de alta enfriar el gas hasta 80 K, y con la de baja completar el enfriamiento del gas y el cambio de fase.
| > | Qup:=m*c[p]*(T0-T80);Qlo:=m*(c[p]*(T80-T[b]-DT)+h[lv0]);T80_:=80*K_;Qup_:=subs(m=ml,T80=T80_,dat,Qup);Qlo_:=subs(m=ml,T80=T80_,dat,Qlo);eqRCarnotUp:=eta[COP]=(T80-DT)/(T0-T80+2*DT);Ti:=T80-DT;Ti_:=subs(dat,T80_-DT);eqRCarnotUp_:=evalf(subs(T80=T80_,dat,eqRCarnotUp));W[CarnotUp]:=Qup/eta[COP];W[CarnotUp]:=subs(m=ml,T80=T80_,eqRCarnotUp_,dat,%);W[up]:=Wratio*W[CarnotUp]:W[up]:=subs(dat,%);eqRCarnotLo:=eta[COP]=(T[b]-DT)/(T0-T[b]+2*DT);eqRCarnotLo_:=evalf(subs(dat,eqRCarnotLo));W[CarnotLo]:=Qlo/eta[COP];W[CarnotLo]:=subs(eqRCarnotLo_,m=ml,T80=T80_,dat,%);W[lo]:=Wratio*W[CarnotLo]:W[lo]:=subs(dat,%);W[tot]:=W[lo]+W[up] |
![`/`(`*`(m, `*`(c[p], `*`(`+`(T0, `-`(T80))))), `*`(eta[COP]))](images/p521_53.gif) |
|
![`/`(`*`(m, `*`(`+`(`*`(c[p], `*`(`+`(T80, `-`(T[b]), `-`(DT)))), h[lv0]))), `*`(eta[COP]))](images/p521_58.gif) |
|
| (6) |
i.e. ahora la de arriba solo consumiría 4,8 kW (y no 66 kW), y la de abajo 13 kW (en vez de 10 kW), por lo que el consumo total sería de 17 kW en vez de 76 kW).
d) Ciñéndonos a la última de las máquinas (la de alta temperatura), se va a calcular el coste energético para el siguiente caso práctico. Se toma nitrógeno gaseoso en condiciones ambientes; se comprime hasta 32 MPa usando ocho compresores en serie, de rendimiento 0,85, con enfriamiento intermedio al ambiente; se pasa por un recuperador de calor donde se enfría hasta 150 K, y se estrangula (expansión Joule-Thomson) hasta 100 kPa, entrando después en un evaporador donde recoge el calor que desprende la máquina de baja temperatura, y del cual sale como vapor saturado al recuperador de calor antedicho. Hacer un esquema del proceso en un diagrama p-h.
Tomando como salución óptima para las relaciones de presión pi=(pB/pA)^(1/N)=32^(1/8)=2,06, lo cual sería exacto en el caso de un gas perfecto (y suficientemente aproximado en nuestro caso), sería:

e) Establecer las ecuaciones para resolver el apartado anterior.
Con ayuda del diagrama p-h (el modelo de sustancia perfecta no vale a tan altas presiones) determinamos hA, hB, y hC (hD=hC), y con el balance energético del ciclo determinamos el gasto circulante de nitrógeno, mN2, y el consumo de los compresores WN2=mN2·wtot.
| > | eqpi_opt:=pi=(pB/pA)^(1/N);eqpi_opt_:=subs(pA=p0,dat,%);w1:=c[p]*T0*(pi^((gamma-1)/gamma)-1);w1_:=subs(Ndat,eqpi_opt_,dat,%);wtot:=N*'w1';wtot_:=subs(dat,N*w1_);hA_:=300e3*J_/kg_;hB_:=260e3*J_/kg_;hC_:=40e3*J_/kg_;hD_:=40e3*J_/kg_;eqBE:=mN2*(hA-hD)=mN2*(hB-hC)+QupN2;WN2:=mN2*'wtot'; |
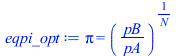 |
|
| (7) |
Si el calor a evacuar por el ciclo de N2 es solo el de enfriar el H2 desde 288 K hasta 80 K (i.e. los 820 W de la solución en serie y no los 11 kW de la solución en cascada):
| > | QupN2_:=Qup_;mN2_:=subs(QupN2=QupN2_,hA=hA_,hB=hB_,hC=hC_,hD=hD_,dat,solve(eqBE,mN2));WN2_:=subs(dat,mN2_*wtot_); |
| (8) |
i.e. usando esta máquina de refrigeración con nitrógeno (un ciclo Linde simple), el consumo energético sería de 11 kW en vez de los 4,8 kW antes estimados con el modelo de Carnot.
Con este ciclo de N2 se enfriaría el H2 hasta 80 K, y luego habría que disponer otra máquina que completase la licuación (e.g. usando He en vez de N2 como fluido de trabajo).
| > |