>	restart:#"m18_p51"

Para enfriar un equipo electrónico instalado en la punta del ala de un avión, sin tener que usar el equipo de aire acondicionado de este, se piensa incorporar allí el equipo siguiente. Se dispone una toma dinámica donde se decelera una corriente de 0,1 kg/s de aire exterior (supondremos proceso ideal de remanso del estado 0 al 1), la cual pasa por una pequeña turbina (proceso de 1 a 2, con rendimiento isoentrópico 0,85), y después por el equipo a enfriar, que debe mantenerse a menos de 50 ºC. Este flujo de aire, tras enfriar el equipo (proceso de 2 a 3), entra en un compresor de rendimiento 0,80 (proceso de 3 a 4) que lo expulsa al exterior con una velocidad pequeña. Suponiendo que se vuela a 270 m/s en aire a 25 kPa y 250 K, que se ha de dejar un salto de 50 K para que la transmisión de calor sea efectiva, y despreciando la pérdida de presión del aire al pasar por el equipo a enfriar, se pide:
a) Cálculo de las condiciones de remanso a la entrada, y esquema en un diagrama T-s de todos los procesos.
b) Temperatura de salida de la turbina, en función de la presión de salida de esta (p2), y potencia generada. Aplicación para p2=15 kPa.
c) Determinar el valor de p2 para que el trabajo que produce la turbina iguale al que consume el compresor.
d) Calcular el calor evacuado del equipo.
Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):with(RealDomain):

>	su1:="Aire":dat:=[p0=25e3*Pa_,T0=250*K_,v0=270*m_/s_,eta[T]=0.85,Teq=(50+273.15)*K_,m=0.1*kg_/s_,eta[C]=0.80,DT=50*K_,p2_15=15e3*Pa_];

>	dat:=op(dat),get_gas_data(su1),Const,SI2,SI1:

a) Cálculo de las condiciones de remanso a la entrada, y esquema en un diagrama T-s de todos los procesos.

Ver figura: 0-1 compresión dinámica, 1-2 expansión en la turbina, 2-3 enfriamiento de los equipos, 3-4 compresión para evacuación del aire, que sale a p0=25 kPa

>	eqTt:=T1=T0+(v0^2/(2*c[p]));T1_:=subs(dat,rhs(%));eqpt:=p1=p0*(T1/T0)^(gamma/(gamma-1));p1_:=subs(T1=T1_,dat,rhs(%));

	(1)

i.e. las condiciones totales son T1=286 K (13 ºC) y 40 kPa.

b) Temperatura de salida de la turbina, en función de la presión de salida de esta (p2), y potencia generada. Aplicación para p2=15 kPa.

>

p2=p2;T2=T1*(1-eta[T]*(1-(p2/p1)^((gamma-1)/gamma)));T2_:=subs(T1=T1_,p1=p1_,dat,rhs(%));WdotT=m*c[p]*(T1-T2);WdotT_:=subs(dat,m*c[p]*(T1_-T2_));WdotT__:=subs(SI0,WdotT_);T2_15:=subs(p2=p2_15,dat,T2_);WdotT_15:=subs(p2=p2_15,dat,WdotT_);print(p1/p2,p2, T2,`WdotT=`);for i from 1 to 20 by 3 do p_:=p1_/(1+i/10);print(p1_/p_,p_*kPa_/(1000*Pa_),subs(p2=p_,dat,T2_),subs(p2=p_,dat,WdotT_)*kW_/(1000*W_));od:

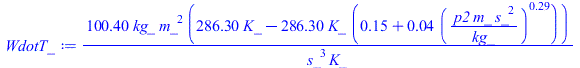	(2)

i.e. la potencia que da la turbina es WdotT=24433-1184·p2^0,286, en [W] si p2 está en [Pa]; si fuese p2=15 kPa, sería T2=227 K (-47 ºC) y la turbina produciría WdotT=6 kW.

Como el aire ha de salir del equipo a Teq-DT=50-50=0 ºC, i.e. T3=273 K y ha de absorber calor, tiene que entrar al equipo a T2<T3=273 K, luego la expansión ha de ser a <33 kPa (p1/p2>1.2

c) Determinar el valor de p2 para que el trabajo que produce la turbina iguale al que consume el compresor..

Sean 3 y 4 las condiciones totales de entrada y salida del compresor. Si suponemos que la velocidad de salida es pequeña, pt4=p4=p0, y como lo máximo que puede calentarse el aire al pasar por el equipo es hasta 50 ºC-50 ºC=0 ºC=272 K=T3, tenemos.

>

p3=p2;T3=Teq-DT;p4=p0;WdotT=WdotC;WdotC=m*c[p]*(T4-T3);T4=T3*(1+((p4/p3)^((gamma-1)/gamma)-1)/eta[C]);p3_:=p2;T3_:=subs(dat,Teq-DT);T4_:=subs(dat,T3_*(1+((p0/p2)^((gamma-1)/gamma)-1)/eta[C]));WdotC_:=subs(dat,m*c[p]*(T4_-T3_));WdotC__:=subs(SI0,WdotC_);for i from 1 to 20 by 3 do p_:=p1_/(1+i/10);print(p1_/p_,p_*kPa_/(1000*Pa_),subs(p2=p_,dat,T4_),subs(p2=p_,dat,WdotC_)*kW_/(1000*W_));od:eqBE:=subs(SI0,WdotT_=WdotC_);p2_:=fsolve(%,p2)*Pa_;T2_:=subs(p2=p2_,dat,T2_);T4_:=subs(p2=p2_,dat,T4_);'p1/p2'=p1_/p2_,'p4/p3'=subs(dat,p0/p2_);Wdot_=subs(p2=p2_,dat,WdotT_)*kW_/(1000*W_);

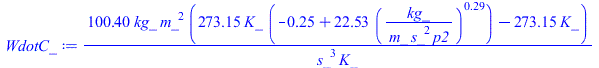	(3)

i.e. para que WdotT sea igual a WdotC ha de ser p2=13,6 kPa. Nótese que la ecuación (eqBE) es lineal en p2^0,286=x.

d) Calcular el calor evacuado del equipo.

>	Qdot=m*c[p]*(T3-T2);Qdot_=subs(dat,m*c[p]*(T3_-T2_))*kW_/(1000*W_);

	(4)

i.e. se extraen del equipo 5,2 kW de calor.

>