>	restart:#"m18_p45"

Para mantener un cierto local a 25 ºC, estando el aire exterior a 5 ºC, 94 kPa y 90% HR, se necesita aportar 3 kW, lo cual se piensa hacer con una bomba de calor, que usa R134a, funcionando con temperaturas de trabajo tales que el salto térmico mínimo en los cambiadores sea de 5 ºC, y con rendimiento del compresor del 65%. Se pide:

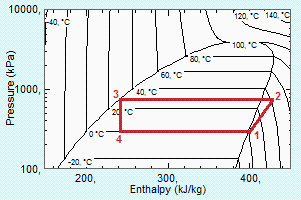
a) Esquema del proceso, y presiones y temperaturas en los diferentes estados del ciclo.

b) Potencia necesaria para la compresión, y gasto circulante de refrigerante.

c) Rendimientos energético y exergético (respecto a los datos de partida).

d) Estimar la cantidad máxima de agua condensada.

e) Si el flujo de aire que se hace pasar por el vaporizador de la máquina saliese a 1 ºC y no se alterase el ciclo del refrigerante, determinar la cantidad de agua condensada y el caudal de aire.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):with(RealDomain):

>	su1:="CF3CH2F":su2:="H2O":su3:="Aire":dat:=[QdotC=3e3*W_,Tl=(25+273.15)*K_,T0=(5+273.15)*K_,p0=94e3*Pa_,phi0=0.9,DT=5*K_,eta[C]=0.65,Tsa=(1+273.15)*K_];

>	Adat:=op(subs(T[b]=Tb,[get_gas_data(su3)])):Wdat:=get_gas_data(su2),get_liq_data(su2):pvW:=get_pv_data(su2):dat:=op(dat),get_gas_data(su1),get_liq_data(su1),Const,SI2,SI1:get_pv_data(su1):

a) Esquema del proceso, y presiones y temperaturas en los diferentes estados del ciclo.

Tomamos el ciclo simple en el que el compresor aspira vapor saturado (estado 1) y a la válvula entra líquido saturado (estado 3).

>

Tv1:=T0-DT;Tv1_:=subs(dat,%);'Tv1_'=TKC(%);pv1_:=subs(dat,evalf(subs(dat,pv(Tv1_))));Tv2:=Tl+DT;Tv2_:=subs(dat,%);'Tv2_'=TKC(%);pv2_:=subs(dat,evalf(subs(dat,pv(Tv2_))));p1_:=pv1_;T1='Tv1';T1_:=Tv1_;'T1_'=TKC(%);p2_:=pv2_;T2:=T1*(1+((p2/p1)^((gamma-1)/gamma)-1)/eta[C]);T2_:=subs(T1=T1_,p1=p1_,p2=p2_,dat,%);'T2_'=TKC(%);p3_:=p2_;T3:='Tv2';T3_:=Tv2_;'T3_'=TKC(%);p4:=pv1;T4='Tv1';

	(1)

i.e. sale vapor saturado del vaporizador a 0 ºC y 295 kPa (absoluta), que entra al compresor y sale a 41 ºC y 780 kPa; se enfría en el condensador hasta salir como líquido saturado a 30 ºC, pasando luego a la válvula de expansión y al vaporizador, completándose así el ciclo.

b) Potencia necesaria para la compresión, y gasto circulante de refrigerante.

Tomamos como origen de entalpías el líquido en el punto triple.

>	h1_:=subs(dat,T=T1_,dat,hv(T));h2_:=subs(dat,T=T2_,dat,hv(T));h3_:=subs(dat,T=T3_,dat,hl(T));h4_:=h3_;mdotR:=QdotC/(h2-h3);mdotR_:=subs(h2=h2_,h3=h3_,dat,%);WdotC:='mdotR'*(h2-h1);WdotC_:=subs(dat,mdotR_*(h2_-h1_));QdotR_:=subs(dat,mdotR_*(h1_-h3_));

	(2)

i.e. hay que hacer circular 0,015 kg/s de refrigerante, lo que consumirá una potencia de 490 W en el compresor.

c) Rendimiento energético y exergético (respecto a los datos de partida).

>	eqCOP:=eta[e]=QdotC/'WdotC';eqCOP_:=eta[e]=subs(dat,QdotC/WdotC_);eqCarnot:=eta[Carnot]=Tl/(Tl-T0);eqCarnot_:=subs(dat,%);eqX:=eta[x]=eta[e]/eta[Carnot];eqX_:=subs(eqCarnot_,eqCOP_,dat,%);

	(3)

i.e. la eficiencia energética es del 570% (se aporta al local 5,7 veces más energía de la que consume la máquina), y la eficiencia exergética del 38% del límite termodinámico.

Si en vez de con este modelo de sustancia perfecta se resuelve este problema con los mejores modelos disponibles (NIST), para los puntos clave (1 y 3) tenemos:

Liquid Vapor Liquid Vapor Liquid Vapor

Temperat. Pressure Density Density Enthalpy Enthalpy Entropy Entropy

(°C) (kPa) (kg/m³) (kg/m³) (kJ/kg) (kJ/kg) (kJ/kg-K) (kJ/kg-K)

(1) 0,0000 292,80 1294,8 14,428 200,00 398,60 1,0000 1,7271

(3) 30,000 770,20 1187,5 37,535 241,72 414,82 1,1435 1,7145

y para el estado 2:

Temperat. Pressure Density Enthalpy Entropy

(°C) (kPa) (kg/m³) (kJ/kg) (kJ/kg-K)

(1) 0,00000 292,80 14,428 398,60 1,7271

(2s) 33,643 770,20 36,678 418,66 1,7271

(2) 44,190 770,20 34,531 429,52 1,7619

con lo que mdotR=3/(429,5-241,7)=0,016 kg/s, WdotC=0,016*(429,4-398,6)=493 W, QdotR=3-0,49=2,51 kW. Como se ve, la desviación más importante es en el consumo del compresor, que en vez de 490 W es de 525 W.

>

d) Estimar la cantidad máxima de agua condensada.

Si toda la potencia de refrigeración se emplease en condensar agua:

>	mw_max:=Qdot/hlv;hlv_:=subs(Wdat,dat,h[lv0]-(c-c[p])*(T0-T[b]));mw_max_:=subs(dat,QdotR_/hlv_)*1000*g_/kg_;

	(4)

i.e. el caudal de agua condensado será menor de 1 g/s (<3,6 kg/h).

e) Si el flujo de aire que se hace pasar por el vaporizador de la máquina saliese a 1 ºC y no se alterase el ciclo del refrigerante, determinar la cantidad de agua condensada y el caudal de aire.

Al entrar tan húmedo es de suponer que salga saturado por debajo del punto de rocío:

>	eq8_9;eq8_11;eq8_8;pvW0:=pvW(subs(dat,T0));Tdew:=evalf(subs(dat,solve(pvW(T)=phi0*pvW0,T)));'Tdew'=TKC(%);

	(5)

En efecto, empieza a condensar (punto de rocío) a 3,5 ºC, luego a 1 ºC habrá condensado parte del vapor de agua.

Las humedades absolutas y las entalpías del aire húmedo, y los balances másico y energético, nos darán el gasto másico de aure y el de agua condensada:

>

w1_:=subs(Mva=subs(Wdat,M)/subs(Adat,M),phi=phi0,p[v](T)=pvW0,p=p0,dat,rhs(eq8_8));w2_:=evalf(subs(Mva=subs(Wdat,M)/subs(Adat,M),phi=1,p[v](T)=pvW(Tsa),p=p0,dat,rhs(eq8_8)));eqBMw:=ma*(w1-w2)=mw;eqBE:=ma*(h1a-h2a)=QdotR;h1a_:=subs(c[pa]=c[p],Adat,c[pv]=c[p],Wdat,T=T0,w=w1_,dat,rhs(eq8_11));h2a_:=subs(c[pa]=c[p],Adat,c[pv]=c[p],Wdat,T=Tsa,w=w2_,dat,rhs(eq8_11));ma_:=subs(dat,QdotR_/(h1a_-h2a_));mw_:=ma_*(w1_-w2_)*1000*g_/kg_;

	(6)

i.e. hay que soplar 0,40 kg/s de aire que entra con 5,3 g/kg de agua y sale con 4,4 g/kg, soltando 0,35 g/s (1,3 kg/h) de agua condensada (algo menos de la mitad del valor máximo antes calculado).

>