| > | restart:#"m18_p28" |
Un viejo refrigerador de R12 funciona con presiones de 150 kPa y 950 kPa, con un gasto másico de 10 kg/min y un rendimiento isentrópico de compresión del 70%. Se pide:
a) Esquema de componentes, diagramas p-h y T-s de los procesos, y fracción másica de vapor a la salida de la válvula.
b) Capacidad de refrigeración y temperatura mínima práctica de trabajo.
c) Rendimientos energético y exergético de la instalación.
Datos:
| > | read"../therm_eq.m":read"../therm_proc.m":with(therm_proc): |
| > | su:="CCl2F2":dat:=[mR12=(10/60)*kg_/s_,p1=150e3*Pa_,p2=950e3*Pa_,eta[C]=0.7]; |
Eqs. const.:
| > | dat:=op(dat),get_gas_data(su),get_liq_data(su),Const,SI2,SI1:R12data_M_cp_Tf_Tb_hlvb_c:=subs(dat,[M,c[p],T[f],T[b],h[lv0],c]);;get_pv_data(su): |
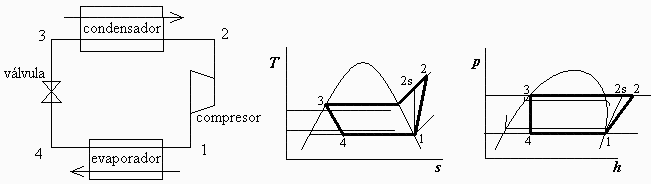
a) Esquema de componentes, diagramas p-h y T-s de los procesos, y fracción másica de vapor a la salida de la válvula.
(Ver diagramas arriba).
Se necesitan los valores de las entalpías. Los cálculos se pueden hacer tomando valores de un gráfico de datos del R12, pero aquí lo haremos analíticamente suponiendo válido el modelo de sustancia perfecta, que solo requiere unos pocos valores numéricos (seis) que se encuentran tabulados para muchas sustancias, en lugar de un gráfico específico para cada una..
Tomando como referencia h=s=0 para el líquido en el punto triple (cuya temperatura se aproxima por la del punto de congelación normal, Ttr=Tf; la pcr la obtendríamos con la relación de Antoine, pv(T), pero no hace falta):
| > | T1_:=subs(dat,evalf(subs(dat,solve(p1=pv(T),T))));'T1_'=TKC(%);T3_:=subs(dat,evalf(subs(dat,solve(p2=pv(T),T))));'T3_'=TKC(%);h3_:=subs(dat,subs(dat,T=T3_,hl(T)));eqBE34:=h3=(1-x4)*h4l+x4*h4v;h4v:=h1;h1_:=subs(dat,subs(dat,T=T1_,hv(T)));h4l_:=subs(dat,subs(dat,T=T1_,hl(T))):'h4l'=evalf(%,2);x4_:=(h3_-h4l_)/(h1_-h4l_); |
i.e., el compresor toma vapor de R12 a -20 ºC, y la salida del condensador es líquido saturado a 39 ºC. La fracción másica de vapor a la salida de la válvula es del 36 %.
b) Capacidad de refrigeración y temperatura mínima práctica de la carga
| > | Q41:=mR12*(h1-h4);Q41_:=subs(dat,mR12*(h1_-h3_)); |
i.e. el refrigerador es capaz de evacuar 17 kW de un sistema que esté a T>253 K (unos 258 K en la práctica para permitir una transmisión de calor efectiva).
c) Rendimientos energético y exergético de la instalación.
La temperatura del condensador es de 313 K, que es compatible con una temperatura ambiente hasta unos 308 K (35 ºC), para dejar al menos 5 ºC de salto térmico en los cambiadores. El rendimiento de una máquina de Carnot entre las temperaturas extremas, sin contar el sobrecalentamiento en el compresor, sería:
| > | eta[eC]:=T1/(T3-T1);eta[eC_]:=T1_/(T3_-T1_):'eta[eC]'=evalf(%,2);eta[eClim]:=(T1+5*K_)/(T3-T1-10*K_);eta[eClim_]:=(T1_+5*K_)/(T3_-T1_-10*K_):'eta[eClim]'=evalf(%); |
i.e. en el caso límite (Carnot) de evacuar calor de una T1 hasta una T2>T1, el rencimiento (COP) sería de 4,2 si es desde -20 ºC a 39 ºC, o de 5,2 si la carga estuviese a -15 ºC y el ambiente a 34 ºC.
Para el rendimiento energético real de la máquina de R134a:
| > | T2s:='T1*(p2/p1)^((gamma-1)/gamma)';'gamma'=subs(dat,gamma);T2s_:=subs(dat,T1_*(p2/p1)^((gamma-1)/gamma));h2s_:=subs(dat,subs(dat,T=T2s_,hv(T)));h2_:=subs(dat,h1_+(h2s_-h1_)/eta[C]);T2_:=subs(dat,T1_+(h2_-h1_)/c[p]);W12:=mR12*(h2-h1);W12_:=subs(dat,mR12*(h2_-h1_));eta[e]:='Q41/W12';eta[e_]:=Q41_/W12_:'eta[e]'=evalf(%);eta[x]:='eta[e]/eta[eClim]';eta[x_]:=eta[e_]/eta[eClim_]:'eta[x]'=evalf(%); |
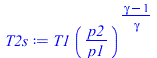 |
![`/`(`*`(eta[e]), `*`(eta[eClim]))](images/p281_30.gif) |
i.e. la màquina consume 8,5 kW, su rendimiento energético es 2,0, y su rendimiento exergético 0,39 (que indica que en el límite bastaría haber consumido un 39% de esos 8,5 kW).
Para estimar la bondad de la aproximación de gas perfecto, calculamos la corrección por el método de estados correspondientes (MEC).
| > | pR1:=p1/p[cr];pR1_:=subs(dat,p1/p[cr]);TR1:=T1/T[cr];TR1_:=subs(dat,T1_/T[cr]);Z1=0.95;pR2:=p2/p[cr];pR2_:=subs(dat,p2/p[cr]);TR2:=T2/T[cr];TR2_:=subs(dat,T2_/T[cr]);Z2=0.85; |
Bueno, estas serían la correciones en densidad respecto al modelo de gas ideal (rho=p/(ZRT)), y vemos que pueden llegar al 15 % (Z=0,85).
| > |