| > | restart:#"m17_p56" |
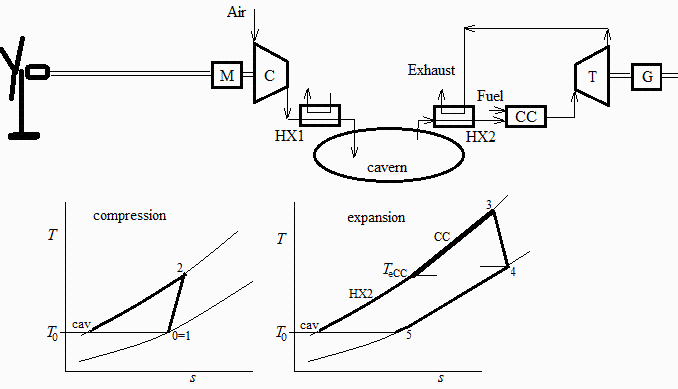
Para aprovechar los excesos de producción eléctrica de un parque eólico (la parte que no demanda la red en ese momento) se piensa utilizar un gran depósito subterráneo para almacenar aire comprimido. Para ello se usa un motor eléctrico M que mueve un compresor C. Éste, toma aire ambiente, lo comprime, lo pasa por un cambiador de calor al ambiente HX1, y lo inyecta en el depósito D. Cuando hace falta mayor producción eléctrica de la que dan los aerogeneradores, se extrae aire comprimido del depósito D, se pasa primero por un precalentador HX2, luego entra en una cámara de combustión CC con gas natural, luego entra a la turbina, y finalmente se hace pasar por el cambiador de calor HX2 para precalentar el aire extraído. Supóngase que el depósito se mantiene a 3 MPa, que los rendimientos del compresor, la turbina, y el cambiador de calor HX2, son del 85 %, 90 %, y 70 %, respectivamente, y que la temperatura máxima de entrada a la turbina es 1500 K. Se pide:
a) Rendimiento exergético del proceso de compresión, i.e. exergía almacenada en el aire comprimido del depósito respecto al consumo eléctrico necesario.
b) Esquema de la instalación, y de los procesos de compresión y de producción (diagrama T-s).
c) Temperatura de salida de la turbina, y de entrada a la cámara de combustión.
d) Trabajos unitarios de la turbina y consumo de gas natural.
e) Rendimiento térmico de la generación de potencia con la turbina, y rendimiento térmico global teniendo en cuenta el proceso de compresión.
Datos:
| > | read`../therm_chem.m`:with(therm_chem):with(therm_proc): |
| > | su1:="Aire":su2:="C4":dat:=[p2=3e6*Pa_,eta[C]=0.85,eta[T]=0.90,eta[HX2]=0.7,T3=1500*K_]; |
| > | dat:=op(dat),get_gas_data(su1),Const,SI2,SI1: |
a) Rendimiento exergético del proceso de compresión, i.e. exergía almacenada en el aire comprimido del depósito respecto al consumo eléctrico necesario.
La energía consumida por el compresor, y la exergía de flujo del aire comprimido a 3 MPa y T0=15 ºC, son:
| > | eqBEC:=wC=c[p]*(T2-T1);eq5_59;eqBEC:=wC=c[p]*T0*(((p2/p1)^((gamma-1)/gamma)-1)/eta[C]);eqBEC_:=subs(p1=p0,dat,%);eqpsi:=psi=(h-h0)-T0*(s-s0);eqpsi:=psi=c[p]*(T-T0)-T0*(c[p]*ln(T/T0)-R*ln(p/p0));T=T0;eqpsi:=psi=R*T0*ln(p2/p0);eqpsi_:=subs(dat,evalf(subs(dat,%)));eqeta:=eta[xC]=psi/w;eqeta:=eta[xC]=subs(eqpsi,eqBEC,psi/wC);eqeta:=evalf(subs(p1=p0,dat,%)); |
![eta = `/`(`*`(`+`(`^`(pi[12], `/`(`*`(`+`(gamma, `-`(1))), `*`(gamma))), `-`(1))), `*`(`+`(`/`(`*`(T2), `*`(T1)), `-`(1))))](images/p561_4.gif) |
|
![wC = `/`(`*`(c[p], `*`(T0, `*`(`+`(`^`(`/`(`*`(p2), `*`(p1)), `/`(`*`(`+`(gamma, `-`(1))), `*`(gamma))), `-`(1))))), `*`(eta[C]))](images/p561_5.gif) |
|
![eta[xC] = `/`(`*`(R, `*`(ln(`/`(`*`(p2), `*`(p0))), `*`(eta[C]))), `*`(c[p], `*`(`+`(`^`(`/`(`*`(p2), `*`(p1)), `/`(`*`(`+`(gamma, `-`(1))), `*`(gamma))), `-`(1)))))](images/p561_13.gif) |
|
| (1) |
i.e. el rendimiento exergético es del 50 %, lo que significa que, como máximo, podremos recuperar el 50 % de la electricidad sobrante en el parque eólico.
El interés de disponer así el HX1 es escaso, pues el aire comprimido inyectado acabará atemperándose; solo sería útil si se quisiera aprovechar ese calor (e.g. para obtener agua caliente).
b) Esquema de la instalación, y de los procesos de compresión y de producción (diagrama T-s).
(Ver arriba.)
c) Temperatura de salida de la turbina, y de entrada a la cámara de combustión.
El HX2 es un recuperador de calor gas/gas, así que no será muy bueno el modelo ideal de caída despreciable de presión y contacto prolongado hasta igualar temperaturas. Resolveremos primero con el límite ideal, y compararemos después con un valor razonable del rendimiento del HX2 del 70 %.
La entrada a la turbina es a 3 MPa y 1400 K, y la salida a presión ambiente y temperatura T4. La temperatura de entrada a la CC, TeCC, se obtiene del rendimiento del cambiador HX2.
| > | eq5_60;eq5_62;T4_:=subs(p3=p2,p4=p0,dat,rhs(%));'T4_'=TKC(%);eqHX:=eta[HX2]=(TeCC-T0)/(T4-T0);eta[HX2]=1;TeCC_:=subs(T4=T4_,dat,solve(1=rhs(eqHX),TeCC));'TeCC_'=TKC(%);eta[HX2]=subs(dat,eta[HX2]);TeCC__:=subs(T4=T4_,dat,solve(eqHX,TeCC));'TeCC__'=TKC(%); |
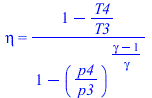 |
|
![T4 = `*`(T3, `*`(`+`(1, `-`(`*`(eta[T], `*`(`+`(1, `-`(`^`(`/`(`*`(p4), `*`(p3)), `/`(`*`(`+`(gamma, `-`(1))), `*`(gamma)))))))))))](images/p561_16.gif) |
|
| (2) |
i.e. el aire que se extrae del depósito a T0=15 ºC, se calienta con los gases de escape de la turbina hasta 388 ºC (o solo hasta 276 ºC si etaHX2=0,7) y luego se quema con CH4 hasta alcanzar los 1500 K de entrada a la turbina, de la que salen los gases a T4=388 ºC.
d) Trabajos unitarios de la turbina y consumo de gas natural.
| > | eqBET:=wT=c[p]*(T3-T4);eqBET:=wT=c[p]*T3*(eta[T]*(1-(p0/p2)^((gamma-1)/gamma)));eqBET_:=subs(dat,%);eqBECC:=mf*PCI=ma*c[p]*(T3-TeCC);mf_ma:=c[p]*(T3-TeCC)/PCI;eqE:=CH4+2*O2=CO2+2*H2O;PCI_:=PCI(eqE);eqM:=Mf(CH4);PCIm_:=PCI_/rhs(eqM);mf_ma_:=subs(dat,c[p]*(T3-TeCC_)/PCIm_); |
![wT = `*`(c[p], `*`(T3, `*`(eta[T], `*`(`+`(1, `-`(`^`(`/`(`*`(p0), `*`(p2)), `/`(`*`(`+`(gamma, `-`(1))), `*`(gamma)))))))))](images/p561_27.gif) |
|
| (3) |
i.e., la turbina genera 842 kJ/kg (842 kW por cada kg/s de gases turbinados), a expensas del aire comprimido y de una inyección de 0,019 kg de gas natural por cada kg de aire.
e) Rendimiento térmico de la generación de potencia con la turbina, y rendimiento térmico global teniendo en cuenta el proceso de compresión.
Del diagrama T-s se deduce que, si el HX2 es ideal, la potencia mecánica generada por la turbina sería igual a la potencia térmica comunicada al aire en la cámara de combustión (modelo de aire estándar):
| > | eqeta:=eta[th]=wT/qCC;eqeta:=eta[th]=wT/(c[p]*(T3-TeCC));eqeta_:=subs(eqBET,TeCC=TeCC_,dat,%); |
| (4) |
Incluso con un rendimiento normal del HX2 (e.g. del 70 %), el valor anterior del rendimiento de la turbina sería del 88 %, que sigue siendo muy superior a los valores normales. La explicación es que este rendimiento no tiene en cuenta que se parte ya del aire comprimido, no de aire ambiente; si se considera globalmente, incluyendo el compresor, vemos que el rendimiento térmico no es tan bueno:
| > | eqetaG:=eta[th_global]=(wT-wC)/qCC;eqetaG:=eta[th_global]=subs(eqBET_,eqBEC_,TeCC=TeCC_,dat,(wT-wC)/(c[p]*(T3-TeCC))); |
| (5) |
i.e. el rendimiento neto es del 34 % (30 % con etaHX2=0,7), bastante bajo para una central convencional de potencia (que casi alcanza el 60 % si es de ciclo combinado), pero el compresor no detrae trabajo de la turbina porque consume electricidad sobrante del parque eólico, que de otra forma no se aprovecharía para nada.
NOTA. Estos sistemas de almacenamiento energético (CAES, compressed air energy storage) están muy poco desarrollados, entre otras razones porque las variaciones de presión en las cavernas pueden producir movimientos sísmicos como los que se manifestaron en el de almacenamiento de gas natural.
| > |