>	restart:#"m17_p44"

Considérese una planta de potencia que usa n-butano como fluido de trabajo siguiendo un ciclo Rankine, en el que una bomba toma butano líquido del condensador, lo hace pasar por el vaporizador, que aprovecha un flujo de 10 kg/s de agua salobre a presión y 120 ºC procedente de un manantial geotérmico, y luego por una turbina al condensador, cerrándose el ciclo. Suponiendo que en los cambiadores de calor ha de haber un salto mínimo de 5 ºC de un lado al otro, que la vaporización es a 100 ºC, y que los rendimientos isentrópicos de bomba y turbina son del 75%, se pide:
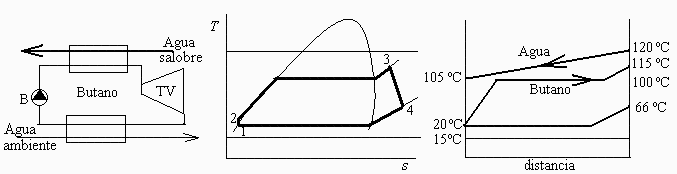
a) Esquema de la instalación y de los procesos en un diagrama T-s.
b) Estado del fluido a la entrada de la turbina.
c) Estado del fluido a la salida de la turbina.
d) Rendimiento energético de la planta.
e) Esquema de los perfiles de temperatura en los cambiadores de calor.
f) Potencia producida.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su1:="C4H10":su2:="H2O":dat:=[mw=10*kg_/s_,Tw=(120+273.15)*K_,DT=5*K_,Tv=(100+273.15)*K_,eta=0.75];

Eqs. const.:

>	dat:=op(dat),get_gas_data(su1),get_liq_data(su1),Const,SI2,SI1:get_pv_data(su1):Wdat:=get_liq_data(su2):

a) Esquema de la instalación y de los procesos en un diagrama T-s.

(Ver arriba.)

b) Estado del fluido a la entrada de la turbina.

Lo máximo que se podrá calentar el vapor de n-butano es hasta los 5 ºC por debajo de la temperatura de entrada del agua salobre: 120-5=115 ºC y la presión será la de vaporización a 100 ºC.

>	eqDT:=T3=Tw-DT;T3_:=subs(dat,Tw-DT);'T3'=TKC(%);eqvap:=p3=p[v](T[v]);p3_:=subs(dat,evalf(subs(dat,pv(Tv))));

i.e. entra a la turbina a 115 ºC y 1,5 MPa.

c) Estado del fluido a la salida de la turbina.

La presión de salida será la de condensación a 5 ºC por encima de la ambiente, que supondremos a 288 K; i.e. pv(293 K).

>	eqp4:=p4=p[v](T0+DT);Tv4_:=subs(dat,T0+DT);'Tv4_'=TKC(%);;p4_:=subs(dat,evalf(subs(dat,pv(T0+DT))));

Para la temperatura, empecemos suponiendo que no condensa. Con el modelo de gas perfecto:

>	eqeta:=eta[T]=(1-T4/T3)/(1-(p4/p3)^((gamma-1)/gamma));eqg:=gamma=c[p]/(c[p]-R);c[p]=subs(dat,c[p]);gamma=subs(dat,gamma);T4_:=subs(eta[T]=eta,T3=T3_,p3=p3_,p4=p4_,dat,solve(eqeta,T4));'T4_'=TKC(%);

i.e. como saldría a 67 ºC, que es más de los 20 ºC de saturación a esa presión, se trata de vapor sobrecalentado y es válida la suposición.

d) Rendimiento energético de la planta.

>	h1_:=subs(dat,T=Tv4_,dat,hl(T));h2_:=h1_;h3_:=subs(dat,T=T3_,dat,hv(T));h4_:=subs(dat,T=T4_,dat,hv(T));eqetae:=eta[e]=(h3-h4)/(h3-h2);eqetae:=eta[e]=(h3_-h4_)/(h3_-h2_);

El rendimiento es bajo, como es de esperar para estos ciclos de vapor con tan poco salto térmico.

e) Esquema de los perfiles de temperatura en los cambiadores de calor.

Lo más importante es garantizar que no hay 'cruce de temperaturas', i.e. que el acercamiento máximo es inferior a 5 ºC, por lo que apenas se podrá aprovechar el agua salobre por debajo de los 105 ºC.

Si suponemos que el agua sale a Tv+DT=100+5=105 ºC como se indica en la figura, el calor extraído del agua y el gasto de n-butano vaporizado serían:

>	eqBE:=mw*c*(Twin-Twout)=mB*(h3-h2);Twin:=subs(dat,Tw);Twout:=Tv+DT;Twout_:=subs(dat,%);Qw:='mw*c*(Twin-Twout)';Qw_:=subs(Wdat,dat,%);mB_:=subs(Wdat,h3=h3_,h2=h2_,dat,solve(eqBE,mB));

	(1)

i.e. se extraen 627 kW de calor del agua, circulando 1,26 kg/s de n-butano. El acercamiento en el punto en que empieza a vaporizarse el n-butano (pitch point) , que será algo mayor, resulta:

>	QdotP:=mB*(h3-h2P);h2P_:=subs(dat,T=Tv,dat,hl(T));QdotP_:=subs(dat,mB_*(h3_-h2P_));TwP:=Tw-QdotP/(mw*c);TwP_:=subs(Wdat,dat,Tw-QdotP_/(mw*c));'TwP_'=TKC(%);DT_pitch:='TwP-Tv';DT_pitch_:=subs(dat,TwP_-Tv);

	(2)

i.e. casi 11 ºC. Se podría mejorar el rendimiento si se fija este acercamiento en el pitch point igual a 5 ºC y se calcula el gasto máximo de n-butano vaporizable, y el calor máximo extraíble con esta configuración:

>	TwP:=Tv+DT;TwP_:=subs(dat,%);eqBEv:='mw*c*(Tw-TwP)'=mB*(h3-h2P);mBmax_:=subs(Wdat,h3=h3_,h2P=h2P_,dat,solve(eqBEv,mB));Twout_min:=Tv-mBmax*c*(Tv-Tv4)/(mw*c);Twout_min_:=subs(mBmax=mBmax_,Tv4=Tv4_,Wdat,dat,%);'Twout_min_'=TKC(%);Qw_max:=subs(Wdat,dat,mw*c*(Twin-Twout_min_));

	(3)

i.e. el límite es aprovechar 1,52 MW del agua (en vez de los 627 kW antes calculados), y vaporizar 2,06 kg/s de n-butano (en vez de los 1,2 kg/s anteriores).

f) Potencia producida.

Extrayendo 1,52 MW del agua, la turbina de vapor generaría 157 kW. Con los valores previous de mB=1,26 kg/s y Qw=627 kW, se generarían solo 96 kW.

>	Wdot:='mBmax*(h3-h4)';Wdot_:=subs(dat,mBmax_*(h3_-h4_));

	(4)

Conviene comparar este valor con el límite termodinámico (la exergía del manantial). Como es costumbre, solo se contempla la exería termomecánica, no la química.

>	Wdotmax:=mw*(Dh-T0*Ds);Wdotmax:=mw*(c*(Tw-T0)-T0*c*ln(Tw/T0));Wdotmax_:=subs(dat,evalf(subs(Wdat,dat,%)));

	(5)

i.e. el límite (inalcanzable) es de 647 kW de potencia producible, y con esta instalación se generan 157 kW.

>

ADICIONAL

Para conocer la bondad del modelo de sustancias perfectas aquí usado para resolver este ejercicio, se presenta a continuación la solución primera, i.e. la que suponía una Twout=105 ºC, usando el modelo más preciso disponible (NIST):

>

p3_:=1522e3*Pa_;p4_:=207e3*Pa_;h1_:=48.3e3*J_/kg_;h2_:=h1_:h3_:=548.1e3*J_/kg_;s3_:=1.572e3*J_/(kg_*K_);T3s_:=318.5*K_;h4s_:=460.9e3*J_/kg_;h4_:=h3_-subs(dat,eta)*(h3_-h4s_);eqetae:=eta[e]=(h3_-h4_)/(h3_-h2_);mB_:=subs(Wdat,h3=h3_,h2=h2_,dat,solve(eqBE,mB));Qdot_:=subs(dat,mB_*(h3_-h2_));Wdot_:=subs(dat,mB_*(h3_-h4_));

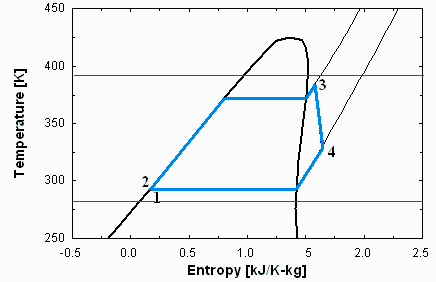
i.e. el rendimiento no sería del 15% sino del 13%, y solo se puede generar 82 kW en vez de 96 kW (hemos retenido para el agua el modelo perfecto). Y el diagrama T-s a escala es:

>