>	restart:#"m17_p42"

Para generar trabajo a partir de la radiación solar, se va a considerar una máquina que usa dióxido de carbono  en un ciclo supercrítico que funciona de la manera siguiente: con una bomba de rendimiento isentrópico del 85%, se hace pasar líquido desde el estado saturado en el condensador, hasta introducilo a 20 MPa en el captador solar, donde se calienta a presión constante hasta 150 ºC; a continuación pasa por una turbina de rendimiento isentrópico del 80%, y luego es condensado con agua ambiente a 20 ºC, con un salto térmico mínimo de 2 ºC, cerrándose el ciclo. Se pide:
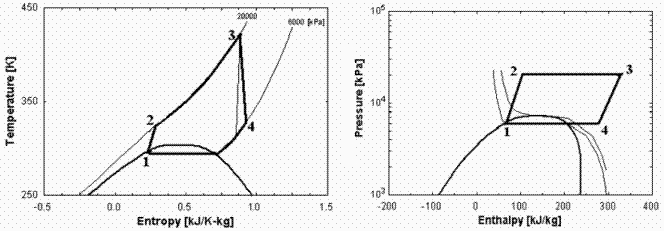
a) Hacer un esquema de los procesos en los diagramas T-s y p-h.
b) Determinar los estados termodinámicos principales del fluido de trabajo en el ciclo.
c) Calcular el rendimiento energético del ciclo.
d) Calcular el gasto másico necesario para generar 1 kW.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su:="CO2":dat:=[p2=20e6*Pa_,eta[B]=0.85,T3=(150+273.15)*K_,eta[T]=0.80,T0=(20+273.15)*K_,DT=2*K_,Wdot=1e3*W_];

Eqs. const.:

>	dat:=op(dat),get_gas_data(su),get_liq_data(su),Const,SI2,SI1:get_pv_data(su):

a) Hacer un esquema de los procesos en un diagrama T-s.

Ver figura arriba (obtenida con el programa TermoPro del NIST).

>	T1:=T0+DT;T1_:=subs(dat,T1);p1_:=subs(dat,evalf(subs(dat,pv(T1_))));pcr:=subs(dat,p[cr]);

efectivamente, el ciclo tiene la presión de alta (20 MPa) superior a la crítica (7,4 MPa).

b) Determinar los estados termodinámicos principales del fluido de trabajo en el ciclo.

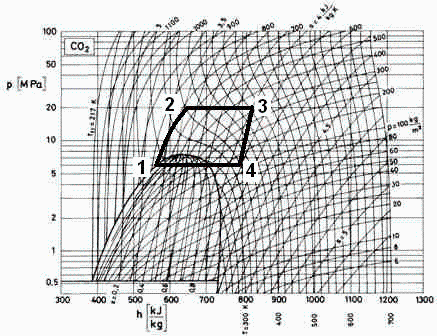
No vale el modelo de sustancia perfecta porque estamos cerca de la región crítica; según se aprecia en el diagrama p-h del CO2, disponible.

Según este último diagrama (las h y s dependen de la referencia elegida, que puede cambiar de un diagrama a otro):

El punto 1 será el de líquido saturado a (20+5) ºC: p1=6 MPa, h1=560 kJ/kg, s1=3,3 kJ/(kg·K).

El punto 2s estará en la misma isentrópica y a 20 MPa: h2s=580 kJ/kg.

El punto 2 vendrá dado por el rendimiento de la bomba: h2=h1+(h2s-h1)/eta=584 kJ/kg.

El punto 3 es dato: 20 MPa y 150 ºC: h3=820 kJ/kg.

El punto 4s estará en la misma isentrópica y a 6 MPa: h4s=760 kJ/kg.

El punto 4 vendrá dado por el rendimiento de la turbina: h4=h3-eta(h3-h2s)=770 kJ/kg.

>	h1:=560e3*J_/kg_;h2s:=580e3*J_/kg_;eqetaB:=eta[B]=Ws/W;eqetaB:=eta[B]='(h2s-h1)/(h2-h1)';h2:=h1+(h2s-h1)/subs(dat,eta[B]);h3:=820e3*J_/kg_;h4s:=760e3*J_/kg_;eqetaT:=eta[T]=W/Ws;eqetaT:=eta[T]='(h3-h4)/(h3-h4s)';h4:=h3-(h3-h4s)*subs(dat,eta[T]);

c) Calcular el rendimiento energético del ciclo.

>	eqeta:=eta=Wnet/Qpos;Wnet:='(h3-h4)-(h2-h1)';Qpos:='h3-h2';eqeta_:=eqeta;

i.e. por cada julio absorbido del sol, se generan 0,1 julios de trabajo. Aunque el rendimiento parece demasiado bajo en comparación con los motores térmicos usuales (eta=0,3..0,4), no está mal para un motor solar de baja temperatura. Más problemático resultariá conseguir funcionar con tan altas presiones, y con un salto térmico tan pequeño (el condensador costaría mucho e introduciría mucha pérdida de carga).

d) Calcular el gasto másico necesario para generar 1 kW.

>	eqW:=Wdot='mCO2*wnet';eqW:=Wdot='mCO2*((h3-h4)-(h2-h1))';mCO2_:=subs(dat,solve(%,mCO2));

i.e. hay que bombear 40 g/s de CO2 (lo cual se debería hacer, en vista de las grandes presiones, con una bomba desplazamiento positivo). desplazamiento positivo.

Con los datos del NIST,

>

h1:=63.05e3*J_/kg_;h2s:=80.58e3*J_/kg_;eqetaB:=eta[B]=Ws/W;eqetaB:=eta[B]='(h2s-h1)/(h2-h1)';h2:=h1+(h2s-h1)/subs(dat,eta[B]);h3:=324.7e3*J_/kg_;h4s:=263.8e3*J_/kg_;eqetaT:=eta[T]=W/Ws;eqetaT:=eta[T]='(h3-h4)/(h3-h4s)';h4:=h3-(h3-h4s)*subs(dat,eta[T]);eqeta:=eta=Wnet/Qpos;Wnet:='(h3-h4)-(h2-h1)';Qpos:='h3-h2';eqeta_:=eqeta;eqW:=Wdot='mCO2*wnet';eqW:=Wdot='mCO2*((h3-h4)-(h2-h1))';mCO2_:=subs(dat,solve(%,mCO2));

i.e. el rendimiento pasa del 10% obtenido antes (mirando el gráfico a ojo), al 12% que da el programa del NIST, y en vez de 40 g/s, hay que bombear sólo 36 g/s.

>