>	restart:#"m16_p30"

>	read`../therm_chem.m`:with(therm_chem);with(therm_proc):

Dentro de un tubo horizontal de 2 m de longitud y 2 cm de diámetro se ha preparado una mezcla de gas natural con aire estequiométrico, en equilibrio termomecánico con el ambiente. En un instante dado, se dejan abiertos los dos extremos del tubo y se provoca una chispa en el centro. Se pide:
a) Indicar cómo se propagaría la llama.
b) Determinar la composición de los gases frescos y de los quemados.
c) Calcular la temperatura de combustión adiabática.
d) Calcular la velocidad aparente de la llama.

Datos:

>	su1:="Aire":su2:="H2O":fuel:=CH4:dat:=[Lt=2*m_,L=1*m_,D=0.02*m_];

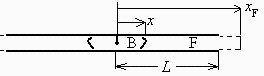
Eqs. const.:

>	Adat:=get_gas_data(su1):Wdat:=get_gas_data(su2),get_liq_data(su2):get_pv_data(su2):dat:=op(dat),op(subs(g=g0,[Const])),Adat,SI2,SI1:

a) Indicar cómo se propagaría la llama.

Se propagaría dos llamas simétricamente. No serían planas sino 'con morro', por el efecto de las paredes.

b) Determinar la composición de los gases frescos y de los quemados.

Inicialmente hay una mezcla estequiométrica de aire y gas natural (supondremos metano puro), a presión y temperatura ambientes.

>	eq15_2;eqA0_:=Ateo(fuel);eqET:=p0*V0=n0*R[u]*T0;eqET:=p0*L*Pi*D^2/4=n0*R[u]*T0;n0_:=evalf(subs(dat,solve(%,n0)));n0=nf*(1+A[0]);nf_:=n0_/(1+rhs(eqA0_));Inicial:=[x[CH4]=nf/n0,x[O2]=c21*A[0]*nf/n0,x[N2]=c79*A[0]*nf/n0];Inicial_:=subs(A[0]=rhs(eqA0_),nf=nf_,n0=n0_,dat,%);

Tras la combustión habrá:

>	eq:=eqMIX(a*fuel+a*A[0]*(c21*O2+c79*N2)=[2,3,4,6]);eqNX;eqBC;eqBH;eqBO;eqBN;sol1:=subs(A[0]=rhs(eqA0_),dat,solve({eqNX,eqBC,eqBH,eqBO,eqBN},{a,x[Comp[2]],x[Comp[3]],x[Comp[4]],x[Comp[5]]}));

c) Calcular la temperatura de combustión adiabática.

Como el proceso es a presión constante:

>	eq15_7_2;eq15_5;PCI_:=subs(sol1,PCI(eq)/a);Ta_:=subs(sol1,cpComp,dat,rhs(eqTa));

d) Calcular la velocidad aparente de la llama.

Como el problema es simétrico, resolveremos sólo un lado (ver figura). Sea x(t) la posición de la llama, y xF(t) la posición imaginaria que ocuparía el final de los gases frescos si no se difundieran al salir.

>	eqET_t0:=p0*L*Pi*D^2/4=nf0*(1+A)*R[u]*T0;eqET_t_Burnt:=p0*x*Pi*D^2/4=(nf0-nf)*(1+A)*R[u]*TB;eqET_t_Fresh:=p0*(xF-x)*Pi*D^2/4=nf*(1+A)*R[u]*T0;

Dividiendo por eqET_t0 y derivando respecto al tiempo:

>	eqET_t_Burnt:=xdot/L=(-nfdor/nf0)*(TB/T0);eqET_t_Fresh:=xFdot/L-xdot/L=nfdot/nf0;

y eliminando nfdot, y como se sabe que la velocidad de deflagración laminar es la de la llama respecto a los gases frescos quietos:

>	eqVL:=VL=xdot-xFdot;eqET_t:=xdot/L=(VL/L)*(TB/T0);