Considérese un disco delgado de 1 m de diámetro, pintado de blanco por ambas caras, y enfrentado al Sol en una órbita halo alrededor del punto de Lagrange posterior del sistema Sol-Tierra (SEL2, a 1,5·106 km), sin interacción térmica más que con la radiación de fondo del Universo y el Sol (i.e. sin eclipses). Se pide:
a) Temperatura de equilibrio del disco, y valor de los términos del balance energético
b) Detrás hay otro disco del mismo diámetro, pintado de negro por ambas caras, paralelo y concéntrico con el anterior, a una distancia de 0,1 m. Determinar las temperaturas de equilibrio de cada disco en el límite de discos muy próximos (con valores típicos de pintura negra).
c) Resolver el caso anterior con la separación finita dada.
d) Valor de cada término de los balances energéticos.
Datos:
| > |
with(RealDomain):read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):assume(h_>0,r>0): |
| > |
dat:=[D=1*m_,L2ua=1.01,alpha1=0.2,epsilon1=0.85,L=0.1*m_,E=1361*W_/m_^2,Tinf=0*2.7*K_,alpha2=0.9,epsilon2=0.9];dat:=op(dat),Const,SI2,SI1: |
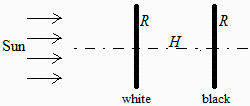
a) Temperatura de equilibrio del disco, y valor de los términos del balance energético.
La irradiancia solar E decae con r2. Si se considera una distancia media Sol-Tierra de 150·10^6 km (i.e. cerca de los equinoccios) con E=1361 W/m2, la irradiancia solar en SEL2 será 1361/1,01^2=1334 W/m2, y ese será el valor que tomemos (SEL2 a 1,01 ua). Nótese, sin embargo, que el perihelio terrestre es a 147·10^6 km y el afelio a 152·10^6 km, por lo que el SEL2 está a 0,99 ua en el perihelio y a 1,03 ua en el afelio, y las irradiaciones respectivas serían de 1380 W/m2 y de 1290 W/m2.
Los valores termoópticos se han tomado de las Tablas.
| > |
EL2=E/L2ua^2;EL2_:=subs(dat,E/L2ua^2);eqBE:=alpha1*A*EL2=2*epsilon1*A*sigma*T^4;A=Pi*D^2/4;A_:=evalf(subs(dat,Pi*D^2/4));Qs:=subs(A=A_,dat,alpha1*A*E/L2ua^2);T1:=simplify(sqrt(sqrt(alpha1*A*'EL2'/(2*epsilon1*A*sigma))));T1_:=evalf(subs(EL2=EL2_,dat,SI0,%))*K_;'T1_'=TKC(%);Q1inf1:=epsilon1*A*sigma*T1^4;Q1inf1_:=subs(A=Pi*D^2/4,EL2=EL2_,T1=T1_,dat,Q1inf1);T1:='T1': |
i.e. el disco quedaría a 229 K (-44 ºC), bastante frío porque absorbe poco por la cara soleada (Qs=210 W), y emite mucho por las dos (Qinf=105 W por cada una). Si fuera cuerpo negro quedaría a 329 K (56 ºC).
b) Detrás hay otro disco del mismo diámetro, pintado de negro por ambas caras, paralelo y concéntrico con el anterior, a una distancia de 0,1 m. Determinar las temperaturas de equilibrio de cada disco en el límite de discos muy próximos (con valores típicos de pintura negra).
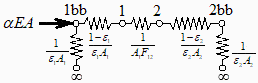
Sea 2 el disco negro. En el límite de discos muy próximos se trata de un recinto de dos nodos, con el siguiente circuito eléctrico equivalente (tomaremos M3=Minf=sigma*Tinf^4=0) y la conocida ecuación para Q12:
| > |
eqBE1:=alpha1*A*EL2-epsilon1*A*M1bb=Q12;subs(Q=Q12,eq13_6);A1=A2;F12=1;Q12:=A*(M1bb-M2bb)/(1/epsilon1+1/epsilon2-1);eqBE2:='Q12'=epsilon2*A*M2bb;sol:=solve(subs(Q21=-Q12,M3=0,{eqBE1,eqBE2}),{M1bb,M2bb});sol_:=subs(EL2=EL2_,dat,sol);T1_:=subs(sol_,dat,SI0,(M1bb/sigma)^0.25)*K_;'T1_'=TKC(%);T2_:=subs(sol_,dat,SI0,(M2bb/sigma)^0.25)*K_;'T2_'=TKC(%); |
i.e. con el disco negro trasero, en el límite F12=1, el disco 1 quedaría a 247 K en vez de a 229 K, y el disco 2 quedaría 204 K.
Si se toma el disco negro como radiador perfecto, en el límite F12=1 y epsilon2=1, el disco 1 quedaría a 245 K en vez de a 229 K, y el disco 2 quedaría 202 K.
NOTA. Puede parecer sorprendente que, habiendo supuesto que los dos discos están casi juntos, tengan diferente temperatura. La explicación es que la transmisión de calor por radiación entre placas infinitas tiene una resistencia térmica R=DT/Q finita, aunque tiende a infinito cuando epsilon tiende a cero. En términos de emitancia-bb, según la expresión de Q anterior, tomando iguales emisividades para simplificar, la resistencia es Re=DMbb/Q=(2-epsilon)/(epsilon*A), con un valor mínimo para cuerpos negros, Re=DM/Q=1/A, mientras que si el acoplamiento fuese conductivo sería R=DT/Q=L/(kA) y se podría hacer tender a cero con L=0 o con k=inf.
c) Resolver el caso anterior con la separación finita dada
Hay que recurrir al método de las exitancias, LNM, y calcular los factores de vista.
| > |
eqF:=F12=1+(1-sqrt(4*r^2+1))/(2*r^2);eqr:=r=R/H;eqr_:=r=subs(dat,D/(2*L));F12_:=evalf(subs(eqr_,rhs(eqF)));F13_:=1-F12_; |
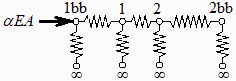
i.e. el 82 % de la radiación emergente de la parte trasera del disco 1 incide sobre el disco 2, y el otro 18 % va al vacío de fondo. El esquema eléctrico equivalente y las ecuaciones nodales son ahora:
| > |
eq1bb:=alpha1*A1*EL2=epsilon1*A1*(M1bb-M1)/(1-epsilon1)+epsilon1*A1*(M1bb-M3);eq1:=epsilon1*A1*(M1bb-M1)/(1-epsilon1)=A1*F12*(M1-M2)+A1*F13*(M1-M3);eq2:=A1*F12*(M1-M2)=A2*F23*(M2-M3)+epsilon2*A2*(M2-M2bb)/(1-epsilon2);eq2bb:=epsilon2*A2*(M2-M2bb)/(1-epsilon2)=epsilon2*A2*(M2bb-M3);eq1bb_:=subs(EL2=EL2_,A1=A_,A2=A_,F21=F12,F23=F13,F12=F12_,F13=F13_,M3=0,dat,SI0,eq1bb);eq1_:=subs(EL2=EL2_,A1=A_,A2=A_,F21=F12,F23=F13,F12=F12_,F13=F13_,M3=0,dat,SI0,eq1);eq2_:=subs(EL2=EL2_,A1=A_,A2=A_,F21=F12,F23=F13,F12=F12_,F13=F13_,M3=0,dat,SI0,eq2);eq2bb_:=subs(EL2=EL2_,A1=A_,A2=A_,F21=F12,F23=F13,F12=F12_,F13=F13_,M3=0,dat,SI0,eq2bb);sol_:=solve({eq1bb_,eq1_,eq2_,eq2bb_});T1_:=sqrt(sqrt(subs(sol_,dat,SI0,M1bb/sigma)))*K_;'T1_'=TKC(%);T2_:=sqrt(sqrt(subs(sol_,dat,SI0,M2bb/sigma)))*K_;'T2_'=TKC(%); |
i.e. con F12=0,82 y epsilon2=0,9, queda T1=240 K (en vez de 247 K) y T2=187 K en vez de 204 K.
d) Valor de todos los términos de los balances energéticos.
Disco delantero (blanco; e=exterior, i=interior):
| > |
Q1s:=alpha1*A*EL2;Q1s_:=Qs;Q1e:=epsilon1*A*M1bb;Q1e_:=subs(sol_,A=A_,dat,SI0,%)*W_;Q1i2:=A1*F12*(M1-M2);Q1i2_:=subs(sol_,A1=A_,F12=F12_,dat,SI0,%)*W_;Q1i3:=A1*F13*(M1-M3);Q1i3_:=subs(sol_,A1=A_,F13=F13_,M3=0,dat,SI0,%)*W_; |
i.e. el disco delantero (blanco) absorbe Q1s=alpha1*E*A=210 W, evacuando por delante 126 W al vacío, y los otros 84 hacia atrás: 60 W con el disco 2 más 24 W hacia el vacío de fondo.
Disco trasero (negro):
| > |
Q2i1='Q1i2';Q2i1_:=Q1i2_;Q2i3:=A2*F23*(M2-M3);Q2i3_:=subs(sol_,A2=A_,F23=F13_,M3=0,dat,SI0,%)*W_;Q2e:=epsilon2*A2*M2bb;Q2e_:=subs(sol_,A2=A_,M3=0,dat,SI0,%)*W_; |
i.e. los Q21=60 W netos que absorbe el disco 2 del disco 1, los evacúa al vacío de fondo: 49 W hacia atrás, y los restantes 11 W hacia delante (por la corona que deja libre el disco 1).
NOTA. El telescopio James Webb, JWST, que irá alrededor de SEL2, usa un escudo parasol formado por 5 capas de unos 21×14 m2 de superficie, separadas unos 0,2 m entre sí, y hechas de kapton de 25 m excepto la capa que mira al sol que es de 50 m. Las cinco capas de kapton están metalizadas con 100 nm de aluminio (baja emisividad), y las dos primeras tienen un revestimiento de 50 nm de silicio dopado de alta emisividad. La alta reflectancia del aluminio ayuda a evacuar parte de la radiación infrarroja al espacio por los huecos laterales. Las capas son de tamaño y forma ligeramente diferentes. La capa 5 (próxima al espejo primario) es la más pequeña; la capa 1 (expuesta al sol) es relativamente plana y la capa 5 es más curva (cóncava hacia el telescopio); las capas están más juntas en el centro y más separadas en los bordes para dirigir el calor desde el centro hacia el exterior.
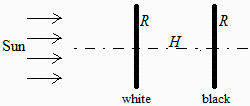
![Typesetting:-mprintslash([T1 := `+`(`*`(`/`(1, 2), `*`(`^`(2, `/`(3, 4)), `*`(`^`(`/`(`*`(alpha1, `*`(EL2)), `*`(epsilon1, `*`(sigma))), `/`(1, 4))))))], [`+`(`*`(`/`(1, 2), `*`(`^`(2, `/`(3, 4)), `*`...](images/p74_9.gif)

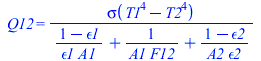
![Typesetting:-mprintslash([Q12 := `/`(`*`(A, `*`(`+`(M1bb, `-`(M2bb)))), `*`(`+`(`/`(1, `*`(epsilon1)), `/`(1, `*`(epsilon2)), `-`(1))))], [`/`(`*`(A, `*`(`+`(M1bb, `-`(M2bb)))), `*`(`+`(`/`(1, `*`(eps...](images/p74_19.gif)
