| > | restart:#"m13_p70" |
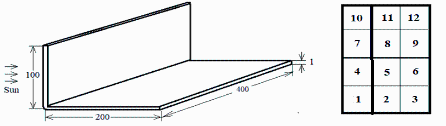
Este ejercicio es continuación del problema resuelto en m11_p92 (“Se quiere estudiar el campo de temperaturas en un apéndice de un satélite geoestacionario, cuyo modelo simplificado puede aproximarse por una placa de aluminio A7075 de LxLyLz=300×400×1 mm3 doblada en ángulo recto a 1/3 de Lx y expuesta al sol por la cara menor como se muestra en la figura.”).
Se quiere ahora resolver el caso de 12 nodos indicado en la figura, i.e. calcular las 12 temperaturas representativas de los 12 trozos de chapa. Para ello se pide:
a) Calcular todos los factores de vista entre los 12 parches usando la expresión ‘Perpendicular configurations/ Rectangle to rectangle’ de la Tabla.
b) Calcular el factor de vista desde la superficie 1 hasta el conjunto 2+3+5+6 y hasta toda la placa vista.
c) Como comprobación, calcular el factor de vista entre el conjunto 1+4 y el conjunto 2+3+5+6, como combinación de los anteriores, y con la expresión ‘Perpendicular configurations / Square plate to rectangular plate’ de la Tabla.
d) Plantear todas las ecuaciones nodales.
e) Obtener las temperaturas en régimen estacionario con sol frontal.
f) Calcular los coeficientes h en la expresión para cada parche, y comparar con la expresión dada en el apartado f de m11_p92.

Fig. 1. Dimensiones de la placa doblada, y numeración de los 12 trozos de 100·100 mm2 considerados (1, 4, 7 y 10 están en el tramo vertical, iluminado).
| > | with(RealDomain):read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):assume(h_>0,r>0):unprotect(D):with(plots): |
| > | su:="Al-7075":dat:=[L=0.1*m_,A=0.01*m_^2,Ac=100e-6*m_,C=27*J_/K_,Lx=0.3*m_,Ly=0.4*m_,Lz=1e-3*m_,Lxh=0.2*m_,Lxv=0.1*m_,E=1360*W_/m_^2,Tinf=2.7*K_,her=1*W_/(m_^2*K_),alpha=1,epsilon=1];datS:=get_sol_data(su);dat:=op(dat),datS,Const,SI2,SI1: |
a) Calcular todos los factores de vista entre los 12 parches usando la expresión ‘Perpendicular configurations/ Rectangle to rectangle’ de la Tabla.
En todo el problema haremos uso de que todas las áreas de los parches son iguales: las de la cara, A=0,1·0,1=0,01 m2, y las de contacto, Ac=0,1·0,001=0,0001 m2.
Vemos también que, como hay un plano de simetría, basta resolver la mitad de los parches (1,2,3,4,5,6).
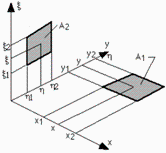
Tabla. Desde el rectángulo (x1,x2,y1,y2) hacia el rectángulo (xi1,xi2,eta1,eta2):
| > | F12:=S4/(2*Pi*A1);A1:=((x[2]-x[1])*(y[2]-y[1]));B:=((y-eta)*C*arctan(D)-(1/4)*C^2*(1-D^2)*ln(C^2*(1+D^2)));D:=(y-eta)/C;C:=sqrt(x^2+xi^2);S4:=sum(sum(sum(sum((-1)^(i+j+k+l)*subs(x=x[i],y=y[j],eta=eta[k],xi=xi[l],B),i=1..2),j=1..2),k=1..2),l=1..2): |
Desde el parche 1 hasta lcada uno de los 8 vistos: (tomaremos 4 decimales por la dificultad de este lenguaje de programación para imponer un número de cifras significativas):
| > | dat1:=[seq([x[1]=1e-6,x[2]=1,xi[1]=0,xi[2]=1,y[1]=0,y[2]=1,eta[1]=0+i,eta[2]=1+i],i=0..3),seq([x[1]=1e-6,x[2]=1,xi[1]=1,xi[2]=2,y[1]=0,y[2]=1,eta[1]=0+i,eta[2]=1+i],i=0..3)]:eqF1_to_2_5_8_11_3_6_9_12:=seq(evalf(subs(dat1[i],value(F12))),i=1..8);F1_to_inf:=1-convert([%],`+`); |
Desde el parche 4 hasta lcada uno de los 8 vistos:
| > | dat4:=[seq([x[1]=1e-6,x[2]=1,xi[1]=0,xi[2]=1,y[1]=1,y[2]=2,eta[1]=0+i,eta[2]=1+i],i=0..3),seq([x[1]=1e-6,x[2]=1,xi[1]=1,xi[2]=2,y[1]=1,y[2]=2,eta[1]=0+i,eta[2]=1+i],i=0..3)]:eqF4_to_2_5_8_11_3_6_9_12:=seq(evalf(subs(dat4[i],value(F12))),i=1..8);F1_to_inf:=1-convert([%],`+`); |
Poniéndolos todos ordenados, i.e. de 1 a 1,2,3,4,5,6,7,8,9,10,11,12,inf
| > | F1j:=[0,0.2000,0.0328,0,0.0406,0.0189,0,0.0043,0.0059,0,0.0009,0.0019,0.6946];F4j:=[0,0.0406,0.0189,0,0.2000,0.0328,0,0.0406,0.0189,0,0.0043,0.0059,0.6379]; |
Las relaciones de reciprocidad y simetría:
| > | eqF_:=F[2,1]=F[1,2],F[2,4]=F[4,2],F[2,7]=F[4,11],F[2,10]=F[1,11], F[3,1]=F[1,3],F[3,10]=F[1,12],F[3,4]=F[4,3],F[3,7]=F[4,12], F[5,1]=F[1,5],F[5,4]=F[4,5],F[5,7]=F[4,8],F[5,10]=F[1,8], F[6,1]=F[1,6],F[6,4]=F[4,6],F[6,10]=F[1,9],F[6,7]=F[4,9];eqF:=F[1,2]=F1j[2],F[1,3]=F1j[3],F[1,5]=F1j[5],F[1,6]=F1j[6],F[1,8]=F1j[8],F[1,9]=F1j[9],F[1,11]=F1j[11],F[1,12]=F1j[12],F[1,inf]=F1j[13],F[4,2]=F4j[2],F[4,3]=F4j[3],F[4,5]=F4j[5],F[4,6]=F4j[6],F[4,8]=F4j[8],F[4,9]=F4j[9],F[4,11]=F4j[11],F[4,12]=F4j[12],F[4,inf]=F4j[13];eqT_:=T7=T4,T8=T5,T9=T6,T10=T1,T11=T2,T12=T3; |
b) Calcular el factor de vista desde la superficie 1 hasta el conjunto 2+3+5+6 y hasta toda la placa vista.
De 1 a 2+3+5+6 sera la suma, y de 1 a toda la placa será la suma total, que ya la hemos usado antes para calcular F1,inf.
| > | F[1,2356]:=F[1,2]+F[1,3]+F[1,5]+F[1,6];'F[1,2356]'=subs(eqF_,eqF,%);F[1,23456789101112]:=F[1,2]+F[1,3]+F[1,5]+F[1,6]+F[1,8]+F[1,9]+F[1,11]+F[1,12];'F[1,23456789101112]'=subs(eqF_,eqF,%);'F[1,inf]'=1-rhs(%); |
i.e. de 1 a 2 era F[1,2]=0,2, de 1 a 2+3+5+6 aumenta a F[1,2356]=0,29, y de 1 a toda la placa apenas aumenta a F[1,23456789101112]=0,31 (el resto va al espacio, F[1,inf])=0,69).
c) Como comprobación, calcular el factor de vista entre el conjunto 1+4 y el conjunto 2+3+5+6, como combinación de los anteriores, y con la expresión ‘Perpendicular configurations / Square plate to rectangular plate’ de la Tabla.
Con los datos anteriores y el álgebra de los facores de vista:
| > | eq_distr:=F[i,jk]=F[i,j]+F[i,k];eq_comp:=F[ij,k]=(Ai*F[i,k]+Aj*F[j,k])/(Ai+Aj);eq_distr14:=F[14,2356]=F[14,2]+F[14,3]+F[14,5]+F[14,6];eq_comp14:=F[14,2]=(F[1,2]+F[4,2])/2;eq_distr_comp14:=F[14,2356]=(1/2)*(F[1,2]+F[4,2]+F[1,3]+F[4,3]+F[1,5]+F[4,5]+F[1,6]+F[4,6]);eq_distr_comp14_:=subs(eqF,eq_distr_comp14);####eq_distr_comp14_:=F[14,2356]=(1/2)*(F1j[2]+F1j[3]+F1j[5]+F1j[6]+F4j[2]+F4j[3]+F4j[5]+F4j[6]); |
mientras que directamente:
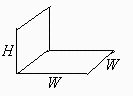
| > | F12:=1/4+(1/Pi)*(h*arctan(1/h)-h1*arctan(1/h1)-(h^2/4)*ln(h2));h2:=h1^4/(h^2*(h^2+2));h1:=sqrt(1+h^2);eqh:=h=H/W;eqh:=h=1/2;eq_distr_comp14__:=F[14,2356]=2*F12;eq_distr_comp14__:=evalf(subs(eqh,%)); |
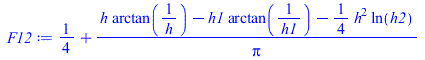 |
![F[14, 2356] = `+`(`/`(1, 2), `/`(`*`(2, `*`(`+`(`*`(h, `*`(arctan(`/`(1, `*`(h))))), `-`(`*`(`^`(`+`(`*`(`^`(h, 2)), 1), `/`(1, 2)), `*`(arctan(`/`(1, `*`(`^`(`+`(`*`(`^`(h, 2)), 1), `/`(1, 2)))))))),...](images/p70_39.gif) |
que coinciden.
d) Plantear todas las ecuaciones nodales.
Los 12 nodos tienen la misma capacidad térmica, pero cada uno tienes sus acoplamientos conductivos y radiativos. Por simetría, basta establecer las 6 ecuaciones nodales 1-2-3-4-5-6.
Suponiendo superficies negras, y despreciando 2,7 K frente a las Ts esperadas:
Nodo 1:
| > | C:='C':eq:=C*dT/dt=Wdis+Q;eq:=C*dT/dt=alpha*E*A+Qcond+Qrad;eqC:=C=m*c;eqC:=C=rho*A*Lz*c;eqC_:=subs(datS,dat,%);eq1:=C*dT1/dt=alpha*E*A+Qcond12+Qcond14+Qrad12+Qrad13+Qrad15+Qrad16+Qrad18+Qrad19+Qrad111+Qrad112+Qrad1inf+Qrad1inf_; |
donde Qrad1inf_ corresponde a la emisión por la cara opuesta (la convexa). Desarrollando:
| > | eq1:=C*dT1/dt=alpha*E*A+k*Ac*(T2-T1)/L+k*Ac*(T4-T1)/L+AF[1,2]*sigma*(T2^4-T1^4)+AF[1,3]*sigma*(T3^4-T1^4)+AF[1,5]*sigma*(T5^4-T1^4)+AF[1,6]*sigma*(T6^4-T1^4)+AF[1,8]*sigma*(T8^4-T1^4)+AF[1,9]*sigma*(T9^4-T1^4)+AF[1,11]*sigma*(T11^4-T1^4)+AF[1,12]*sigma*(T12^4-T1^4)+AF[1,inf]*sigma*(Tinf^4-T1^4)+A*sigma*(Tinf^4-T1^4);eq1:=C*dT1/dt=alpha*E*A+k*Ac*(T2-T1)/L+k*Ac*(T4-T1)/L+sigma*A*(F[1,2]*T2^4+F[1,3]*T3^4+F[1,5]*T5^4+F[1,6]*T6^4+F[1,8]*T8^4+F[1,9]*T9^4+F[1,11]*T11^4+F[1,12]*T12^4-2*T1^4);eq1_:=subs(eqT_,eqF_,eqF,dat,SI0,%); |
Nodo 4 (Nótese que Qcond47=0 por simetría):
| > | eq4:=C*dT4/dt=alpha*E*A+k*Ac*(T1-T4)/L+k*Ac*(T5-T4)/L+sigma*A*(F[4,2]*T2^4+F[4,3]*T3^4+F[4,5]*T5^4+F[4,6]*T6^4+F[4,8]*T8^4+F[4,9]*T9^4+F[4,11]*T11^4+F[4,12]*T12^4-2*T4^4);eq4_:=subs(eqT_,eqF_,eqF,dat,SI0,%); |
Nodo 2:
| > | eq2:=C*dT2/dt=k*Ac*(T1-T2)/L+k*Ac*(T5-T2)/L+k*Ac*(T3-T2)/L+sigma*A*(F[2,1]*T1^4+F[2,4]*T4^4+F[2,7]*T7^4+F[2,10]*T10^4-2*T2^4);eq2_:=subs(eqT_,eqF_,eqF,dat,SI0,%); |
Nodo 3:
| > | eq3:=C*dT3/dt=k*Ac*(T2-T3)/L+k*Ac*(T6-T3)/L+sigma*A*(F[3,1]*T1^4+F[3,4]*T4^4+F[3,7]*T7^4+F[3,10]*T10^4-2*T3^4);eq3_:=subs(eqT_,eqF_,eqF,dat,SI0,%); |
Nodo 5:
| > | eq5:=C*dT5/dt=k*Ac*(T2-T5)/L+k*Ac*(T4-T5)/L+k*Ac*(T6-T5)/L+sigma*A*(F[5,1]*T1^4+F[5,4]*T4^4+F[5,7]*T7^4+F[5,10]*T10^4-2*T5^4);eq5_:=subs(eqT_,eqF_,eqF,dat,SI0,%); |
Nodo 6:
| > | eq6:=C*dT6/dt=k*Ac*(T5-T6)/L+k*Ac*(T3-T6)/L+sigma*A*(F[6,1]*T1^4+F[6,4]*T4^4+F[6,7]*T7^4+F[6,10]*T10^4-2*T6^4);eq6_:=subs(eqT_,eqF_,eqF,dat,SI0,%); |
e) Obtener las temperaturas en régimen estacionario con sol frontal.
| > | r:=10..400:sol_:=fsolve(subs(dT1=0,dT2=0,dT3=0,dT4=0,dT5=0,dT6=0,{eq1_,eq2_,eq3_,eq4_,eq5_,eq6_}),{T1,T2,T3,T4,T5,T6},{T1=r,T2=r,T3=r,T4=r,T5=r,T6=r});'T1'=TKC(subs(sol_,T1*K_));'T2'=TKC(subs(sol_,T2*K_));'T3'=TKC(subs(sol_,T3*K_));'T4'=TKC(subs(sol_,T4*K_));'T5'=TKC(subs(sol_,T5*K_));'T6'=TKC(subs(sol_,T6*K_)); |
i.e. volvemos a ver que transversalmente a la dirección del Sol apenas varía la temperatura (e.g. T1=19,3 ºC, T4=19,7 ºC, T7=T4=19,7 ºC, T10=T1=19,3 ºC), y que la caída de temperatura es mucho mayor desde la franja iluminada (T14710=19,5 ºC hasta la 1ª franja (T25811=-25 ºC, i.e. un salto de 19-(-25)=44 ºC), que hasta la 2ª franja (T36912=-45 ºC, i.e. un salto de -25-(-45)=20 ºC).
f) Calcular los coeficientes h en la expresión para cada parche, y comparar con la expresión dada en el apartado f de m11_p92.
| > | eqh:=Qrad=-h*A*(T-Tinf);eqh1:=-(Qrad12+Qrad13+Qrad15+Qrad16+Qrad18+Qrad19+Qrad111+Qrad112+Qrad1inf+Qrad1inf_)/(A*T1);eqh1:=-(sigma*(F[1,2]*T2^4+F[1,3]*T3^4+F[1,5]*T5^4+F[1,6]*T6^4+F[1,8]*T8^4+F[1,9]*T9^4+F[1,11]*T11^4+F[1,12]*T12^4-2*T1^4))/T1;eqh1_:=subs(eqT_,eqF_,eqF,sol_,dat,SI0,%);eqh2:=-(sigma*(F[2,1]*T1^4+F[2,4]*T4^4+F[2,7]*T7^4+F[2,10]*T10^4-2*T2^4))/T2;eqh2_:=subs(eqT_,eqF_,eqF,sol_,dat,SI0,%);eqh3:=-(sigma*(F[3,1]*T1^4+F[3,4]*T4^4+F[3,7]*T7^4+F[3,10]*T10^4-2*T3^4))/T3;eqh3_:=subs(eqT_,eqF_,eqF,sol_,dat,SI0,%);eqh4:=-(sigma*(F[4,2]*T2^4+F[4,3]*T3^4+F[4,5]*T5^4+F[4,6]*T6^4+F[4,8]*T8^4+F[4,9]*T9^4+F[4,11]*T11^4+F[4,12]*T12^4-2*T4^4))/T4;eqh4_:=subs(eqT_,eqF_,eqF,sol_,dat,SI0,%);eqh5:=-(sigma*(F[5,1]*T1^4+F[5,4]*T4^4+F[5,7]*T7^4+F[5,10]*T10^4-2*T5^4))/T5;eqh5_:=subs(eqT_,eqF_,eqF,sol_,dat,SI0,%);eqh6:=-(sigma*(F[6,1]*T1^4+F[6,4]*T4^4+F[6,7]*T7^4+F[6,10]*T10^4-2*T6^4))/T6;eqh6_:=subs(eqT_,eqF_,eqF,sol_,dat,SI0,%); |
La comparación con la expresión dada en el apartado f de m11_p92 puede considerarse aceptable, aunque allí la media era de 1,2 W/(m2·K) y aquí sería de casi 2 W/(m2·K). Donde más se devía es en el valor máximo, que no se da en el extremo fría sino en el más caliente, como era de esperar al tratarse de una linealización de las pérdidas radiativas, que aumentan mucho con la temperatura (h=4·sigma·Tmean^3).
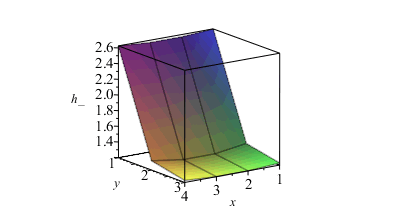
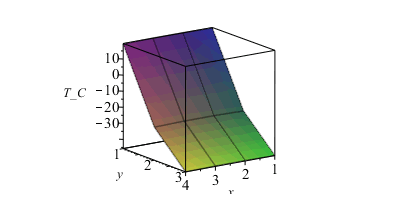
Podemos representar estos valores en forma matricial (y también las temperaturas):
| > | h_:=Matrix(4,3,[eqh1_,eqh2_,eqh3_,eqh4_,eqh5_,eqh6_,eqh4_,eqh5_,eqh6_,eqh1_,eqh2_,eqh3_]);matrixplot(h_,labels=[x,y,'h_']);T_K:=Matrix(4,3,subs(sol_,[T1,T2,T3,T4,T5,T6,T4,T5,T6,T1,T2,T3])):To:=Matrix(4,3,273.15):T_C:=T_K-To;matrixplot(T_C,labels=[x,y,'T_C']); |
 |
 |
 |
 |
| > |