| > | restart:#"m13_p69" |
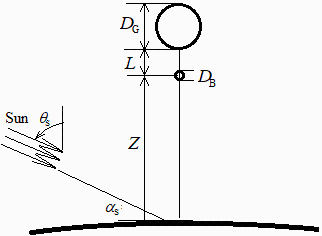
Consid├®rese un globo estratosf├®rico de 130 m de di├Īmetro a 40 km de altitud sobre la base de McMurdo en Ant├Īrtica (latitud ’ü”=’ĆŁ77,8┬║), en el solsticio iluminado. Del globo cuelga una barquilla de 2 m de di├Īmetro a 60 m del globo. Suponiendo despreciable el efecto del aire (a esa altitud es p<0,3 kPa), que el globo es blanco y la barquilla negra, se pide:
a) Calcular los factores de vista desde el globo a tierra, y desde la barquilla al globo y a tierra, as├Ł como la elevaci├│n del sol sobre el horizonte a mediod├Ła y a medianoche, despreciando el efecto de las nubes.
b) Plantear el balance t├®rmico estacionario del globo considerado isotermo, calculando las cargas t├®rmicas suponiendo que en la Ant├Īrtida el albedo es ’ü▓s=0,9 y la emisi├│n infrarroja terrestre por encima de la atm├│sfera es M=160 W/m2.
c) Calcular la temperatura del globo.
d) Plantear el balance t├®rmico estacionario de la barquilla considerada isoterma.
e) Calcular la temperatura de la barquilla.
Datos:
| > | read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):with(plots): |
| > | dat:=[D=130*m_,Z=40e3*m_,phi=-77.8*Pi/180,d=2*m_,L=60*m_,delta=-23.55*Pi/180,E=1407*W_/m_^2,alpha=0.2,epsilon=0.8,Tinf=2.7*K_,rho[T]=0.9,M=160*W_/m_^2];dat:=op(dat),Const,SI2,SI1: |
El solsticio en que la Ant├Īrtida est├Ī iluminada de d├Ła y de noche es el solsticio sur o solsticio de diciembre (cerca del 21 de diciembre de cada a├▒o), que en Europa llamamos solsticio de invierno (nuestro).
Tomaremos para el globo blanco alpha=0.2, epsilon=0.8, aunque en realidad estos globos son semitransparentes y, aunque la absortancia solar global s├Ł que se aproxima a alpha=0,2, la reflectancia no es la de cuerpo opaco (rho=1-alpha=1-0,2=0,8) sino mucho menor (rho=0,25 o as├Ł). La emisividad global tambi├®n es algo menor (unos 0,6 en vez de 0,8). La irradiancia solar es la de enero, E=E0┬Ę(1+e)^2=1361┬Ę(1+0,0167)^2=1407 W/m2.
Cuidado que vamos a usar G=Globo y B=Barquilla, pero se podr├Ła haber usado B=Balloon y G=Gondola.
a) Calcular los factores de vista desde el globo a tierra, y desde la barquilla al globo y a tierra, as├Ł como la elevaci├│n del sol a mediod├Ła y a medianoche, despreciando el efecto de las nubes.
Si la Tierra fuese plana e infinita ser├Ła F12=1/2. Desde una esfera hacia otra mucho mayor es F12=(1-sqrt(1-1/h^2))/2, por lo que, desde el globo a la tierra (tomanodo R=6370 km, sin nubes) es:
| > | eqF12:=F[12]=(1-sqrt(1-1/h^2))/2;eqh:=h=(Z+R[T])/R[T]; eqhGT:=subs(dat,%);eqF12GT:=subs(eqhGT,eqF12); |
![Typesetting:-mprintslash([eqF12 := F[12] = `+`(`/`(1, 2), `-`(`*`(`/`(1, 2), `*`(`^`(`+`(1, `-`(`/`(1, `*`(`^`(h, 2))))), `/`(1, 2))))))], [F[12] = `+`(`/`(1, 2), `-`(`*`(`/`(1, 2), `*`(`^`(`+`(1, `-`...](images/p691_3.gif) |
|
| (1) |
i.e. el 44% de lo que emite el globo va a la tierra (y el 56% restante al cielo). Desde la barquilla al globo y a la tierra:
| > | eqhBT:=subs(dat,eqh);eqF12BT:=subs(eqhGT,eqF12);eqh:=h=(L+R[G])/R[G];eqRG:=R[G]=D/2;eqRG_:=subs(dat,%);eqhGT:=evalf(subs(%,dat,eqh));eqF12BG:=subs(eqhGT,eqF12); |
| (2) |
i.e. el 44% de lo que emite la barquilla va a tierra, y solo el 7,3% al globo (el 49% restante va al cielo).
Elevaci├│n solar a mediod├Ła y a medianoche. En el solsticio iluminado la declinaci├│n solar es delta=-23,5┬║ y las elevaciones solares:
| > | eqNoon:=alpha[s]=Pi/2-abs(phi-delta);eqNoon_:=alpha[s]=evalf(subs(dat,rhs(%)));alpha[s]=evalf(rhs(%)*180/Pi)*'┬║';eqMidnight:=alpha[s]=abs(-phi-delta)-Pi/2;eqMidnight_:=alpha[s]=evalf(subs(dat,rhs(%)));alpha[s]=evalf(rhs(%)*180/Pi)*'┬║'; |
| (3) |
i.e. a mediod├Ła el sol est├Ī a 35.8┬║ por encima del horizonte, y a medianoche a 11.4┬║.
b) Plantear el balance t├®rmico estacionario del globo considerado isotermo, calculando las cargas t├®rmicas suponiendo que en la Ant├Īrtida el albedo es ’ü▓s=0,9 y la emisi├│n infrarroja terrestre por encima de la atm├│sfera es M=160 W/m2.
Suponer el globo isotermo parece muy dr├Īstico (d├Īndole el sol por un lado): la conducci├│n por la delgada capa s├│lida ser├Ī despreciable, y la convecci├│n natural del gas interior (helio) y del aire exterior no ser├Īn muy efectivas; la mayor uniformizaci├│n ser├Ī por radiaci├│n infrarroja por el interior.
Aunque no es un cuerpo negro, al ser la tierra tan grande y el espacio de fondo tan fr├Ło, quedan desacoplados y el balance t├®rmico (la barquilla apenas cuenta) es:
| > | eqBE:=m*c*dT/dt=Qs+Qa+Qp-Qinf;eqQs:=Qs=alpha*E*A/4;eqA:=A=Pi*D^2;eqA_:=evalf(subs(dat,%));eqQs_:=subs(eqA,dat,eqQs); |
| (4) |
i.e. el globo absorbe del sol directamente 3,7 MW en todo momento. Para el sol reflejado hay que tener en cuenta la irradiancia horizontal, que var├Ła con la altura solar.
Para la entrada por albedo vamos a considerar que el casquete visible desde el globo est├Ī uniformemente iluminado por el sol (e.g. con una elevaci├│n de 35,5┬║ a mediod├Ła, pese a que en la zona del casquete m├Īs pr├│xima al sol ser├Ła 35,5+6,4=41,9┬║ y en la zona m├Īs alejada 35,5-6,4=29,1┬║, y las reflexiones ser├Łan en ellos de sin41,9=0,67 y sin29,1=0,49, en vez de sin35,5=0,58 aplicado a toda el ├Īrea; no hay que olvidar que, debido a los factores de vista, la zona que m├Īs influye es la tierra m├Īs pr├│xima).
Para ver el tama├▒o del casquete, sea theta[H] el semi-├Īngulo:
| > | eqCap:=theta[H]=arccos(R[T]/(R[T]+Z));eqCap_:=evalf(subs(dat,%));evalf(rhs(%)*180/Pi)*'┬║';Rc:=theta[H]*R[T];Rc_:=evalf(subs(eqCap_,dat,%)); |
| (5) |
i.e. la tangente a la tierra desde el globo est├Ī 6,4┬║ por debajo del plano horizontal, a una distancia esf├®rica de 712 km (712┬Ęcos6,4┬║=708 km en proyecci├│n plana). Considerando plano ese casquete, la radiaci├│n solar reflejada que absorbe el globo ser├Ła:
| > | eqQa:=Qa=alpha*A*F[12]*E*sin(alpha[s])*rho[T];eqQa_Noon:=subs(dat,evalf(subs(eqNoon,eqF12GT,eqA,dat,eqQa)));eqQa_Midn:=subs(dat,evalf(subs(eqMidnight,eqF12GT,eqA,dat,eqQa))); |
| (6) |
i.e. de albedo absorbe 3,5 MW a mediod├Ła y 1,2 MW a medianoche..
La absorci├│n de la emisi├│n infrarroja planetaria es:
| > | eqQp:=Qp=epsilon*A*F[12]*M;eqQp_:=subs(eqF12GT,eqA,dat,eqQp) |
| (7) |
i.e. se absorben 3 MW de IR.
c) Calcular la temperatura del globo.
Como toda esa energ├Ła ha de emitirse en el IR por toda el ├Īrea del globo (tambi├®n la que apunta a la tierra), la temperatura estacionaria, despreciando la Tinf^4, ser├Ła:
| > | eqQinf:=epsilon*A*sigma*T[G]^4;'Qinf=Qs+Qa+Qp';eqTG:=T[G]=sqrt(sqrt(('Qs+Qa+Qp')/(epsilon*A*sigma)));TG_Noon:=evalf(subs(eqA,eqQs_,eqQa_Noon,eqQp_,dat,SI0,rhs(eqTG)))*K_;'TG_Noon'=TKC(%);TG_Midn:=evalf(subs(eqA,eqQs_,eqQa_Midn,eqQp_,dat,SI0,rhs(eqTG)))*K_;'TG_Midn'=TKC(%); |
| (8) |
i.e. el globo quedar├Ła a -18 ┬║C a mediod├Ła, y a -34 ┬║C a medianoche. En realidad, en este tipo de globos suele haber una diferencia de hasta 50 ┬║C entre la zona que apunta al sol y la opuesta.
d) Plantear el balance t├®rmico estacionario de la barquilla considerada isoterma.
Ahora, adem├Īs de las cargas terrestres en ambas bandas (Qa y Qp) hay qua a├▒adir las cargas debidas al globo en ambas bandas (QaG y Qg). Los correspondientes Qs, Qa, y Qp para la barquilla, considerada como cuerpo negro, son:
| > | eqBE:=m*c*dT/dt=Qs+Qa+QaG+Qp+Qg-Qinf;eqQs:=Qs=E*Ab/4;eqAb:=Ab=Pi*d^2;eqAb_:=evalf(subs(dat,%));eqQs_:=evalf(subs(eqAb,dat,eqQs));eqQa:=Qa=Ab*F[GT]*rho[T]*E*sin(alpha[s]);eqQa_Noon:=subs(dat,evalf(subs(eqNoon_,F[GT]=rhs(eqF12GT),eqAb,dat,eqQa)));eqQa_Midn:=subs(dat,evalf(subs(eqMidnight_,F[GT]=rhs(eqF12GT),eqAb,dat,eqQa)));eqQp:=Qp=Ab*F[GT]*M;eqQp_:=subs(dat,evalf(subs(F[GT]=rhs(eqF12GT),eqAb,dat,eqQp))); |
| (9) |
i.e. la barquilla esf├®rica de 2 m de di├Īmetro absorbe 4,4 kW del sol directo, 4,1 kW del albedo terrestre a mediod├Ła (1,4 kW a medianoche), y 0,9 kW de infrarrojo terrestre.
Adem├Īs recibe las cargas t├®rmicas del globo (albedo m├Īs IR). La de IR con el modelo isotermo es f├Īcil de calcular sabiendo la temperatura del globo:
| > | eqQg:=Qg=epsilon*Ab*F[BG]*sigma*'TG'^4;eqQg_Noon:=subs(TG=TG_Noon,F[BG]=rhs(eqF12BG),eqAb,dat,eqQg);eqQg_Midnight:=subs(TG=TG_Midn,F[BG]=rhs(eqF12BG),eqAb,dat,eqQg); |
| (10) |
i.e. del globo recibe en el IR 176 W a mediod├Ła y 137 W a medianoche. Pero lo que recibe por reflexi├│n solar en el globo es muy complicado porque el modelo de irradiancia solar uniforme no es bueno, y porque adem├Īs habr├Ła que tener en cuenta la doble reflexi├│n solar que le llegar├Ła de la tierra.
Sea theta[G] el semi-├Īngulo con el que se ve el globo desde la barquilla::
| > | eqcap:=theta[G]=arcsin(R[G]/(L+R[G]));eqcap_:=evalf(subs(eqRG,dat,%));'theta[G]'=evalf(rhs(%)*180/Pi)*'┬║';'alpha[G]'=evalf((Pi/2-rhs(eqcap_))*180/Pi)*'┬║'; |
| (11) |
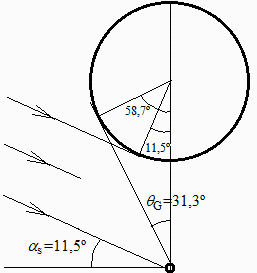
i.e. desde la barquilla el globo abarca un semi├Īngulo de 31,3┬║, lo que significa que tapa el cielo desde una elevaci├│n de 58,7┬║ desde el plano horizontal que pasa por la barquilla. Como la elevaci├│n m├Īxima del sol en McMurdo es de 35,8┬║, el globo nunca le tapa el sol a la barquilla.
La reflexi├│n solar directa en el globo que llega a la barquilla no ser├Ī muy grande porque el sol incide por arriba. El m├Īximo ser├Ła a medianoche, con el sol s├│lo 11,4┬║ por encima del plano horizontal, por lo que desde la barquilla solo se ver├Ła iluminada por el sol una parte de globo en forma de luna, correspondiente a ├Īngulos centrados en el globo desde 11,4┬║ hasta 58,7┬║, como se muestra en la figura. Luego estimaremos su valor.
La reflexi├│n solar indirecta ser├Ī mayor debido a las grandes reflectancias de la tierra rho[T]=0,9 y del globo, rho[G]=1-alpha=1-0,2=0,8. El valor m├Īximo de esta re-reflectancia ser├Ī a mediod├Ła:
| > | eqMrere:=Mrr=E*sin(alpha[s])*rho[T]*(1-alpha);eqMrereNoon_:=subs(dat,evalf(subs(eqNoon_,dat,%)));eqMrereMidnight_:=subs(dat,evalf(subs(eqMidnight_,dat,eqMrere))); |
| (12) |
i.e. de los E=1400 W/m2 de irradiancia normal en el solsticio, sobre una superficie horizontal a mediod├Ła solo llegan E┬Ęsin(alpha)=823 W/m2 a la tierra, reflej├Īndose 740 W/m2 hacia arriba de forma difusa, que llegan a la parte baja del globo (a un plana horizontal a 40 km de altitud con el modelo de tierra plana), del cual se reflejan 592 W/m2 hacia abajo. Suponiendo que toda el ├Īrea del globo visible desde la barquilla reflejase lo mismo (reflejar├Ī menos porque llega menos a las zonas laterales), la absorci├│n en la barquilla ser├Ła:
| > | eqQaGind:=QaGind=Ab*F[BG]*Mrr;eqQaGindNoon_:=subs(F[BG]=F[12],eqF12BG,eqAb,eqMrereNoon_,dat,%);eqQaGindMidnight_:=subs(F[BG]=F[12],eqF12BG,eqAb,eqMrereMidnight_,dat,eqQaGind); |
| (13) |
que vemos que son bastante menores que la carga por albedo terrestre (4,1 kW) pero mayores que el IR del globo (177 W).
La reflexi├│n solar directa en el globo es m├Īs dif├Łcil de estimar. Desde la barquilla, el lado iluminado del globo se ve como una luna (mayor a medianoche por estar m├Īs bajo el sol). Con la siguiente aproximaci├│n ser├Ła:
| > | eqQaGdir:=QaGdir=Ab*F[BG]*rho[G]*E*((1+cos(phi))/2)^2*(1-(phi/phiee)^2); |
| (14) |
estando los ├Īngulos ahora referidos a la direcci├│n solar, y siendo phi=90+11,5=101,5┬║ y el phi de entrada en eclipse (si el globo fuese un planeta y la barquilla un sat├®lite) ser├Ła phiee=Pi-arcsin(RG/(RG+L))=Pi-arcsin(65/125)=149┬║. Por tanto:
| > | eqQaGdirMidnight_:=subs(dat,evalf(subs(phi=101.5,phiee=149,eqAb_,F[BG]=rhs(eqF12BG),rho[G]=1-alpha,dat,eqQaGdir)));eqQaGdirNoon_:=subs(dat,evalf(subs(phi=125.7,phiee=149,eqAb_,F[BG]=rhs(eqF12BG),rho[G]=1-alpha,dat,eqQaGdir))); |
| (15) |
i.e. la barquilla recibe por reflexi├│n solar directa en el globo 324 W a mediod├Ła y 370 W a medianoche.
En resumen:
| > | QaG_Noon_:=rhs(eqQaGindNoon_)+rhs(eqQaGdirNoon_);QaG_Midnight_:=rhs(eqQaGindMidnight_)+rhs(eqQaGdirMidnight_); |
| (16) |
e) Calcular la temperatura de la barquilla.
| > | eqBE;eqQinf:=epsilon*Ab*sigma*T[B]^4;'Qinf=Qs+Qa+Qp+QaG+Qg';eqTB:=T[B]=sqrt(sqrt(('Qs+Qa+Qp+QaG+Qg')/(Ab*sigma)));TB_Noon:=evalf(subs(eqAb,eqQs_,eqQa_Noon,eqQp_,eqQg_Noon,QaG=QaG_Noon_,eqAb,dat,SI0,rhs(eqTB)))*K_;'TB_Noon'=TKC(%);TB_Midn:=evalf(subs(eqA,eqQs_,eqQa_Midn,eqQp_,eqQg_Midnight,QaG=QaG_Midnight_,eqAb,dat,SI0,rhs(eqTB)))*K_;'TB_Midn'=TKC(%); |
| (17) |
i.e. la barquilla quedar├Ła a 75 ┬║C a mediod├Ła, y a 46 ┬║C a medianoche, en ambos casos mucho m├Īs caliente (por ser negra) que el globo (que es blanco). En la realidad, estos globos son de una delgada capa de polietileno (o varias); tan delgada que es dejan pasar m├Īs del 50% de las radiaciones solares e infrarrojas (tambi├®n son un poco permeables al helio y dem├Īs gases, lo que limita su vida).
Pueden verse m├Īs detalles de un caso similar para un globo ├Īrtico.
| > |