| > | restart:#"m13_p68" |
Para un análisis térmico de un apéndice en un satélite geoestacionario, se quiere estudiar el intercambio radiativo entre dos bandas semicilíndricas delgadas, paralelas y coaxiales, de relación de radios R2/R1=2 e igual longitud L>>R2, estando la mayor (2) con su cara convexa (externa, 2e) apuntando al Sol, y la menor (1) con su cara convexa (externa, 1e) apuntando en dirección opuesta. Para el caso en que todas las superficies radien idealmente y sea R1=20 mm, se pide:
a) Factor de vista desde la cara interior de la banda 1 (1i) hacia la banda 2, por razonamiento deductivo basado en el álgebra de los factores de vista.
b) Factor de vista desde la cara exterior de la banda 1 (1e) hacia la banda 2, calculado por el método de las cuerdas.
c) Temperaturas que alcanzarían cada una de las bandas si no existiera la otra.
d) Plantear el balance térmico de la banda 2 (teniendo en cuenta la 1).
e) Si se obliga a que T1=300 K, calcular T2 y el valor de cada término del balance anterior.
f) Balance energético de la banda 1 en el caso anterior.
g) Temperaturas de ambas bandas en el caso de no forzar la temperatura de la banda 1.
Datos:
| > | read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):#with(RealDomain):assume(Ts4>0): |
| > | dat:=[R1=0.02*m_,R2=0.04*m_,E=1361*W_/m_^2,Tinf=2.7*K_,T1fix=300*K_];dat:=op(dat),Const,SI2,SI1: |
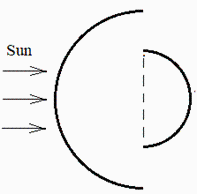
a) Factor de vista desde la cara interior de la banda 1 (1i) hacia la banda 2, por razonamiento deductivo basado en el álgebra de los factores de vista.
Sea 1d la superficie diametral del cilindro 1. En el recinto entre 1d y 1i, toda la radiación que sale de 1d va a 1i y por tanto F1d1i=1, y por reciprocidad F1i1d=A1d·F1d1i/A1i=2·1/pi=0,64: luego como F1i2=F1i1d=0,64.
| > | eqProject:=F1i2=F1i1d;eqRecipr:=A1i*F1i1d=A1d*F1d1i;eqA1i:=A1i=Pi*R1;eqA1d:=A1id=2*R1;F1d1i=1;F1i2=2/Pi;F1i2_:=evalf(2/Pi);F1i1i=1-F1i2;F1i1i=1-2/Pi;F1i1i:=evalf(rhs(%)); |
| (1) |
i.e. el 64 % de lo que emite 1i va a 2, y el otro 36 % es recibido por la misma superficie (F1i1i=1-F1i1d=0,36).
b) Factor de vista desde la cara exterior de la banda 1 (1e) hacia la banda 2, calculado por el método de las cuerdas.
Sean 1' y 1" los puntos extremos de la semicircunferencia 1, y 2' y 2" los de la 2. El método de las cuerdas (crossed-string) enseña a calcular los factores de vista bidimensionales como:
| > | eqF12bidim:=F12=(Cross1+Cross2-Stright1-Stright2)/(2*Length1);eqF12:=F12=(L1p2s+L1s2p-L1p2p-L1s2s)/(2*L1p1s);with(plots): |
| (2) |
caso A:  Caso B:
Caso B: 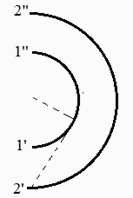
pero hay que llevar cuidado con la numeración para no confundir los dos casos expuestos en la figura anterior (en cualquier caso, el ángulo central es de 60º ya que es arccos(R1/R2)=arccos(1/2)=60º).
Si resolvemos el caso segundo, las longitudes de las cuerdas (y la del emisor) son:
| > | L1p2s=L1s2p;L1s2p:=sqrt(R2^2-R1^2)+2*Pi*R1/3;L2s1p_:=evalf(subs(dat,SI0,%))*m_;L1p2p=L1s2s;L1p2p:=(R2-R1);L1p2p_:=subs(dat,%);L1p1s:=Pi*R1;L1p1s_:=subs(dat,%);eqF12_:=subs(L1p2s=L1s2p,L1s2s=L1p2p,dat,SI0,eqF12);F1e2_:=1-rhs(%); |
| (3) |
i.e. para el caso B, F12=0,90, i.e. el 90 % de lo que emite la superficie convexa de 1 va a 2, por lo que el otro 10 % saldría por la zona diametral abierta hacia el vacío de fondo del Universo (nodo 3), lo que coincidirá con lo que vamos buscando: lo que emite la cara 1e y llega a 2 en el caso A de la figura anterior.
Si queremos resolver directamente el caso A, tendríamos que intercambiar 1' con 1" (si no lo hiciéramos nos saldría F12=0,90, pero nos daríamos cuenta de que no puede ser porque ha de ser menor de 1/2 ya que F13>>F12.
Conclusión, F1e2=0,10.
Este factor de vista también se podría haber determinado por combinación de las caras 1e y 1a del cilindro macizo 1 con la superficie 2.

Como el global es F12=1/2 (por simetría), y hemos calculado F1a2=(sqrt(3)+Pi-arccos(1/2)-1)/Pi, podemos determinar F1e2 asÍ:
| > | eqDistrib:=(A1e+A1a)*F12=A1e*F1e2+A1a*F1a2;F1e2:=((A1e+A1a)*F12-A1a*F1a2)/A1e;F12=1/2;F1a2:=(sqrt(3)+Pi-arccos(1/2)-1)/Pi;F1a2_:=evalf(%);F1e2__:=subs(F12=1/2,A1e=Pi,A1a=Pi,F1e2);F1e2__:=evalf(%); |
 |
|
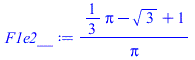 |
|
| (4) |
c) Temperaturas que alcanzarían cada una de las bandas si no existiera la otra.
Si están solas quedarán a la misma temperatura porque el balance energético es el mismo (si son cuerpos negros, que si no no; e.g. si todas fuesen blancas, la banda que recibiera el sol por la parte cóncava se calentaría más por reflexión solar).
| > | eqBE2:=m2*c2*dT2/dt=Qin2-Qout2;eqBE2:=0=Af2*E-A2*(1+F2i_inf)*sigma*T2^4;F2i_inf=1-F2i2i;F2i2i=1-2/Pi;F2i2i_:=evalf(rhs(%));eqBE2:=0=E*2*R-Pi*R*(2-F2i2i)*sigma*T^4;T=(2*E/(Pi*(2-F2i2i)*sigma))^(1/4);T_:=evalf(subs(F2i2i=F2i2i_,dat,SI0,rhs(%)))*K_;'T_'=TKC(%); |
| (5) |
i.e. en ambos casos quedaría la banda a 38 ºC. Se absorbe una potencia distinta, proporcional al área frontal, Qin=Af·E, y en ambos casos se emite por la cara convexa A·sigma·T^4, pero por la cara cóncava A·Finf·sigma·T^4, siendo Finf la fracción que va al vacío, que como se vio en el apartado primero es solo el 64 % pues el otro 36 % se reabsorbe en la misma superficie.
d) Plantear el balance térmico de la banda 2 (teniendo en cuenta la 1).
Ahora la banda 2 quedará más caliente de los 310 K porque recibe algo de calor de la banda 1, i.e. de ese 64 % de la emisión de la cara interior (2e) que antes iba al vacío, ahora irá una parte a la banda 1 (principalmente a su cara interna, 1i, y muy poco a la externa, 1e).
| > | eqBE2:=Qin2=Qout2;Qin2=E*2*R2;Qout2:=Qout2e+Qout2i;Qout2e:=A2e*sigma*(T2^4-Tinf^4);Qout2i:=Qout2i1+Qout2i_inf;Qout2i1:=A2i*F2i1*sigma*(T2^4-T1^4);Qout2i_inf:=A2i*F2i_inf*sigma*(T2^4-Tinf^4); |
| (6) |
donde conocemos casi todo, pero faltan algunos factores de vista:
| > | Qin2_:=subs(dat,SI0,E*2*R2)*W_/m_;Qout2e_:=subs(A2e=Pi*R2,dat,SI0,Qout2e);Qout2i1_:=subs(A2i=Pi*R2,dat,SI0,Qout2i1);Qout2i_inf_:=subs(A2i=Pi*R2,dat,SI0,Qout2i_inf);eq2i1:=F2i1=F2i2i+F2i1;eq2i:=F2i1+F21_inf=1; |
| (7) |
aunque son fáciles de calular:.
| > | F2i1:=F2i1i+F2i1e;F2i1i:=A1i*F1i2i/A2i;F2i1i:=Pi*R1*F1i2i/(Pi*R2);F1i2=F1i2_;F2i1i_:=subs(F1i2i=F1i2,%,dat,F2i1i);F2i1e:=A1e*F1e2i/A2i;F2i1e:=Pi*R1*F1e2i/(Pi*R2);F1e2=F1e2_;F2i1e_:=subs(F1e2i=F1e2,%,dat,F2i1e);F2i1_:=subs(F1i2i=F1i2_,F1e2i=F1e2_,dat,F2i1);F2i_inf_:=1-F2i1_-F2i2i_; |
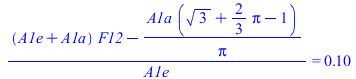 |
|
 |
|
| (8) |
i.e. de la cara externa de la banda 2, todo va al infinito, pero de la cara interna (2i), una fracción F2i1=0,37 va a la banda 1 (casi todo a la parte cóncava, F2i1i=0,32, y un poco a la trasera, F2i1e=0,05), y el resto (63 %) se reparte entre la reabsorción en la misma cara 2i (F2i2i=F1i1i=0,36 antes calculado) y lo que sale por los laterales hacia el infinito, F2i_inf=0,27.
e) Si se obliga a que T1=300 K, calcular T2 y el valor de cada término del balance anterior..
Sustituyendo valores en los términos del balance térmico, queda:
| > | 'Qout2e_'=Qout2e_;Qout2i1__:=subs(T1=T1fix,F1i2i=F1i2_,F1e2i=F1e2_,dat,SI0,Qout2i1_);Qout2i_inf__:=subs(F2i_inf=F2i_inf_,Qout2i_inf_);eqBE2:=Qin2=Qout2;eqBE2_:=subs(SI0,Qin2_)=Qout2e_+Qout2i1__+Qout2i_inf__;T2_:=fsolve(%,T2=100..500)*K_;'T2_'=TKC(%);Qout2e__:=subs(T2=T2_,SI0,Qout2e_);Qout2i1_:=subs(T2=T2_,SI0,Qout2i1__);Qout2i_inf_:=subs(T2=T2_,SI0,Qout2i_inf__);Qout2_:=(Qout2e__+Qout2i1_+Qout2i_inf_)*W_/m_; |
| (9) |
i.e. si la T1 se mantiene en 300 K (27 ºC), la T2 alcanza 325 K (52 ºC) absorbiendo 109 W/m de radiación solar, y emitiendo 80 W/m al vacío por delante, 21 W/m al vacío por detrás, e intercambiando 8 W/m netos con la banda 1.
Nótese que probablemente habrá que alimentar eléctricamente la banda 1 para mantenerla a 300 K.
f) Balance energético de la banda 1 en el caso anterior.
La banda 1 no estará en equilibrio radiativo; su balance energético será:
| > | eqBE1:=Qin1=Qout1;Qin1:=Qin12+Qin1ele;Qin12:='Qout2i1';Qin12_:=subs(A2i=Pi*R2,F1i2i=F1i2_,F1e2i=F1e2_,dat,SI0,Qout2i1);Qin12__:=subs(T1=T1fix,T2=T2_,dat,SI0,%);Qout1:=Qout1_inf;Qout1_inf:=A1*F1_inf*sigma*(T1^4-Tinf^4);F1_inf=1-F12;F12:=A2i*'F2i1'/A1;'F2i1'=F2i1_;A1=2*A1e;eqA1:=subs(A1e=Pi*R1,dat,%);F12_:=subs(dat,Pi*R2*F2i1_/(Pi*R1));F1_inf_:=1-%;Qout1_inf_:=subs(eqA1,F1_inf=F1_inf_,dat,SI0,Qout1_inf);Qout1_inf__:=subs(T1=T1fix,dat,SI0,Qout1_inf_);Q1inele_:=subs(T1=T1fix,dat,SI0,Qout1_inf_-Qin12__)*W_/m_; |
| (10) |
i.e. si la banda 1 está a 300 K, ha de recibir 7 W/m por su interior (resistencias eléctricas), ya que emite al vacío 15 W/m y solo recibe 8 W/m de la banda 2 que está a 325 K.
g) Temperaturas de ambas bandas en el caso de no forzar la temperatura de la banda 1.
Los dos balances son ahora:
| > | eqBE2_:=eqBE2;eqBE2__:=subs(Qin2=E*2*R2,A2e=Pi*R2,A2i=Pi*R2,F1i2i=F1i2_,F1e2i=F1e2_,F2i_inf=F2i_inf_,dat,SI0,%);eqBE1_:=eqBE1;eqBE1__:=subs(Qin1ele=0,eqA1,A2i=Pi*R2,F1_inf=F1_inf_,F1i2i=F1i2_,F1e2i=F1e2_,F2i_inf=F2i_inf_,dat,SI0,%);sol_:=fsolve({eqBE1__,eqBE2__},{T1,T2},T1=100..500,T2=100..500);T1_:=subs(sol_,T1)*K_;T2_:=subs(sol_,T2)*K_; |
| (11) |
i.e., si no se alimenta eléctricamente, la banda 1 quedaría a 281 K (en vez de a los 300 K anteriores, o a los 310 K si estuviera sola), y la banda 2 no llegaría a 325 K sino a 322 K (o a los 310 K si estuviera sola).
| > |