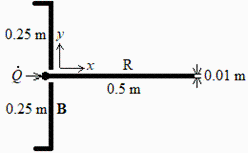
Fig. 1. Esquema de perfil del radiador desplegado (R) y la pared vista del cuerpo (B), y dimensiones.
| > | restart:#"m13_p67" |
Para evacuar 500 W de calor en una aplicación espacial, considérese un radiador R que sobresale del cuerpo del satélite B como se indica en la figura, donde se muestran las dimensiones transversales de R (Lx=0,5 m, =0,01 m) y de B (Ly=0,25 m). Suponiendo que la temperatura de R se mantiene a 15 ºC (con un flujo bifásico por su interior), que la de B va a ser 30 ºC, que puede despreciarse el acoplamiento conductivo entre R y las paredes de B, que la emisividad de todas las superficies es =0,9, y que no queda a la vista de R ningún otro cuerpo, se pide:
a) Factores de vista entre R y B, en el límite bidimensional (método de las cuerdas).
b) Plantear el balance térmico del radiador, y calcular la anchura del radiador, Lz, necesaria para evacuar ese calor (empezar con el modelo de cuerpo negro).
c) Intercambio radiativo de R y B.
d) Ahora se va a considerar R dividido en dos mitades (la R0, próxima a la base, y la R1 más alejada). Plantear el balance térmico de cada parte de R.
e) Determinar los nuevos factores de vista (en el límite bidimensional).

Fig. 1. Esquema de perfil del radiador desplegado (R) y la pared vista del cuerpo (B), y dimensiones.
| > | read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):with(plots):with(RealDomain):assume(x>0): |
| > | su:="":dat:=[Qdot=250*W_,Lx=0.5*m_,Ly=0.25*m_,delta=0.01*m_,T1=(15+273.15)*K_,T2=(30+273.15)*K_,Tinf=2.7*K_,epsilon=0.9];dat:=op(dat),Const,SI2,SI1: |
a) Factores de vista entre R y B, en el límite bidimensional (método de las cuerdas).
El problema es simétrico, así que tomaremos solo un lado, i.e. sea 1 la cara superior de R, y 2 la cara contigua de B. Sea 3 el espacio vacío que se ve desde 1 (será F13=1-F12).
Por el método de las cuerdas, o buscando en la Tabla, se tiene:
| > | eqF12:=(Lx+Ly-0-sqrt(Lx^2+Ly^2))/(2*Lx);eqF12:=F[12]=((1+h)-sqrt(1+h^2))/2;eqh:=h=Ly/Lx;eqh_:=subs(dat,%);F12_:=evalf(subs(h=1/2,rhs(eqF12)));plot(rhs(eqF12),h=0..1,F[12]=0..0.5);eqF21:=F[21]=Lx*F[12]/Ly;F21_:=subs(dat,Lx*F12_/Ly);F13_:=1-F12_;F23_:=1-F21_; |
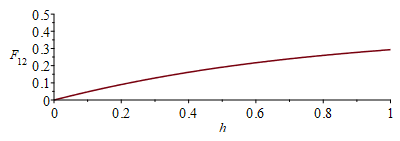 |
|
| (1) |
i.e. el 19 % de lo que sale de R llega a B (y el 38 % de lo que sale de B llega a R); por tanto, el radiador emite un 81 % directamente al espacio vacío. Se ha representado F12 (desde R hasta B) en variable h=B/A (se podría haberlo hecho en función de R/B y no de B/R). El factor de vista tridimensional con esa anchura se puede ver que es F12=0,18 en lugar de 0,19 (en la Tabla).,
b) Plantear el balance térmico del radiador suponiendo cuerpos negros, y calcular la anchura del radiador, Lz, necesaria para evacuar ese calor.
Conviene empezar simplificando todo lo posible, suponiendo cuerpos negros, y despreciando el efecto de B. Y poner Tinf=0.
| > | eqBE0:=C1*dT1/dt=Qdot-Qinf;eqBE0:=0=Qdot-Qinf;eqBE0:=0=Qdot-A*sigma*T1^4;A_:=subs(dat,solve(%,A));A=Lx*Lz;Lz0_:=subs(dat,A_/Lx); |
| (2) |
i.e. el radiador habría de tener una anchura de Lz=1,28 m si fuese negro y estuviese solo.
Con eps=0,9 sería:
| > | eqBE0:=0=Qdot-epsilon*A*sigma*T1^4;A_:=subs(dat,solve(%,A));A=Lx*Lz;Lz0_:=subs(dat,A_/Lx); |
| (3) |
Si se tiene en cuenta el efecto de B, pero todavía como cuerpos negros, sería:
| > | eqBE1:=C1*dT1/dt=Qdot-Q12-Q13;Qdot=subs(dat,Qdot);eqQ12:=Q12=A1*F12*(M2-M1);eqQ13:=Q13=A1*F13*(M3-M1);eqM1:=M1=sigma*T1^4;eqM1_:=subs(dat,%);eqM2:=M2=sigma*T2^4;eqM2_:=subs(Const,dat,%);eqM3:=M3=sigma*Tinf^4;eqM3_:=subs(dat,%);eqBE:=0=Qdot-A1*F12*(M1-M2)-A1*F13*(M1-M3);eqBE_:=subs(eqM1_,eqM2_,eqM3_,F12=F12_,F13=F13_,dat,%);A1_:=subs(dat,solve(%,A1));eqLz:=Lz=A1/Lx;eqLz_:=subs(A1=A1_,dat,%); |
| (4) |
i.e. con la pantalla de B, el radiador habría de ser mas ancho: 1,67 m en vez de 1,28 m.
Nótese que solo estamos estudiando cómo disipar 500 W con el radiador; la base B ya de por sí (sin radiador) emitiría QB=eB·AB·sigma·TB^4=345 W (con esta Lz=1.67).
Si los cuerpos son grises hay que recurrir al método de las exitancias para determinar la nueva A1 y M1 y M2 (M3=M3bb). Las 3 ecuaciones son (sistema lineal):
| > | eq1:=A1*epsilon1*(M1-M1bb)/(1-epsilon1)=A1*F12*(M2-M1)+A1*F13*(M3-M1);eq2:=A2*epsilon2*(M2-M2bb)/(1-epsilon2)=A2*F21*(M1-M2)+A2*F23*(M3-M2);eq3:=A1*epsilon1*(M1-M1bb)/(1-epsilon1)=-Qdot;M3=0;eq1_:=subs(M1bb=rhs(eqM1_),M2bb=rhs(eqM2_),M3=0,epsilon1=epsilon,epsilon2=epsilon,F12=F12_,F13=F13_,F21=F21_,F23=F23_,dat,SI0,eq1);eq2_:=subs(A2=h*A1,eqh_,M1bb=rhs(eqM1_),M2bb=rhs(eqM2_),M3=0,epsilon1=epsilon,epsilon2=epsilon,F12=F12_,F13=F13_,F21=F21_,F23=F23_,dat,SI0,eq2);eq3_:=subs(M1bb=rhs(eqM1_),M2bb=rhs(eqM2_),M3=0,epsilon1=epsilon,epsilon2=epsilon,F12=F12_,F13=F13_,F21=F21_,F23=F23_,dat,SI0,eq3);sol_:=solve({eq1_,eq2_,eq3_},{A1,M1,M2});Lz_:=subs(sol_,dat,SI0,A1/Lx)*m_; |
| (5) |
Resolución del sistema paso a paso (despejando A1 de eq3, substituyendo en eq1, despejando M1, y substituyendo en eq2):
| > | eq1__:=simplify(subs(A1=solve(eq3_,A1),eq1_));eq2__:=simplify(subs(A1=solve(eq3_,A1),M1=solve(eq1__,M1),eq2_));eq2___:=numer(op(1,eq2__))=numer(op(2,eq2__));M2_=solve(%); |
| (6) |
En fin, teniendo todo en cuenta, la anchura necesaria sería de 1,82 m.
c) Intercambio radiativo de R y B.
| > | eqQ12;Q12_:=subs(sol_,F12=F12_,rhs(%));eqQ13;Q13_:=subs(sol_,F13=F13_,M3=0,rhs(%));eqQ21:=Q21=A2*F21*(M1-M2);Q21_:=subs(A2=A1*h,eqh_,sol_,F21=F21_,rhs(%));eqQ23:=Q23=A2*F23*(M3-M2);Q23_:=subs(A2=A1*h,eqh_,sol_,F23=F23_,M3=0,rhs(%)); |
| (7) |
i.e. el radiador R (1) recibe de B (2) un flujo neto de 15 W por cada cara (30 W en total), y emite 265 W por cada cara al espacio profundo (265=15+250). Se podría haber previsto que el calor iría de B a R y no de R a B.
La parte B pierde un flujo neto de 15 W hacia el radiador, y 125 W hacia el vacío; en total pierde 140 W que le han de llegar del interior para mantenerse a 30 ºC.
d) Ahora se va a considerar R dividido en dos mitades (la R0, próxima a la base, y la R1 más alejada). Plantear el balance térmico de cada parte de R.
Hay que especificar el acoplamiento conductivo/convectivo entre R0 y R1. Incluso aunque se mantuviera todo el radiador isotermo (T10=T11=15 ºC) y por tanto M10bb=M11bb, serían distintoas las exitancias M10 y M11 porque reflejarían distintos flujos. En el caso de cuerpos negros las ecuaciones nodales serían:
| > | eqBE10:=C10*dT10/dt=Qdot10+Q102-Q103;eqBE11:=C11*dT11/dt=Qdot11+Q112-Q113;eqQdot:=Qdot=Qdot10+Qdot11;eqQ102:=Q102=(A1/2)*F102*(M2-M1);eqQ103:=Q103=(A1/2)*F103*(M1-M3);eqQ112:=Q112=(A1/2)*F112*(M2-M1);eqQ113:=Q113=(A1/2)*F113*(M1-M3); |
| (8) |
Si no fuesen iguales T10 y T11, sería necesario conocer el acoplamiento entre nodos. Si no hubiese flujo másico entre ellos, sería Q1010=k*At*(T10-T11)/(Lx/2), siendo Q1011 el calor que va de 10 a 11, y Lx/2 la distancia entre nodos, pero nos dicen que hay un flujo bifásico por su interior, lo que complicaría el modelo.
e) Determinar los nuevos factores de vista (en el límite bidimensional).
Se pueden obtener usando la fórmula anterior del F12, pero pasando a F21.
| > | eqF12;eqFs:=F[2,´10+11´]=F[2,10]+F[2,11];eqF21:=F[2,1]=F21_;eqF210:=F[2,10]=evalf(subs(h=1,rhs(eqF12)));F210_:=rhs(%);eqF211:=F[2,11]=F[2,1]-F[2,10];F211_:=rhs(eqF21)-rhs(eqF210);F102_:=F210_;F112_:=F211_;F103_:=1-F102_;F113_:=1-F112_; |
| (9) |
i.e. la cara 10 radia un 29 % a la B y un 71 % al espacio, mientras que el trozo 11 radia un 9% a B y un 91 % al espacio. Se ha hecho uso de que A2=A10=A11.
ADICIONAL
Vamos a resolver los balances energéticos de cada parte (R0 y R1) con el modelo de cuerpos negros antes planteado.
Para la parte más cercana:
| > | eqQ102;subs(A1=A1_,F102=F102_,F103=F103_,eqM1_,eqM2_,eqM3_,dat,%);eqQ103;subs(A1=A1_,F102=F102_,F103=F103_,eqM1_,eqM2_,eqM3_,dat,%);eqBE10_:=subs(dT10=0,eqQ102,eqQ103,eqQ112,eqQ113,eqBE10);eqBE10__:=subs(A1=A1_,F102=F102_,F103=F103_,eqM1_,eqM2_,eqM3_,dat,%);Qdot10_:=solve(%,Qdot10); |
| (10) |
i.e. la parte R10 recibe 11 W de la base B, y emite 115 al espacio, por lo que para que el régimen sea estacionario debe recibir 115-11=105 W del inteior (no los 125 W que era la mitad de los 250 W de toda la cara superior).
Para la parte más alejada:
| > | eqQ112;subs(A1=A1_,F112=F112_,F113=F113_,eqM1_,eqM2_,eqM3_,dat,%);eqQ113;subs(A1=A1_,F112=F112_,F113=F113_,eqM1_,eqM2_,eqM3_,dat,%);eqBE11_:=subs(dT11=0,eqQ102,eqQ103,eqQ112,eqQ113,eqBE11);eqBE11__:=subs(A1=A1_,F112=F112_,F113=F113_,eqM1_,eqM2_,eqM3_,dat,%);Qdot11_:=solve(%,Qdot11); |
| (11) |
i.e. la parte R11 recibe 3 W de B, y emite 149 W al espacio, por lo que para que el régimen sea estacionario debe recibir 148,6-3,3=145 W del inteior (no los 125 W que era la mitad de los 250 W).
ADICIONAL
Determinar los factores de vista en el límite bidimensional, para una estrecha banda en el extremo del radiador.
Conviene cambiar de variable de h a x=1/h. Para obtener el nuevo F12 basta derivar adecuadamente:
| > | eqF12x:=subs(h=1/x,eqF12);eqx_:=x=subs(eqh_,1/h);F12x_:=subs(eqx_,rhs(eqF12x));eqF12dx:=F[12]=subs(h=x,diff(rhs(eqF12),h));F12dx_:=subs(eqx_,rhs(eqF12dx));plot([rhs(eqF12x),rhs(eqF12dx)],x=0..2,F[12]=0..0.5); |
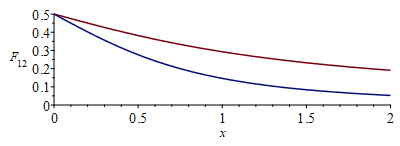 |
i.e. solo el 5 % de lo que saliese del dx más alejado llegaría a B. En la figura, en rojo el F12 en variable x=Lx/Ly (F12=0,19 para x=2), y en azul el F12 para todo el radiador (F12=0,053 para x=2).
ADICIONAL
Determinación del factor de vista de R a B en el caso tridimensional para la anchura calculada.
| > | Lx_Ly_Lz_:=subs(dat,[Lx,Ly,Lz_]);eqh:=h=Ly/Lz;eqh_:=subs(Lz=Lz_,dat,%);eqw:=w=Lx/Lz;eqw_:=subs(Lz=Lz_,dat,%);F12:=(1/(Pi*w))*(w*arctan(1/w)+h*arctan(1/h)-sqrt(w^2+h^2)*arctan(1/sqrt(w^2+h^2))+ln(a*b^(w^2)*c^(h^2))/4);a:=(1+w^2)*(1+h^2)/(1+w^2+h^2);b:=w^2*(1+w^2+h^2)/((1+w^2)*(w^2+h^2));c:=h^2*(1+h^2+w^2)/((1+h^2)*(h^2+w^2));F12tri:=evalf(subs(eqh_,eqw_,F12));plot(subs(h=0.25/z,w=0.5/z,F12),z=0..5,F[12]=0..0.2,color=black) |
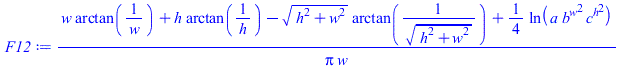 |
|
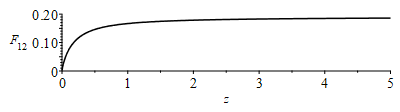 |
i.e. el factor de vista tridimensional desde R a B es F12=0,176, así que el valor bidimensional usado, F12=0,191, es bastante aproximado (y mucho más sencillo de calcular).
| > |