| > | restart:#"m13_p63" |
Se quiere estudiar la transmisión de calor entre un pequeño disco plano de radio R1 y un gran disco plano paralelo y coaxial, de radio R2 y a una distancia H del anterior, en el vacío. Para ello se va a considerar el recinto formado por las siguientes cuatro superficies: los dos discos 1 y 2, el anillo (superficie 3) en el plano del disco 1 que se extiende de R1 a R2, y la banda cilíndrica lejana (superficie 4) que completa un recinto. Se quiere evaluar los resultados para R1=0,1 m, R2=10 m, y H=1 m, T1=300 K, T2=250 K, y T3=T4=3 K. Se pide:
a) Factores de vista F12, F13, F14, y F21, F23 y F24 (para el límite R2/R1>>1, el factor de vista de 1 a 2 es F12=sin2=1/(1+(H/R2)2), siendo el ángulo del semicono que abarca el disco 2 desde el 1).
b) Flujos radiativos e intercambio de calor entre 1 y 2 con el modelo de cuerpos negros.
c) Flujos radiativos e intercambio de calor entre 1 y 2 en el límite R1<<R2>>H, y ambos discos con emisividad =0,1.
d) Flujos radiativos e intercambio de calor entre 1 y 2 en el límite R1=R2>>H, y ambos discos con emisividad =0,1.
e) Plantear las ecuaciones para resolver el problema por el método de las exitancias, para el caso de superficies grises en el límite R1<<H<<R2 (i.e. sin tener en cuenta la superficie 4).
read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):with(plots):with(RealDomain):assume(x>0):
| > | su:="":dat:=[R1=0.1*m_,R2=10*m_,H=1*m_,T1=300*K_,T2=250*K_,T3=0,T4=0,epsilon=0.1];dat:=op(dat),Const,SI2,SI1: |
a) Factores de vista F12, F13, F14, y F21, F23 y F24 (para el límite R2/R1>>1, el factor de vista de 1 a 2 es F12=sin2=1/(1+(H/R2)2), siendo el ángulo del semicono que abarca el disco 2 desde el 1).
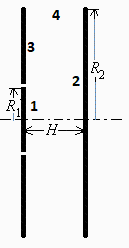
| > | F12:=sin(alpha)^2;F12:=1/(1+(H/R2)^2);F12_:=evalf(subs(dat,%));F13=0;F14='1-F12';F14_:=1-F12_;F12__:=F12_:F21:='A1*F12/A2';F21_:=subs(A1=Pi*R1^2,A2=Pi*R2^2,dat,%);F23:='1-F21';F23_:=1-F21_;F24:=0; |
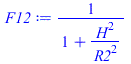 |
|
| (1) |
i.e. F11=0, F12=0,99, F13=0, F14=0,01 y F21=0,001, F23=0,9999, F24=0, aunque en este límite no se pueden separar las superficies 3 y 4 y deberíamos poner F2,3+4=0,9999.
ADICIONAL. Como en la Tabla viene una expresión general válida para cualesquiera valores, vamos a ver la diferencia
| > | F12:=(r12_-sqrt(r12_^2-4*r12))/2;r12:=(r2/r1)^2;r12_:=1+1/r1^2+r12;r1:=R1/H;r2:=R2/H;r1_:=subs(dat,r1);r2_:=subs(dat,r2);F12_:=subs(dat,F12);Dif:=F12__-F12_;F21_:=subs(A1=Pi*R1^2,A2=Pi*R2^2,dat,F21);F24:=(sqrt(4*r^2+1)-1)/(2*r^2);r:=R2/H;F24_:=evalf(subs(dat,F24));F23:='1-F21-F24';F23_:=1-F21_-F24_;F23:='F23': |
| (2) |
i.e. por un lado vemos que la diferencia en el cálculo de F12 (1 ppm) es totalmente despreciable. Por otra parte, ahora vemos que no era correcta la asignación F23=1,F24=0; aunque la suma es verdad que coincide (F2,3+4=0,9999), ahora vemos que ambos son apreciables: F24=0,10 y F23=0,90.
Curiosidad: ¿cuándo empezará a ser notable la diferencia en el cálculo de F12 por ambos métodos; e.g. cuánto valdrá para R1=R2=H?
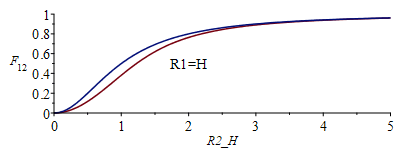
| > | F12cone:=1/(1+(H/R2)^2);F12cone_111:=subs(R1=1,R2=1,H=1,F12cone);F12_111:=evalf(subs(R1=1,R2=1,H=1,F12));p:=plot(subs(R1=1,H=1,R2=R2_H,[F12,F12cone]),R2_H=0..5,F[12]=0..1):pt:=textplot([2,0.5,"R1=H"]):display({p,pt});p:=plot(subs(R1=1,R2=1,H=H_R2,[F12,F12cone]),H_R2=0..5,F[12]=0..1):pt:=textplot([2,0.5,"R1=R2"]):display({p,pt});F12:='F12': |
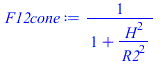 |
|
 |
|
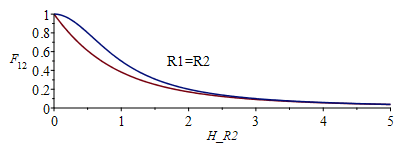 |
efectivamente la aproximación de F12 dada (la del seno) para R2/R1>>1 casi es buena para R1=R2 y cualquier H, como muestra la figura última, e incluso para R2/R1<1 si H>R1, como muestra la figura anterior; para discos iguales separados un radio (R =R2=H) la aproximación cónica de F12=0,50 y la real es F12=0,38.
b) Flujos radiativos e intercambio de calor entre 1 y 2 con el modelo de cuerpos negros.
| > | Q12:=A1*F12*(M2bb-M1bb);Q12:=A1*F12*sigma*(T2^4-T1^4);Q12_:=subs(A1=Pi*R1^2,F12=F12_,dat,%);Phi1:=A1*sigma*T1^4;Phi1_:=subs(A1=Pi*R1^2,dat,%);Phi1F12_:=Phi1_*F12_;Phi2:=A2*sigma*T2^4;Phi2_:=subs(A2=Pi*R2^2,dat,%);Phi2F21_:=Phi2_*F21_;F12:='F12': |
| (3) |
i.e. la cara 1 emite 14,4 W que prácticamente todo va a la 2 (14,3 W), mientras que la 2 emite 70 kW pero solo un 0,1 % va a la 1 (i.e. solo llegan 6,9 W que se absorben). El neto es 14,3-6,9=7,4 W. El calor (neto) que llega a R1 procedente de R2 es Q12=-7,4 W, negativo porque no entra sino que sale, al estar más caliente el R1 que el R2.
c) Flujos radiativos e intercambio de calor entre 1 y 2 en el límite R1<<R2>>H, y ambos discos con emisividad =0,1.
Este es el caso aplicable al intercambio IR con un planeta:
| > | Q12:=epsilon1*A1*F12*(epsilon2*sigma*T2^4-sigma*T1^4);Q12_:=subs(A1=Pi*R1^2,F12=F12_,epsilon1=epsilon,epsilon2=epsilon, dat,%);Phi1:=epsilon1*A1*sigma*T1^4;Phi1_:=subs(A1=Pi*R1^2,epsilon1=epsilon,epsilon2=epsilon, dat,%);Phi2:=epsilon2*A2*sigma*T2^4;Phi2_:=subs(A2=Pi*R2^2,epsilon1=epsilon,epsilon2=epsilon,dat,%);Phi2F21_:=Phi2_*F21_; |
| (4) |
i.e. sale neto 1,36 W de 1 a 2, que corresponde a una emisión de 1,44 W (toda hacia 2 porque 4 apenas cuenta), y una absorción de lo emitido por 2 (lo reflejado por 2, pese a que rho2=0,9, no cuenta si T3=0). El disco 2 emite 7 kW, de los cuales inciden 0,7 W sobre el disco 1 que absorbe 0,07 W (1,44-0,07=1,37 W).
d) Flujos radiativos e intercambio de calor entre 1 y 2 en el límite R1=R2>>H, y ambos discos con emisividad =0,1..
En este caso F12=1 y puede estudiarse como un recinto con dos únicos nodos:
| > | Q12:=(M2bb-M1bb)/((1-epsilon1)/(epsilon1*A1)+1/(A1*F12)+(1-epsilon2)/(epsilon2*A2));Q12:=subs(A1=A,A2=A,F12=1,epsilon1=epsilon,epsilon2=epsilon,M1bb=sigma*T1^4,M2bb=sigma*T2^4,%);Q12_:=subs(dat,Q12);Q12bb_:=subs(epsilon=1,dat,Q12);Q12__:=subs(A=Pi*R1^2,dat,Q12_);Q12bb__:=subs(A=Pi*R1^2,dat,Q12bb_);Q12bad:=A*epsilon1*epsilon2*sigma*(T2^4-T1^4);Q12bad_:=subs(A=Pi*R1^2,epsilon1=epsilon,epsilon2=epsilon,dat,%); |
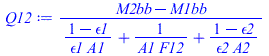 |
|
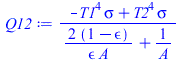 |
|
| (5) |
i.e. por unidad de área, la cara 1 evacuaría 12,5 W/m2 a la cara 2, apenas un 14 % de lo que transmitiría si fuesen cuerpos negros (evacuaría 238 W/m2). Si ahora consideramos solo un área de 0,1 m de radio, la cara 1 evacuaría 0,39 W en el caso e=0,1, y 7,47 W en el caso de cuerpos negros; la pequeña diferencia con el apartado b) (Q12=-7.40 W) se explica porque aquí el disco R2 es infinito y allí se consideró infinito. Los flujos emitidos por la parte pequeña de 1, y por 2, serán los mismos que antes porque no ha cambiado ni su eps ni su T.
Nótese que esta última expresión (Q12bad) es falsa (comparar con el apartado c).
e) Plantear las ecuaciones para resolver el problema por el método de las exitancias, para el caso de superficies grises en el límite R1<<H<<R2 (i.e. sin tener en cuenta la superficie 4).Superficie 1 (solo ve la 2):
| > | eq1:=Q1=e1*A1*(M1-M1bb)/(1-e1);eq1_:=Q1=A1*F12*(M2-M1); |
| (6) |
Superficie 2 (ve la 1 y la 3):
| > | eq2:=Q2=e2*A2*(M2-M2bb)/(1-e2);eq2_:=Q2=A1*F12*(M1-M2)+A2*F23*(M3bb-M2); |
| (7) |
Superficie 3 (solo ve la 2).
| > | eq3_:=Q3=A2*F23*(M2-M3bb); |
| (8) |
Esta ecuación solo nos serviría para calccular la radiación que escapa por 3, por lo que el problema puede reducirse a las 4 ecuaciones previas (eq1,eq1_,eq2,eq2_) con las 4 incógnitas (Q1,Q2,M1,M2) si también se considera dato T3. La solución es:
| > | sol:=solve({eq1,eq1_,eq2,eq2_},{Q1,Q2,M1,M2}); |
| (9) |
Podemos comprobar la solución con T3=0 y cuerpos negros (1 y 2):
| > | sol0:=subs(A1=Pi*R1^2,A2=Pi*R2^2,F12=F12_,F23=1,e1=epsilon,e2=epsilon,epsilon=1,M1bb=sigma*T1^4,M2bb=sigma*T2^4,M3bb=0,dat,sol); |
| (10) |
efectivamente, se recupera el valor Q1=Q12=-7,4 W.
Y la solución con T3=0 y cuerpos grises (e1=e2=0.1)
| > | sol01:=subs(dat,evalf(subs(A1=Pi*R1^2,A2=Pi*R2^2,F12=F12_,F23=1,e1=epsilon,e2=epsilon,M1bb=sigma*T1^4,M2bb=sigma*T2^4,M3bb=0,dat,sol))); |
| (11) |
efectivamente, se recupera el valor Q1=Q12=-1.36 W.
| > |