| > | restart:#"m13_p60.mw" |
| > | read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):with(plots):with(RealDomain): |
Una esfera maciza de 0,25 m de diámetro está disipando 30 W en un recinto evacuado cuyas paredes se mantienen a 20 ºC. Sobre la esfera incide una radiación solar de 800 W/m2, a través de una pequeña ventana. Se va a disponer un escudo semiesférico concéntrico con la esfera y de radio doble del de ésta, centrado en la dirección de la radiación incidente. Las propiedades termo-ópticas de la esfera maciza son =0,9,y =0,8, y las de la cáscara semiesférica son =0,4,y =0,8 por el exterior, y =0,4,y =0,4 por el interior. Considerando las superficies isotermas y difusas, se pide:
a) Temperatura de la esfera en ausencia del escudo.
b) Plantear las ecuaciones necesarias cuando está el escudo.
c) Factores geométricos de la superficie interior del escudo.
d) Temperaturas del escudo y de la esfera.
| > | dat:=[R1=0.125*m_,Wdis=30*W_,T0=(20+273)*K_,E=800*W_/m_^2,R2=0.25*m_,alpha1=0.9,epsilon1=0.8,alpha3=0.4,epsilon3=0.8,alpha2=0.4,epsilon2=0.4,T4=2.7*K_];dat:=op(dat),Const,SI2,SI1: |
| (1) |

a) Temperatura de la esfera en ausencia del escudo.
| > | eqEB:=C*dT/dt=Wdis+Qs-Qinf;eqEB:=0=Wdis+alpha1*E*Pi*R1^2-4*Pi*R1^2*epsilon1*sigma*(T^4-T0^4);eqEB_:=subs(dat,SI0,%);T_:=fsolve(eqEB_,T=10..1000)*K_;'T_'=TKC(%); |
| (2) |
i.e. la esfera alcanza 75 ºC.
b) Plantear las ecuaciones necesarias cuando está el escudo.
Usando el método de las radiosidades (exitancias), el circuito eléctrico equivalente, y las ecuaciones nodales son:
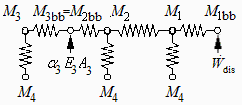
| > | eq1:=A1*epsilon1*(M1-M1bb)/(1-epsilon1)=A1*F12*(M2-M1)+A1*F14*(M4-M1);eq2:=A2*epsilon2*(M2-M2bb)/(1-epsilon2)=A2*F21*(M1-M2)+A2*F24*(M4-M2);eq3:=A3*epsilon3*(M3-M3bb)/(1-epsilon3)=A3*(M4-M3);eq4:=A1*epsilon1*(M1-M1bb)/(1-epsilon1)=-Wdis;eq5:=A2*epsilon2*(M2-M2bb)/(1-epsilon2)+A3*epsilon3*(M3-M3bb)/(1-epsilon3)+alpha3*E*A3/2=0;eqMbb:=Mbb=sigma*T^4;eqM4:=M4=sigma*T0^4;eqM4_:=subs(dat,%);M3bb=M2bb;eqA1:=A1=4*Pi*R1^2;eqA1_:=evalf(subs(dat,%));eqA2:=A2=2*Pi*R2^2;eqA2_:=evalf(subs(dat,%));A3=A2; |
| (3) |
Las eq1,eq2,eq3 son las radiaciones netas recibidas en las caras 1,2,3, mientras que las eq4 y eq5 son los balances térmicos globales en cada cuerpo.
c) Factores geométricos de la superficie interior del escudo.
Hay que calcular los factores con ayuda de la Table (Hemisphere).
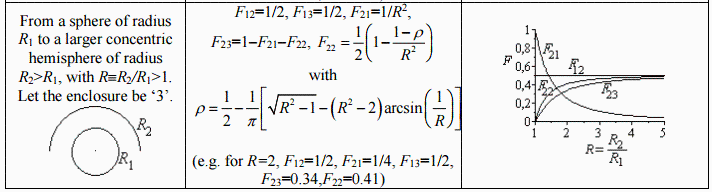
| > | F12_:=1/2;F14:=1-F12;F14_:=1-F12_;F21:=A1*F12/A2;F21_:=rhs(eqA1_)*F12_/rhs(eqA2_);F22:=(1-(1-rho)/R^2)/2;rho:=1/2-(sqrt(R^2-1)-(R^2-2)*arcsin(1/R))/Pi;R:=R2/R1;R:=subs(dat,%);F22_:=F22;F24:=1-'F22'-'F21';F24_:=1-F21_-F22_; |
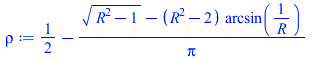 |
|
| (4) |
i.e. la cara 2 radia un 25 % a la esfera interior (F21=0,25), un 41 % sobre sí misma, y un 34 % hacia el recinto lejano.
d) Temperaturas del escudo y de la esfera.
Sustituyendo en las ecuaciones:
| > | eq1_:=subs(eqA1_,F12=F12_,eqM4_,dat,SI0,eq1);eq2_:=subs(eqA1_,eqA2_,F12=F12_,eqM4_,dat,SI0,eq2);eq3_:=subs(A3=A2,M3bb=M2bb,eqA1_,eqA2_,F12=F12_,eqM4_,dat,SI0,eq3);eq4_:=subs(eqA1_,eqA2_,F12=F12_,eqM4_,dat,SI0,eq4);eq5_:=subs(A3=A2,M3bb=M2bb,eqA1_,eqA2_,F12=F12_,eqM4_,dat,SI0,eq5);sol_:=solve({eq1_,eq2_,eq3_,eq4_,eq5_},{M1,M1bb,M2,M2bb,M3});T1_:=evalf(subs(sol_,dat,SI0,M1bb/sigma)^(1/4))*K_;'T1_'=TKC(%);T2_:=evalf(subs(sol_,dat,SI0,M2bb/sigma)^(1/4))*K_;'T2_'=TKC(%); |
| (5) |
i.e. con el escudo, queda T1=57 ºC (sin el escudo eran 75 ºC), y el escudo se pone a 46 ºC, todo ello dentro del recinto a 20 ºC, con la disipación en la esfera y la radiación solar en el escudo.
| > |