| > | restart:#"m13_p56" |
Para un estudio térmico preliminar de un apéndice de un satélite geoestacionario que consta de dos tubos de 30 mm de diámetro exterior, paralelos y en contacto, con una capacidad térmica de 250 J/K por metro de tubo, se pide:
a) Plantear el balance térmico de cada tubo, considerado cuerpo negro isotermo, cuando la dirección Sol-Tierra es perpendicular y está en el plano que forman los ejes de los dos cilindros, despreciando el acoplamiento conductivo entre ellos.
b) Resolver el caso anterior para régimen estacionario, suponiendo que el factor geométrico desde el tubo 1 al 2 fuese 1/3.
c) Calcular el factor geométrico entre los dos cilindros por el método de las cuerdas.
d) Factor geométrico entre las dos partes semicilíndricas enfrentadas, y comparación con el caso de dos bandas planas paralelas e iguales, de anchura igual al diámetro de los tubos y enfrentadas a igual distancia que los ejes.
e) Factor geométrico entre las partes convexas de las dos bandas semicilíndricas que quedarían al cortar la pareja de tubos por el plano que contiene sus ejes.
f) Estimar el tiempo de relajación térmica si se girase rápidamente 180º la pareja de tubos (para que le diera el sol al otro), y plantear las ecuaciones nodales de este transitorio.
Datos:
| > | read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):with(RealDomain):with(plots):#eq13_4;eq13_5;eq13_6; |
| > | dat:=[R=0.015*m_,E=1360*W_/(m_^2),C=250*J_/(m_*K_),RGEO=42.2e6*m_,RT=6.4e6*m_,Tinf=2.7*K_];dat:=op(dat),Const,SI2,SI1: |
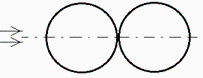
a) Plantear el balance térmico de cada tubo, considerado cuerpo negro isotermo, cuando la dirección Sol-Tierra es perpendicular y está en el plano que forman los ejes de los dos cilindros, despreciando el acoplamiento conductivo entre ellos.
Se puede despreciar el efecto de la Tierra (albedo e IR) por estar tan lejos (Rsat/RT=6,6); pero conviene evaluar el orden de magnitud de los términos que se desprecian. Planteamos el caso no estacionario, aunque solo resolveremos el estacionario (en la realidad, los transitorios suelen ser muy importantes).
Sea 1 el tubo que mira al Sol, 2 el tubo que mira a la Tierra, y 3 el espacio vacío de fondo (su temperatura, T=2,7 K, puede despreciarse frente a las demás). M es la exitancia o radiosidad. bb=blackbody.
A los intercambios netos de radiación entre dos superficies les llamaremos Qij aunque no sean cuerpos negros (pese a que con ello podría haber Qij≠0 con Ti=Tj, en contra de la definición de calor).
| > | eqBE1:=C1*dT1/dt=Q1s+Q1a+Q1p-Q12-Q13;eqBE2:=C2*dT2/dt=Q12+Q2a+Q2p-Q23;eqBE1:=C1*dT1/dt=E*Af1+A1*F1p*rho*E+A1*F1p*Mp-A1*F12*(Mbb1-Mbb2)-A1*(1-F12)*(Mbb1-Mbb3);eqBE2:=C2*dT2/dt=A1*F12*(Mbb1-Mbb2)+A2*F2p*rho*E+A2*F2p*Mp-A2*(1-F21)*(Mbb2-Mbb3);eqBE1:=C1*dT1/dt=E*2*R-2*Pi*R*F12*sigma*(T1^4-T2^4)-2*Pi*R*(1-F12)*sigma*T1^4;eqBE2:=C1*dT1/dt=2*Pi*R*F12*sigma*(T1^4-T2^4)-2*Pi*R*(1-F12)*sigma*T2^4; |
| (1) |
Estimación de las contribuciones por albedo e IR-terrestre en órbita geoestacionaria. Un valor superior sería el recibido por una placa plana enfrentada, cuyo factor geométrico es F12=(R/(R+H))^2, luego:
| > | eqh:=h=R[GEO]/R[T];eqh_:=subs(R[GEO]=RGEO,R[T]=RT,dat,%);eqF1p:=F1p=1/h^2;eqF1p_:=subs(eqh_,%);qs_qa_qp:=[E,F1p*rho*E,F1p*epsilon*sigma*Tp^4];E_rho_epsilon_Tp:=subs(dat,[E,0.30,0.62,288*K_]);qs_qa_qp_:=subs(rho=0.3,epsilon=0.62,Tp=288*K_,eqF1p_,dat,qs_qa_qp); |
| (2) |
i.e. como mucho el albedo sería un 9,3/1360=0,7 % de la irradiancia solar, y la IR todavía menor (5,6/1360), lo que confirma el prescindir de estos términos.
b) Resolver el caso anterior para régimen estacionario, suponiendo que el factor de vista de C1 a C2 fuese 1/3.
El problema es lineal en las M (o en T^4).
| > | eqBE1_:=evalf(expand(subs(F12=1/3,dT1=0,dat,eqBE1/R)));eqBE2_:=evalf(expand(subs(F12=1/3,dT1=0,dat,eqBE2/R)));sol:=solve(subs(T1^4=T14,T2^4=T24,[eqBE1_,eqBE2_]),{T14,T24});T1_:=subs(sol,SI0,sqrt(sqrt(T14)))*K_;'T1_'=TKC(%);T2_:=subs(sol,SI0,sqrt(sqrt(T24)))*K_;'T2_'=TKC(%); |
| (3) |
i.e. el tubo 1 quedaría a 31 ºC y el 2 a -42 ºC.
c) Calcular el factor geométrico entre los dos cilindros por el método de las cuerdas.
Sea 1 el primer cilindro, 2 el segundo, y 3 el entorno (recinto infinito). Usaremos el radio como unidad para adimensionalizar todas las geometrías.
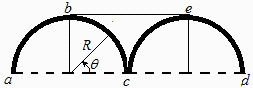
Como el problema es bidimensional, aplicamos el Método de las cuerdas (crossed string model). Solamente reciben radiación las partes enfrentadas, por lo que las cuerdas cruzadas irán desde el punto 'a', 'b', 'c', 'd', hasta 'f', y la simétrica (desde 'f' hasta 'g'); las cuerdas rectas irán directamente una desde 'a' hasta 'g' y la otra desde 'f' hasta 'e'. Nótese que si hubiésemos iniciado las cuerdas en otro punto (e.g. en los más opuestos), el resultado sería el mismo porque los tramos comunes se cancelarían. Sin embargo, para la longitud del cuerpo 1 hay que tomar exactamente la suya.
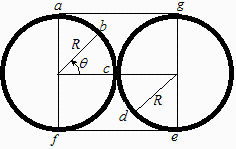
| > | eqF12didim:=F12=(Cross1+Cross2-Stright1-Stright2)/(2*Length1);eqF12didim_:=F12=(Cross-Straight)/(Length1);Cross_:=abcde;Cross_:=Pi*R;Straight_:=ag;Straight_:=2*R;Length1_:=2*Pi*R;eqF12didim__:=expand(subs(Cross=Cross_,Straight=Straight_,Length1=Length1_,eqF12didim_));evalf(%); |
| (4) |
i.e. era F12=0,182 (y no F12=1/3), como puede comprobarse en la Tabla para el caso "Parallel very-long external cylinders", lo que significa que sólo el 18 % de la radiación emitida difusamente por el cilindro isotermo 1 llega hasta el cilindro 2, que si es cuerpo negro la absorberá totalmente.
d) Factor geométrico entre las dos partes semicilíndricas enfrentadas, y comparación con el caso de dos bandas planas paralelas e iguales, de anchura igual al diámetro de los tubos y enfrentadas a igual distancia que los ejes.
Se trata de estas geometrías:
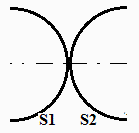
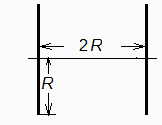
Entre las superficies enfrentadas S1 y S2, será muy parecido al caso anterior, cambiando a Length1=Pi*R; por tanto F12 sería el doble del anterior, i.e. el 36 % de la emisión del semicilindro S1 incidiría en el S2 (nótese que da igual si se considera el semicilindro S2 o el cilindro C2 completo).
Análogamente, para el caso de bandas planas paralelas iguales y enfrentadas, el método de las cuerdas da:
| > | F12_S1S2:=2*F12;Cross_:=sqrt(4+4)*R;Straight:=Straight_;Length1_:=2*R;eqF12didim__:=expand(subs(Cross=Cross_,Straight=Straight_,Length1=Length1_,eqF12didim_));evalf(%); |
| (5) |
i.e. entre bandas planas el 41 % de lo que emite la cara 1 (la superficie enfrentada, no la de detrás), llega a 2, mientras que en el caso de los semicilindros era el 36 %.
e) Factor geométrico entre las partes convexas de las dos bandas semicilíndricas que quedarían al cortar la pareja de tubos por el plano que contiene sus ejes.
Este problema puede resolverse por analogía con el primero (por simetría, la mitad del cilindro 1 emitirá la mitad del total, pero el área de emisión también es la mitad), o bien volviendo a aplicar el método de las cuerdas.
| > | F12_primero:=0.182;F12cuerdas:=(abcd+aced-abed-acd)/(abc);F12cuerdas_:=(2*(Pi+2)-(Pi+2)-4)/(2*Pi);'F12cuerdas_'=evalf(%); |
| (6) |
Efectivamente, da lo mismo que antes, F12=0,18.
f) Estimar el tiempo de relajación térmica si se girase rápidamente 180º la pareja de tubos (para que le diera el sol al otro), y plantear las ecuaciones nodales de este transitorio.
Linealizando el balance energético para un enfriamiento radiativo en el espacio:
| > | eqBE:=C*dT/dt=-epsilon*A*sigma*T^4;eqBE:=C*dT/dt=-4*epsilon*A*sigma*Tmean^3*(T-Tinf);sol:=T=Tini*exp(-4*2*Pi*R*sigma*Tmean^3/C);tc:=C/(4*2*Pi*R*sigma*Tmean^3);Tmean:=((T1ini^4+Tinf^4)/2)^(1/4);Tmean_:=subs(T1ini=T1_,dat,SI0,%)*K_;tc_:=subs(T1ini=T1_,dat,SI0,tc)*s_; |
| (7) |
i.e. al cabo de unos 700 s ya se habrá reducido la diferencia a más de la mitad, aunque tardaría varias veces más en reducirse la diferencia hasta un 1% o así, dada la dependencia con T^4).
Otro procedimiento, más sencillo pero menos aproximado, sería despreciar las pérdidas y calcular cuanto tardaría la radiación solar en calentar ul tubo 2 desde T1 hasta T2.
| > | eqBE:=C*dT/dt=E*Af;tc:='C*(T1_-T2_)/(E*2*R)';tc_:=subs(dat,%); |
| (8) |
i.e. unos 450 s; esta es una estimación por abajo, al haber despreciado las pérdidas de calor, que ralentizarían el proceso. La solución exacta es:
| > | eqBE1;eqBE2;eqBE2new:=C2*diff(T2(t),t)=E*2*R-2*Pi*R*F12*sigma*(T2(t)^4-T1(t)^4)-2*Pi*R*(1-F12)*sigma*T2(t)^4;eqBE1new:=C1*diff(T1(t),t)=2*Pi*R*F12*sigma*(T2(t)^4-T1(t)^4)-2*Pi*R*(1-F12)*sigma*T1(t)^4;eqBE2new_:=evalf(subs(C2=C,F12=F12cuerdas_,dat,SI0,eqBE2new));eqBE1new_:=evalf(subs(C1=C,F12=F12cuerdas_,dat,SI0,eqBE1new));sol0_:=solve(subs(T1(t)=T1,T2(t)=T2,[0=rhs(eqBE2new_),0=rhs(eqBE1new_),T1>0,T2>0]),[T1,T2]);T1ini:=subs(op(sol0_),T2)*K_;T2ini:=subs(op(sol0_),T1)*K_;sol_:=dsolve({eqBE1new_,eqBE2new_,T1(0)=T1ini/K_,T2(0)=T2ini/K_},numeric,{T1(t),T2(t)},'range'=0..5000);odeplot(sol_,[[t,T1(t)],[t,T2(t)]],t=0..3000); |
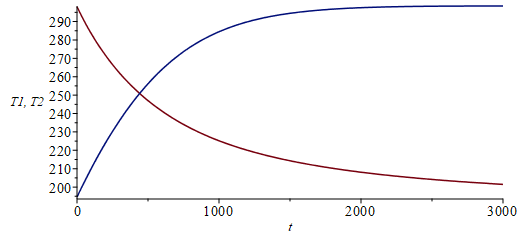 |
i.e. el tubo iluminado alcanza el nuevo equilibrio tras unos 2000 s, mientras que el que queda a la sombra tarda bastante más en enfriarse, aunque en ambos casos el intervalo ya se ha reducido a la mitad al cabo de unos 10 minutos (unos 500 s, como se estimó).
| > |