| > | restart:#"m13_p55" |
Para un estudio térmico preliminar, se va a considerar una nave espacial esférica de radio R, con un escudo térmico plano circular de radio R enfrentado al Sol a una distancia de 0,5 ua. La distancia entre centros del disco y la esfera es 2R, estando unidos por un mástil central de conductancia térmica KA. Se pide:
a) Plantear los balances térmicos de las dos piezas, comentando la idoneidad del modelo de dos nodos.
b) Factores geométricos involucrados.
c) Temperaturas estacionarias para esa configuración, suponiendo cuerpos negros y despreciando KA.
d) Desde el estado anterior, tiempo que tardaría la esfera en aproximarse al nuevo estado estacionario si desapareciera el escudo.
e) Hacer aplicación numérica para R=2 m y una capacidad térmica de la esfera C=100 kJ/K.
Datos:
| > | read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):with(plots): |
| > | su:="":dat:=[R=2*m_,C=100e3*J_/K_,r=0.5,E=1360*W_/m_^2,R[ST]=150e9*m_,alpha=0.5,epsilon1=0.9,epsilon2=0.2];dat:=op(dat),Const,SI2,SI1: |
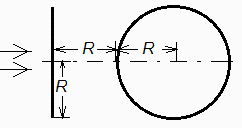
a) Plantear los balances térmicos de las dos piezas, comentando la idoneidad del modelo de dos nodos.
Nomen.: 1=disco, 2=esfera, 3=vacío de fondo, 10=cara iluminada del disco, 11=cara trasera.
El modelo de dos nodos supone que las conductividades térmicas de ambas piezas van a ser tan altas que todo el disco podrá suponerse que está a una sola temperatura, y lo mismo para la esfera. Sin embargo, parece que un buen diseño trataría de minimizar la conductividad del escudo, para proteger mejor (no irradiar mucho a la esfera), en cuyo caso convendría usar un modelo de al menos tres nodos (10, 11, y 2). También convendría dividir la esfera en varios nodos porque la parte delantera estará más caliente que la trasera.
Además, el tamaño finito del disco solar (semiángulo de 0,27º) iluminaría en penumbra la parte más externa de la esfera.
A los intercambios netos de radiación entre dos superficies les llamaremos Qij aunque no sean cuerpos negros (pese a que con ello podría haber Qij≠0 con Ti=Tj, en contra de la definición de calor).
| > | eqBE1:=m[1]*c[1]*dT[1]/dt=Q[s]-Q[10]-Q[12]-Q[13]-Qc[12];eqBE2:=m[2]*c[2]*dT[2]/dt=Qc[21]+Q[21]+Q[23];eqBE1:=m[1]*c[1]*dT[1]/dt=alpha[10]*E[10]*A[10]-epsilon[10]*A[10]*sigma*T[1]^4-(M[11]-M[2])*A[11]*F[11,2]-(M[11]-M[3])*A[11]*F[11,3]-KA*(T[1]-T[2])/R;eqBE2:=m[2]*c[2]*dT[2]/dt=(M[11]-M[2])*A[2]*F[2,11]+(M[3]-M[2])*A[2]*F[2,3]+KA*(T[1]-T[2])/R;eqM:=M=epsilon*sigma*T^4-rho*E; |
| (1) |
donde Qs es el 'calor' solar absorbido, Q10 es el radiado hacia delante, Q12 el intercambio de 1 a 2 (cara 11) por radiación, Q12c por conducción..., E es la irradiancia y M es la exitancia (radiosidad).
Podría pensarse que la reflexión infrarroja será despreciable frente a la emisión (rho*E<<M), pero eso no puede ser válido para el cuerpo 2 porque la absorción infrarroja y la emisión infrarroja están directamente ligadas porque alphaIR=epsilonIR. Para el modelo de cuerpos negros basta poner alpha=epsilon=1.
b) Factores geométricos involucrados.
De la Tabla de factores geométricos se obtiene:
| > | eqF11_2:=F[11,2]=2*r[1]^2*(1-1/sqrt(1+1/h^2));r=1,h=2;eqF11_2:=F[11,2]=evalf(2*(1-1/sqrt(1+1/2^2)));eqF2_11:=F[2,11]=A[11]*F[11,2]/A[2];A[11]=Pi*R^2,A[2]=4*Pi*R^2;eqF2_11:=F[2,11]=rhs(eqF11_2)/4;eqF2_3:=F[2,3]=1-F[2,11];eqF2_3:=F[2,3]=1-rhs(eqF2_11);eqF10_3:=F[10,3]=1;eqF11_3:=F[11,3]=1-F[11,2];eqF11_3:=F[11,3]=1-rhs(eqF11_2); |
![F[11, 2] = `+`(`*`(2, `*`(`^`(r[1], 2), `*`(`+`(1, `-`(`/`(1, `*`(`^`(`+`(1, `/`(1, `*`(`^`(h, 2)))), `/`(1, 2))))))))))](images/p551_8.gif) |
|
| (2) |
i.e. de la cara 11 a 2 el factor geométrico es 0,21 (i.e. el 21 % de la radiación que sale de 11 incide sobre 2), y el opuesto es F2,11=0,05 (i.e. sólo el 5 % de la radiación que sale de la esfera incide en el disco).
c) Temperaturas estacionarias para esa configuración, suponiendo cuerpos negros y despreciando KA.
Las ecuaciones nodales (balances energéticos) quedan:
| > | eqBE1_:=0=E[10]*A[10]-A[10]*sigma*T[1]^4-sigma*(T[1]^4-T[2]^4)*A[11]*F[11,2]-sigma*T[1]^4*A[11]*F[11,3];eqBE2_:=0=sigma*(T[1]^4-T[2]^4)*A[2]*F[2,11]-sigma*T[2]^4*A[2]*F[2,3]; |
| (3) |
La irradiancia solar disminuye con el cuadrado de la distancia, y a 0,5 ua es:
| > | eqEr:=E(r)=E(R[ST])/r^2;eqEr_:=E[10]=subs(dat,E/r^2); |
| (4) |
Dividiendo por A=Pi*R^2 y por sigma, con A2=4*A, y cambiando a variables T14=T1^4 y T24=T2^4, queda:
| > | eqBE1__:=0=E[10]/sigma-T[1]^4-(T[1]^4-T[2]^4)*F[11,2]-T[1]^4*F[11,3];eqBE2__:=0=(T[1]^4-T[2]^4)*4*F[2,11]-T[2]^4*4*F[2,3];eqBE_1:=0=E[10]/sigma-T14-(T14-T24)*F[11,2]-T14*F[11,3];eqBE_2:=0=(T14-T24)*4*F[2,11]-T24*4*F[2,3];sol:=expand(subs(F[11,3]=1-F[11,2],F[2,3]=1-F[2,11],F[11,2]=4*F[2,11],solve({eqBE_1,eqBE_2},{T14,T24})));T1_:=subs(sol,eqEr_,eqF2_11,dat,SI0,T14^(1/4))*K_;T2_:=subs(sol,eqEr_,eqF2_11,dat,SI0,T24^(1/4))*K_; |
![{T14 = `/`(`*`(E[10]), `*`(sigma, `*`(`+`(`-`(`*`(4, `*`(`^`(F[2, 11], 2)))), 2)))), T24 = `/`(`*`(E[10], `*`(F[2, 11])), `*`(sigma, `*`(`+`(`-`(`*`(4, `*`(`^`(F[2, 11], 2)))), 2))))}](images/p551_27.gif) |
|
| (5) |
i.e. el disco alcanzaría 469 K, y la esfera 225 K.
d) Desde el estado anterior, tiempo que tardaría la esfera en aproximarse al nuevo estado estacionario si desapareciera el escudo.
El nuevo estado estacionario sin escudo sería (A20 es el área proyectada de A2):
| > | eqBE20:=0=E[10]*A[20]-A[2]*sigma*T[2]^4;eqBE20:=0=E[10]/sigma-4*T[2]^4;T20_:=evalf(subs(eqEr_,dat,SI0,(E[10]/(4*sigma))^(1/4)))*K_; |
| (6) |
i.e. la esfera alcanzaría 394 K sin escudo. El transitorio sería:
| > | eqBE:=C*diff(T(t),t)=E[10]*A[20]-A[2]*sigma*T(t)^4;eqBE_:=evalf(subs(A[20]=Pi*R^2,A[2]=4*Pi*R^2,eqEr_,dat,SI0,%)); |
| (7) |
la cual se integra fácilmente a partir de la condición inicial T(0)=T2_=225 K hasta los 394 K finales. Una primera estimación del tiempo de relajación se obtiene en base al calentamiento inicial:
| > | eqini:=C*(T20-T2)/t_ini=E[10]*A[20]-A[2]*sigma*T(0)^4;t_ini:=C*(T20-T2)/(E[10]*A[20]-A[2]*sigma*T2^4);t_ini_:=subs(dat,evalf(subs(T(0)=T2_,T2=T2_,T20=T20_,eqEr_,A[20]=Pi*R^2,A[2]=4*Pi*R^2,dat,%))); |
| (8) |
i.e. tardaría unos 5 minutos en calentarse. Abajo se presenta la evolución temporal de este modelo no lineal, y del modelo linealizado respecto a una Tmedia=(T2_+T20_)/2 poniendo T=Tm+DT y haciendo que DT<<Tm, aunque las desviaciones pueden ser grandes porque no se cumple esto último.
| > | eqBElin:=C*diff(DT(t),t)=E[10]*A[20]-A[2]*sigma*(Tm^4+4*Tm^3*DT(t));eqTm:=Tm=(T2_+T20_)/2;eqBElin_:=evalf(subs(eqTm,A[20]=Pi*R^2,A[2]=4*Pi*R^2,eqEr_,dat,SI0,eqBElin));eqCI:=DT(0)=T2-Tm;eqCI:=DT(0)=subs(eqTm,SI0,T2_-Tm);solLIN:=evalf(dsolve({eqBElin_,eqCI},DT(t))):Tlin:=rhs(eqTm)+rhs(%)*K_;pl_lin:=plot(subs(t=t_s,SI0,Tlin),t_s=0..1e3,T_K=200..400):with(DEtools):pl_nl:=DEplot(eqBE_,T(t),t=0..1e3,T=200..400,[T(0)=T2_/K_],arrows=none):display([pl_lin,pl_nl]); |
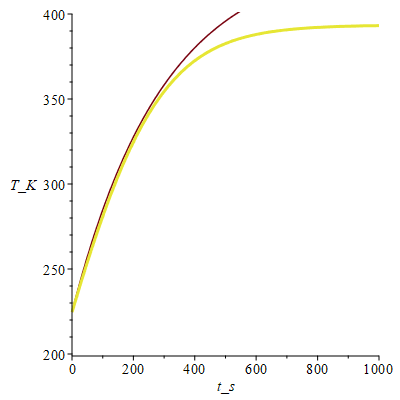 |
donde la curva clara es la no lineal, y la oscura la lineal.
f) Temperaturas estacionarias de disco y esfera, suponiendo para el disco a=0,5 y e=0,9, y para la esfera a=e=0,2.
El recinto considerado es el 11+2+3 (aunque pondremos 1 en vez de 11). Sea A=Pi*R^2. Como T3=2.7 K, tomamos M3bb=sigma*T3^4=0.
| > | eq11:=Q1rad=epsilon1*A*(M1-M1bb)/(1-epsilon1);eq12:=Q1rad=A*F[11,2]*(M2-M1)+A*F[11,3]*(M3bb-M1);eq13:=Q1rad=m1*c1*dT1/dt-alpha*A*E[10]+epsilon1*A*sigma*T1^4;eq21:=Q2rad=epsilon2*4*A*(M2-M2bb)/(1-epsilon2);eq22:=Q2rad=4*A*F[2,11]*(M1-M2)+4*A*F[2,3]*(M3bb-M2);eq23:=Q2rad=m2*c2*dT2/dt; |
| (9) |
cuya solución estacionaria es:
| > | eqs:=evalf(subs(m1=0,m2=0,A=Pi*R^2,eqEr_,eqF11_2,eqF2_11,eqF11_3,eqF2_3,M1bb=sigma*T1^4,M2bb=sigma*T2^4,M3bb=0,dat,SI0,{eq11,eq12,eq13,eq21,eq22,eq23}));sol_:=op(fsolve(eqs,{Q1rad,Q2rad,T1,T2,M1,M2},{T1=100..1000,T2=100..1000}));T1_:=subs(sol_,T1)*K_;T2_:=subs(sol_,T2)*K_;Q1rad_:=subs(sol_,Q1rad)*W_; |
| (10) |
i.e. el disco queda a 405 K y la esfera a 189 K. La interpretación de los términos de los balances energéticos es como sigue:
| > | eq13;subs(dat,evalf(subs(eqEr_,dat,SI0,[Q1rad_,0,-alpha*Pi*R^2*E[10],epsilon1*Pi*R^2*sigma*T1_^4])));eq22;evalf(subs(sol_,M3bb=0,eqF2_11,eqF2_3,A=Pi*R^2,dat,SI0,[Q2rad,4*A*F[2,11]*(M1-M2),4*A*F[2,3]*(M3bb-M2)])); |
| (11) |
i.e. el disco absorbe aEA=34,2 kW del Sol, que en régimen estacionario se compensan con los eAsT4=17,2 kW que salen hacia adelante más los Q1rad=17,0 kW que intercambia hacia atrás. Nótese que, al ser la misma T1, el flujo radiativo hacia adelante y hacia atrás es el mismo, 17,2 kW, así que el flujo que le llega de 2 es 17,2-17,0=0,2 kW, que será suma de la emisión más la reflexión de la esfera.
Por otra parte,
| > | eq12;subs(dat,evalf(subs(sol_,eqF11_2,eqF11_3,dat,SI0,[Q1rad_,Pi*R^2*F[11,2]*(M2-M1),Pi*R^2*F[11,3]*(0-M1)])));eq22;subs(dat,evalf(subs(sol_,eqF2_11,eqF2_3,A=Pi*R^2,dat,SI0,[Q2rad,4*A*F[2,11]*(M1-M2),4*A*F[2,3]*(0-M2)]))); |
| (12) |
i.e. de los 17,0 kW netos hacia atrás, sólo 3,4 kW los intercambia con la esferea, y los otros 13,6 kW van al espacio vacío. El balance de la esfera es sencillo: recibe 3,4 kW netos del disco, y los evacua al espacio vacío casi todos (solo 0,2 kW van a parar al disco).
Puede sorprender que el calor evacuado por la esfera (mejor dicho, la radiación emitida más la reflejada), Q2out=4*A*F23*M2=3,4 kW, se aproxima más a la emisión como cuerpo negro (3,6 kW) que a la emisión como cuerpo gris, que aquí es tan sólo de 0,7 kW. La explicación es sencilla: como el cuerpo 2 sólo está expuesto a radiación IR, su absortancia y su emisividad son iguales (ley de Kirchhoff) y por tanto su temperatura es independiente del valor de epsilon2 (puede comprobarse que se mantiene en 189 K al cambiar epsilon2 de 0,1 a 0,9).
| > | BB_GB:=[4*A*sigma*'T2_'^4,epsilon2*4*A*sigma*'T2_'^4];subs(dat,evalf(subs(A=Pi*R^2,sol_,dat,SI0,%))); |
| (13) |
También se podría haber resuelto aproximadamente el caso de superficies grises analizando separadamente cada cuerpo, despreciando la influencia del 2 en el 1.
| > | eqBE1_:=0=alpha*E[10]*A-epsilon1*A*sigma*T[1]^4-epsilon1*sigma*T[1]^4*A;eqBE2_:=0=epsilon1*epsilon2*sigma*T[1]^4*A*F[2,11]-epsilon2*sigma*T[2]^4*A;T1_:=max(fsolve(simplify(subs(eqEr_,dat,SI0,eqBE1_/A)),T[1]))*K_;T2_:=max(fsolve(simplify(subs(eqF2_11,T[1]=T1_,eqEr_,dat,SI0,eqBE2_/A)),T[2]))*K_; |
| (14) |
obteniéndose los mismos resultados: 404 K para el disco (en vez de 405 K), y 189 K para la esfera.
| > |