| > | restart:#"m13_p50" |
Para un estudio térmico de un apéndice en un satélite geoestacionario, considérese una placa cuadrada de aluminio anodizado (A-7075) de 0,8 m de lado y 2 mm de espesor, mantenida a 300 K, y pintada de negro. El apéndice es un panel en nido de abeja, de 1 cm de espesor, 10 cm de altura y 80 cm de anchura, centrada sobre la placa grande, el cual recibe perpendicularmente los rayos del Sol (ver figura). Este panel está formado por dos láminas de fibra de carbono (CFRP) de 0,5 mm de espesor con acabado en negro, unidas por láminas de aluminio (Al-5052) de 20 m de espesor y 5 mm de anchura de celda. Suponiendo despreciable la conductancia térmica en la unión con la placa grande, se pide:
a) Calcular aproximadamente todos los factores geométricos a partir del valor F12 (factor geométrico desde un lado del panel vertical hacia el lado contiguo de la placa base), determinando el valor de este en el límite de placa base infinita.
b) Calcular los factores geométricos verdaderos (sin la aproximación anterior).
c) Determinar las temperaturas de las caras del panel vertical en estado estacionario, y el valor de cada uno de los términos del balance energético del panel.
d) Resolver ahora suponiendo que la cara iluminada está pintada de blanco.
e) Comparar los resultados anteriores (c y d) con los que se obtendría si no existiese la placa horizontal.
f) Suponiendo que las caras superiores de la placa horizontal se recubren con una manta aislante negra (una MLI pintada de negro), y considerando que sus temperaturas superficiales van a ser diferentes, determinar todas las temperaturas (con la cara iluminada pintada de negro).
g) Repetir el cálculo anterior pero con la cara iluminada pintada de blanco.
h) ¿Y si todas las caras fuesen blancas?
Datos:
| > | with(RealDomain):read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc): |
| > | su:="Al-7075":dat:=[k=140*W_/(m_*K_),Lx=0.8*m_,Ly=0.8*m_,Lxp=0.01*m_,Lzp=0.1*m_,Tinf=2.7*K_,Tb=300*K_,E=1370*W_/m_^2,Lcf=0.5e-3*m_,kcf=1.5*W_/(m_*K_),delta=20e-6*m_,s=5e-3*m_,alpha=0.2,epsilon=0.85];sdat:=get_sol_data(su):dat:=op(dat),Const,SI2,SI1: |
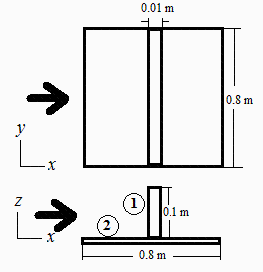
a) Calcular aproximadamente todos los factores geométricos a partir del valor F12 (factor geométrico desde un lado del panel vertical hacia un lado de la placa base), determinando el valor de este en el límite de placa base infinita.
Sea F12 el factor geométrico desde un lado del panel vertical hacia un lado de la placa base. Es fácil ver que F12=1/2 si la placa base fuera infinita, pues, de la radiación emitida por el panel, la mitad irá hacia abajo y la otra mitad hacia arriba, por simetría.
| > | F12_:=0.5;F21=A1*F12/A2;eqA1:=A1=Ly*Lzp;A1_:=subs(dat,rhs(%));eqA2:=A2=Ly*(Lx-Lxp)/2;A2_:=subs(dat,rhs(%));F21_:=subs(F12=F12_,eqA1,eqA2,dat,A1*F12/A2);F13:=1-'F12';F13_:=1-F12_;F23:=1-'F21';F23_:=1-F21_; |
i.e. con la aproximación F12=0,5 y F13=0,5, resulta F21=0,13 y F23=0,87 (i.e. de la energía que emite la placa base hacia arriba, el 13% incide sobre el panel vertical y el 87% se va al espacio).
b) Calcular los factores geométricos verdaderos (sin la aproximación anterior).
De la Tablas (From horizontal rectangle of W·L to adjacent vertical rectangle of H·L, with h=H/L and w=W/L):.

| > | F12:=(1/(Pi*w))*(w*arctan(1/w)+h*arctan(1/h)-sqrt(w^2+h^2)*arctan(1/sqrt(w^2+h^2))+ln(a*b^(w^2)*c^(h^2))/4);a:=(1+w^2)*(1+h^2)/(1+w^2+h^2);b:=w^2*(1+w^2+h^2)/((1+w^2)*(w^2+h^2));c:=h^2*(1+h^2+w^2)/((1+h^2)*(h^2+w^2));plot([seq(F12,w in [0.1,0.5,1,2,10])],h=0..1,F[12]=0..0.5,color=black);eqCheck_w1_h1:=0.200=evalf(subs(w=1,h=1,F12));dat_:=w=(Lx-Lxp)/(2*Ly),h=Lzp/Ly;F21_:=evalf(subs(dat_,dat,F12));F12_:=subs(eqA1,eqA2,dat,A2*F21_/A1);F13:=1-'F12';F13_:=1-F12_; |
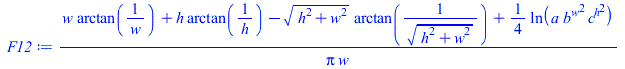 |
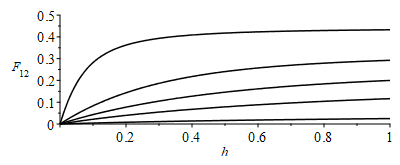 |
i.e. es F21=0,10 en vez de F21=0,13 estimado inicialmente, F12=0,40 (en vez del valor 1/2 del caso infinito). Si en vez de los 0,8 m de envergadura se hubiera tomado el límite infinito, laexpresión analítica es mucho más sencilla, y los nuevos resultados son intermedios: F12=0,40 y F21=0,11.
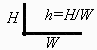
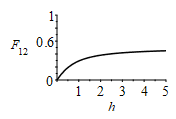
| > | h:='h':F12bid:=(1+h-sqrt(1+h^2))/2;h=H/W;h:=(Lx/2)/Lzp;h_:=subs(dat,%);F12bid_:=subs(h=h_,dat,F12bid);F21bid_:=subs(eqA1,eqA2,dat,A1*F12bid_/A2); |
En resumen, el valor exacto es F12=0,40; con la aproximación bidimensional da F12=0,44, y con el modelo doblemente infinito F12=0,5.
c) Determinar las temperaturas de las caras del panel vertical en estado estacionario, y el valor de cada uno de los términos del balance energético del panel.
Los balances energéticos de cada cara en estado estacionario son (1=cara iluminada, 1p=cara posterior):
| > | F12:='F12':F13:='F13':eqBE:=0=Qin-Qout;eqBE1:=0=E*A1-A1*F12*sigma*(T1^4-T2^4)-A1*F13*sigma*(T1^4-T3^4)-k*A1*(T1-T1p)/Lxp;eqBE1p:=0=k*A1*(T1-T1p)/Lxp-A1*F12*sigma*(T1p^4-T2^4)-A1*F13*sigma*(T1p^4-T3^4);'E'=subs(dat,E);T2_:=subs(dat,Tb);T3_:=subs(dat,Tinf);eqkeff:=keff=k*(8/3)*(delta/s);eqkeff_:=subs(dat,dat,eqkeff);eqkeff__:=keff_=Lxp/(Lcf/kcf+(Lxp-2*Lcf)/keff+Lcf/kcf);keff_:=subs(eqkeff_,dat,rhs(%)); |
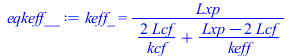 |
i.e. la conductividad efectiva del panel es de 1,49 W/(m·K), y esta último cálculo sirve para comprobar que la resistencia térmica de las láminas de CFRP es despreciable frente a la del núcleo de honeycomb. La expresión de la keff se ha tomado de Heat transfer and thermal radiation modelling.
| > | eqBE1_:=subs(eqA1,eqA2,F12=F12_,F13=F13_,T2=T2_,T3=T3_,k=keff_,dat,SI0,eqBE1);eqBE1p_:=subs(eqA1,eqA2,F12=F12_,F13=F13_,T2=T2_,T3=T3_,k=keff_,dat,SI0,eqBE1p);sol_:=solve({eqBE1_,eqBE1p_},{T1,T1p})[2];T1_:=subs(sol_,T1*K_);'T1_'=TKC(%);T1p_:=subs(sol_,T1p*K_);'T1p_'=TKC(%);eqBE1_terms:=subs(eqA1,eqA2,F12=F12_,F13=F13_,T2=T2_,T3=T3_,k=keff_,dat,SI0,sol_,[E*A1,-A1*F12*sigma*(T1^4-T2^4),-A1*F13*sigma*(T1^4-T3^4),-k*A1*(T1-T1p)/Lxp]);sum_:=convert(eqBE1_terms,`+`);eqBE1p_terms:=subs(eqA1,eqA2,F12=F12_,F13=F13_,T1p=T1p_,T2=T2_,T3=T3_,k=keff_,dat,SI0,sol_,[k*A1*(T1-T1p)/Lxp,-A1*F12*sigma*(T1p^4-T2^4),-A1*F13*sigma*(T1p^4-T3^4)]);sum_:=convert(eqBE1p_terms,`+`) |
i.e. la cara soleada queda a 354 K (81 ºC), recibiendo del Sol 110 W, dándoselos en parte a la base (14 W), al vacío (43 W), y a la otra cara (53 W). Los 53 W que llegan por conducción a la caro opuesta, que queda a 350 K (76 ºC), van en parte a la base (13 W) y al vacío (41 W).
Si no hubiéramos dividido la aleta en dos nodos, sino en uno a T12:
| > | F12:='F12':F13:='F13':F23:='F23':eqBE11p:=E*A1-2*A1*F12*sigma*(T11p^4-T2^4)-2*A1*F13*sigma*(T11p^4-T3^4);T11p_:=solve(subs(eqA1,eqA2,F12=F12_,F13=F13_,T2=Tb,T3=Tinf,dat,SI0,%),T11p)[1]*K_; |
i.e. una T=352 K intermedia entre 354 K y 350 K como era de esperar (y nos ha servido de comprobación del caso de los 2 nodos).
d) Resolver ahora suponiendo que la cara iluminada está pintada de blanco.
| > | eqBE1:=0=alpha*E*A1-epsilon*A1*F12*sigma*(T1^4-T2^4)-epsilon*A1*F13*sigma*(T1^4-T3^4)-k*A1*(T1-T1p)/Lxp;eqBE1p:=0=k*A1*(T1-T1p)/Lxp-A1*F12*sigma*(T1p^4-T2^4)-A1*F13*sigma*(T1p^4-T3^4);eqBE1_:=subs(eqA1,eqA2,F12=F12_,F13=F13_,T2=T2_,T3=T3_,k=keff_,dat,SI0,eqBE1);eqBE1p_:=subs(eqA1,eqA2,F12=F12_,F13=F13_,T2=T2_,T3=T3_,k=keff_,dat,SI0,eqBE1p);sol_:=solve({eqBE1_,eqBE1p_},{T1,T1p})[2];T1_:=subs(sol_,T1*K_);'T1_'=TKC(%);T1p_:=subs(sol_,T1p*K_);'T1p_'=TKC(%);eqBE1_terms:=subs(eqA1,eqA2,F12=F12_,F13=F13_,T2=T2_,T3=T3_,k=keff_,dat,SI0,sol_,[alpha*E*A1,-epsilon*A1*F12*sigma*(T1^4-T2^4),-epsilon*A1*F13*sigma*(T1^4-T3^4),-k*A1*(T1-T1p)/Lxp]);sum_:=convert(eqBE1_terms,`+`);eqBE1p_terms:=subs(eqA1,eqA2,F12=F12_,F13=F13_,T2=T2_,T3=T3_,k=keff_,dat,SI0,sol_,[k*A1*(T1-T1p)/Lxp,-A1*F12*sigma*(T1p^4-T2^4),-A1*F13*sigma*(T1p^4-T3^4)]);sum_:=convert(eqBE1p_terms,`+`); |
i.e. la cara 1 queda ahora a 277 K (en vez de a 354 K), recibiendo del Sol 22 W y otros 3 W de la placa de abajo, y de estos 25 W pasan 12 W por conducción a la capa posterior y casi 14 W salen por radiación al espacio, mientras que la cara 1’ recibe los 12 W de la 1 más 4 W de la 2’, y emite los 16 W al espacio, quedando a 276 K (en vez de a 350 K).
Como antes, podemos comparar este modelo de dos nodos con el de un nodo (conjunto del 1 y el 1p):
| > | eqBE11p:=alpha*E*A1-(epsilon+1)*A1*F12*sigma*(T11p^4-T2^4)-(epsilon+1)*A1*F13*sigma*(T11p^4-T3^4);T11p_:=solve(subs(eqA1,eqA2,F12=F12_,F13=F13_,T2=Tb,T3=Tinf,dat,SI0,%),T11p)[1]*K_; |
i.e., si se considera toda la aleta a la misma temperatura, quedaría a 277 K si la cara frontal es blanca y la posterior negra.
e) Comparar los resultados anteriores (c y d) con los que se obtendría si no existiese la placa horizontal.
Bastaría poner T2=T2'=T3 (2.7 K) en los balances anteriores, pero los reescribiremos. Siguiendo con la cara pintada de blanco:
| > | eqBE1:=0=alpha*E*A1-epsilon*A1*sigma*(T1^4-T3^4)-k*A1*(T1-T1p)/Lxp;eqBE1p:=0=k*A1*(T1-T1p)/Lxp-A1*sigma*(T1p^4-T3^4);eqBE1_:=subs(eqA1,eqA2,T3=T3_,k=keff_,dat,SI0,eqBE1);eqBE1p_:=subs(eqA1,eqA2,T3=T3_,k=keff_,dat,SI0,eqBE1p);sol_:=solve({eqBE1_,eqBE1p_},{T1,T1p})[2];T1_:=subs(sol_,T1*K_);'T1_'=TKC(%);T1p_:=subs(sol_,T1p*K_);'T1p_'=TKC(%);eqBE1_terms:=subs(eqA1,eqA2,T3=T3_,k=keff_,dat,SI0,sol_,[alpha*E*A1,-epsilon*A1*sigma*(T1^4-T3^4),-k*A1*(T1-T1p)/Lxp]);sum_:=convert(eqBE1_terms,`+`);eqBE1p_terms:=subs(eqA1,eqA2,T3=T3_,k=keff_,dat,SI0,sol_,[k*A1*(T1-T1p)/Lxp,-A1*sigma*(T1p^4-T3^4)]);sum_:=convert(eqBE1p_terms,`+`); |
i.e. T1=227 K, T1’=226 K, la cara 1 absorbe 22 W, emite 10 W y pasa 12 W al nodo 1’, que los emite al vacío. Vemos la importancia de tener la placa base a 300 K para mantener caliente la aleta. Puede comprobarse con el model de un solo nodo:
| > | eqBE11p:=0=alpha*E*A1-(epsilon+1)*A1*sigma*(T11p^4-T3^4);T11p_:=solve(subs(eqA1,eqA2,F12=F12_,F13=F13_,T2=Tb,T3=Tinf,dat,SI0,%),T11p)[1]*K_; |
Si la cara iluminada también fuese cuerpo negro el resultado para un nodo es sencillísimo: T=(E/(2sigma)^(1/4)=331,5 K (58 ºC).
f) Suponiendo que las caras superiores de la placa horizontal se recubren con una manta aislante negra (una MLI pintada de negro), y considerando que sus temperaturas superficiales van a ser diferentes, determinar todas las temperaturas (con la cara iluminada pintada de negro.
Ahora la temperatura de la placa base vendrá dada por su balance energético (ya no está regulada a 300 K).
El modelo más sencillo es el de dos nodos: nodo 11p (toda la aleta) y nodo 22p (toda la placa). Si todos son cuerpos negros
| > | eqBE11p:=0=E*A1-2*A1*F12*sigma*(T11p^4-T22p^4)-2*A1*F13*sigma*(T11p^4-T3^4);eqBE22p:=0=2*A1*F12*sigma*(T11p^4-T22p^4)-2*A2*F23*sigma*(T22p^4-T3^4);sol_:=fsolve(subs(eqA1,eqA2,F12=F12_,F13=F13_,F23=F23_,T2=T2_,T3=T3_,dat,SI0,{eqBE11p,eqBE22p}),{T11p,T22p},T22p=100..400); |
i.e. si la cara iluminada fuese cuerpo negro, la aleta quedaría a 335 K y la placa base a 190 K.
No cuesta trabajo ver qué pasaría si la cara iluminada fuese blanca, tomando alpha=0,2 (y rho=1-alpha=0,8), pero manteniendo epsilon=1 para considerar cuerpos negros en el IR.
| > | eqBE11p:=0=alpha*E*A1-2*A1*F12*sigma*(T11p^4-T22p^4)-2*A1*F13*sigma*(T11p^4-T3^4);eqBE22p:=0=(1-alpha)*E*A1*F12+2*A1*F12*sigma*(T11p^4-T22p^4)-2*A2*F23*sigma*(T22p^4-T3^4);sol_:=fsolve(subs(eqA1,eqA2,F12=F12_,F13=F13_,F23=F23_,T2=T2_,T3=T3_,dat,SI0,{eqBE11p,eqBE22p}),{T11p,T22p},T22p=100..400); |
i.e. con la cara blanca, la aleta quedaría a 233 K y la placa base a 190 K, mientras que si la cara iluminada fuese también cuerpo negro, la aleta quedaría a 335 K y la placa base a 190 K. La cara 2 no refleja en la banda solar porque es cuerpo negro.
Es curioso ver que la placa base queda a la misma temperatura tanto si la cara iluminada es blanca como si es negra; la explicación es que lo que recibe por reflexión solar compensa exactamente la merma en la banda infrarroja.
Si consideramos las 4 caras por separado, y suponemos que no hay conexión térmica en el encastre entre aleta y placa, ni entre las partes delantera y trasera de la placa base, las ecuaciones nodales serían:
| > | eqBE1:=0=E*A1-A1*F12*sigma*(T1^4-T2i^4)-A1*F13*sigma*(T1^4-T3^4)-k*A1*(T1-T1p)/Lxp;eqBE1p:=0=k*A1*(T1-T1p)/Lxp-A1*F12*sigma*(T1p^4-T2p^4)-A1*F13*sigma*(T1p^4-T3^4);eqBE2:=0=A1*F12*sigma*(T1^4-T2i^4)-A2*F23*sigma*(T2i^4-T3^4);eqBE2p:=0=A1*F12*sigma*(T1p^4-T2p^4)-A2*F23*sigma*(T2p^4-T3^4);sol_:=fsolve(subs(eqA1,eqA2,F12=F12_,F13=F13_,F23=F23_,T2=T2_,T3=T3_,k=keff_,dat,SI0,[eqBE1,eqBE1p,eqBE2,eqBE2p]),{T1,T1p,T2i,T2p},{T1=100..400,T1p=100..400,T2i=10..400,T2p=10..400}); |
i.e. con este modelo de 4 nodos, con la cara frontal negra hay algo más de diferencia: la aleta alcanza 337,3 K por delante y 332,8 K por detrás (frente a los 335 K de media anterior), y la placa base alcanzaría 191,6 K por delante y 189,1 K por detrás (frente a los 190,3 K de media anterior).
g) Repetir el cálculo anterior pero con la cara iluminada pintada de blanco.
Con el modelo de 4 nodos con la cara iluminada blanca (alpha=0,2 y rho=0,8), pero manteniendo epsilon=1.
| > | eqBE1:=0=alpha*E*A1-A1*F12*sigma*(T1^4-T2i^4)-A1*F13*sigma*(T1^4-T3^4)-k*A1*(T1-T1p)/Lxp;eqBE1p:=0=k*A1*(T1-T1p)/Lxp-A1*F12*sigma*(T1p^4-T2p^4)-A1*F13*sigma*(T1p^4-T3^4);eqBE2:=0=(1-alpha)*E*A1*F12+A1*F12*sigma*(T1^4-T2i^4)-A2*F23*sigma*(T2i^4-T3^4);eqBE2p:=0=A1*F12*sigma*(T1p^4-T2p^4)-A2*F23*sigma*(T2p^4-T3^4);sol_:=fsolve(subs(eqA1,eqA2,F12=F12_,F13=F13_,F23=F23_,T2=T2_,T3=T3_,k=keff_,dat,SI0,[eqBE1,eqBE1p,eqBE2,eqBE2p]),{T1,T1p,T2i,T2p},{T1=100..400,T1p=100..400,T2i=10..400,T2p=10..400}); |
i.e. con la cara frontal blanca, la aleta alcanza 233,4 K por delante y 232,4 K por detrás (frente a los 233 K de media anterior), y la placa base alcanzaría 219 K por delante y 132 K por detrás (frente a los 190 K de media anterior).
Pero si para la cara blanca retenemos epsilon<1, habría que recurrir al método de las exitancias, aunque una aproximación podría ser:
| > | eqBE1:=0=alpha*E*A1-epsilon*A1*F12*sigma*(T1^4-T2i^4)-epsilon*A1*F13*sigma*(T1^4-T3^4)-k*A1*(T1-T1p)/Lxp;eqBE1p:=0=k*A1*(T1-T1p)/Lxp-A1*F12*sigma*(T1p^4-T2p^4)-A1*F13*sigma*(T1p^4-T3^4);eqBE2:=0=(1-alpha)*E*A1*F12+epsilon*A1*F12*sigma*(T1^4-T2i^4)-A2*F23*sigma*(T2i^4-T3^4);eqBE2p:=0=A1*F12*sigma*(T1p^4-T2p^4)-A2*F23*sigma*(T2p^4-T3^4);sol_:=fsolve(subs(eqA1,eqA2,F12=F12_,F13=F13_,F23=F23_,T2=T2_,T3=T3_,k=keff_,dat,SI0,[eqBE1,eqBE1p,eqBE2,eqBE2p]),{T1,T1p,T2i,T2p},{T1=100..400,T1p=100..400,T2i=10..400,T2p=10..400}); |
i.e. T1=237 K (en vez de 233 K; no se enfría tanto porque emite menos), T1p=237 K (en vez de 232 K), T2=220 K (en vez de 219 K), y T2p=134 K (en vez de 132 K).
Los términos de los balances valen:
| > | eqBE1_terms:=subs(eqA1,eqA2,F12=F12_,F13=F13_,T3=T3_,k=keff_,dat,SI0,sol_,[alpha*E*A1,-epsilon*A1*F12*sigma*(T1^4-T2i^4),-epsilon*A1*F13*sigma*(T1^4-T3^4),-k*A1*(T1-T1p)/Lxp]);sum_:=convert(eqBE1_terms,`+`);eqBE1p_terms:=subs(eqA1,eqA2,F12=F12_,F13=F13_,T3=T3_,k=keff_,dat,SI0,sol_,[k*A1*(T1-T1p)/Lxp,-A1*F12*sigma*(T1p^4-T2p^4),-A1*F13*sigma*(T1p^4-T3^4)]);sum_:=convert(eqBE1p_terms,`+`);eqBE2_terms:=subs(eqA1,eqA2,F12=F12_,F13=F13_,F23=F23_,T3=T3_,k=keff_,rho=1-alpha,dat,SI0,sol_,[epsilon*A1*F12*sigma*(T1^4-T2i^4),A1*F12*rho*E,-A2*F23*sigma*(T2i^4-T3^4)]);sum_:=convert(eqBE2_terms,`+`);eqBE2p_terms:=subs(eqA1,eqA2,F12=F12_,F13=F13_,F23=F23_,T3=T3_,k=keff_,dat,SI0,sol_,[A1*F12*sigma*(T1p^4-T2p^4),-A2*F23*sigma*(T2p^4-T3^4)]);sum_:=convert(eqBE2p_terms,`+`); |
e.g. la eqBE1_terms enseña que la cara iluminada absorbe 22 W del sol, que en régimen estacionario salen en parte (1.3 W) hacia abajo a la superficie 2, otra parte por conducción hacia atrás (7,3 W), y el resto (13,4 W) hacia el espacio de fiondo (arriba y delante).
h) ¿Y si todas las caras fuesen blancas?
Habría que usar el método de las exitancias. Para los 4 nodos tendremos 8 ecuaciones con 8 incógnitas (M1,T1,M1p,T1p,M2,T2,M2p,T2p).
ADICIONAL.
Resolución. Los términos en la banda visible los añadimos explícitamente, y sólo consideramos la absorción directa en 1 (aEA), la absorción solar en 2 debido a lo que refleja 1 (arEAF12), y la absorción solar en 1 debido a lo que refleja 2 de lo que le llega (arrEAF12F21), despreciando retrorreflexiones ulteriores (la siguiente sería una absorción en 2 igual a arrrEAF12F21F12).
Nodo 1:
| > | eq1:=(epsilon1*A1/(1-epsilon1))*(M1-M1bb)=-alpha1*E*A1-alpha1*rho2*rho1*E*A1*F12*F21+k*A1*(T1-T1p)/Lxp;eq2:=A1*F12*(M2-M1)+A1*F13*(M3-M1)=-alpha1*E*A1+k*A1*(T1-T1p)/Lxp; |
Nodo 2:
| > | eq3:=(epsilon2*A2/(1-epsilon2))*(M2-M2bb)=-alpha2*rho1*E*A1*F12;eq4:=A2*F21*(M1-M2)+A2*F23*(M3-M2)=-alpha2*rho1*E*A1*F12; |
Nodo 1p:
| > | eq5:=(epsilon1*A1/(1-epsilon1))*(M1p-M1pbb)=-k*A1*(T1-T1p)/Lxp;eq6:=A1*F12*(M2p-M1p)+A1*F13*(M3-M1p)=-k*A1*(T1-T1p)/Lxp; |
Nodo 2p:
| > | eq7:=(epsilon2*A2/(1-epsilon2))*(M2p-M2pbb)=0;eq8:=A2*F21*(M1p-M2p)+A2*F23*(M3-M2p)=0; |
Vemos que de la ecuación eq7 se deduce que el nodo 2p se comporta como cuerpo negro (M2p=M2pbb).
Caso con todas las superficies blancas (ww means whiteSOL_whiteIR).
| > | datww:=alpha1=0.2,epsilon1=0.85,rho1=0.8,alpha2=0.2,epsilon2=0.85,rho2=0.8,k=keff_,A1=A1_,A2=A2_,F12=F12_,F13=F13_,F23=F23_,F21=F21_,M1bb=sigma*T1^4,M2bb=sigma*T2^4,M1pbb=sigma*T1p^4,M2pbb=sigma*T2p^4,M3=0; |
| > | eq1_:=subs(datww,dat,SI0,eq1);eq2_:=subs(datww,dat,SI0,eq2);eq3_:=subs(datww,dat,SI0,eq3);eq4_:=subs(datww,dat,SI0,eq4);eq5_:=subs(datww,dat,SI0,eq5);eq6_:=subs(datww,dat,SI0,eq6);eq7_:=subs(datww,dat,SI0,eq7);eq8_:=subs(datww,dat,SI0,eq8);sol_:=fsolve({eq1_,eq2_,eq3_,eq4_,eq5_,eq6_,eq7_,eq8_},{M1,T1,M1p,T1p,M2,T2,M2p,T2p},{T1=200..300,T2p=100..300});T1_T1p_T2_T2p_:=subs(sol_,[T1,T1p,T2,T2p]); |
i.e. con las 4 superficies blancas, quedaría T1=235 K, T1p=234 K, T2=165 K y T2p=128 K. Estos valores son similares a cuando solo era blanca la aleta. Vamos a calcular las absorciones solares:
| > | aEA_A1:=alpha1*E;aEA_A1_:=subs(datww,dat,%);arEAF12_A2:=alpha2*rho1*E*A1*F12/A2;arEAF12_A2_:=subs(datww,dat,%);arrEAF12F21_A1:=alpha1*rho2*rho1*E*A1/A2;arrEAF12F21_A1_:=subs(datww,dat,%);arrEAF12F21F12_A2:=alpha2*rho1*rho2*E*A1*F12*F21*F12/A2;arrEAF12F21F12_A2_:=subs(datww,dat,%); |
i.e. en la 1ª incidencia la cara 1 (blanca) absorbe 274 W/m2 (22 W, reflejándose los otros 88 W de los 110 W de incidencia); en la 1ª reflexión la cara 2 absorbe 22 W/m2 (7 W de los 88 reflejados); la retrorreflexión de 2 a 1 hace que la cara 1 absorba 44 W/m2 (3,55 W; y ya no hemos incluido más; el siguiente sería la segunda absorción solar en 2, que vemos que es de 0,7 W/m2 ( 0,23 W).
Podemos resolver ahora también el caso de cara 1 blanca y las demás negras, que ya resolvimos aproximadamente en el apartado g)..
| > | datw:=alpha1=0.2,epsilon1=0.85,rho1=0.8,alpha2=1,epsilon2=0.999,rho2=0,k=keff_,A1=A1_,A2=A2_,F12=F12_,F13=F13_,F23=F23_,F21=F21_,M1bb=sigma*T1^4,M2bb=sigma*T2^4,M1pbb=sigma*T1p^4,M2pbb=sigma*T2p^4,M3=0;eq1_:=subs(datw,dat,SI0,eq1);eq2_:=subs(datw,dat,SI0,eq2);eq3_:=subs(datw,dat,SI0,eq3);eq4_:=subs(datw,dat,SI0,eq4);eq5_:=subs(datw,dat,SI0,eq5);eq6_:=subs(datw,dat,SI0,eq6);eq7_:=subs(datw,dat,SI0,eq7);eq8_:=subs(datw,dat,SI0,eq8);sol_:=fsolve({eq1_,eq2_,eq3_,eq4_,eq5_,eq6_,eq7_,eq8_},{M1,T1,M1p,T1p,M2,T2,M2p,T2p}, {T1=200..300,T2p=100..300});T1_T1p_T2_T2p_:=subs(sol_,[T1,T1p,T2,T2p]); |
i.e. la cara iluminada queda a 241 K en vez de a los 237 K calculados en el apartado g).
Para comprobar, podemos resolver el caso de todas superficies cuerpos negros.
| > | datw:=alpha1=1,epsilon1=0.999,rho1=0,alpha2=1,epsilon2=0.999,rho2=0,k=keff_,A1=A1_,A2=A2_,F12=F12_,F13=F13_,F23=F23_,F21=F21_,M1bb=sigma*T1^4,M2bb=sigma*T2^4,M1pbb=sigma*T1p^4,M2pbb=sigma*T2p^4,M3=0;eq1_:=subs(datw,dat,SI0,eq1);eq2_:=subs(datw,dat,SI0,eq2);eq3_:=subs(datw,dat,SI0,eq3);eq4_:=subs(datw,dat,SI0,eq4);eq5_:=subs(datw,dat,SI0,eq5);eq6_:=subs(datw,dat,SI0,eq6);eq7_:=subs(datw,dat,SI0,eq7);eq8_:=subs(datw,dat,SI0,eq8);sol_:=fsolve({eq1_,eq2_,eq3_,eq4_,eq5_,eq6_,eq7_,eq8_},{M1,T1,M1p,T1p,M2,T2,M2p,T2p}, {T1=200..400,T2p=100..300});T1_T1p_T2_T2p_:=subs(sol_,[T1,T1p,T2,T2p]); |
que coincide con el cálculo anteriormente hecho con el modelo de cuerpos negros.
| > |