| > | restart:#"m13_p48" |
Para un estudio térmico preliminar de un apéndice en un satélite geoestacionario se va a considerar una cáscara semiesférica de 25 cm de diámetro y 1 mm de espesor de aluminio anodizado, recubierta exteriormente por una capa de kapton muy delgada, y cerrada en su plano diametral por un panel de nido de abeja de 1 cm de espesor y conductividad térmica de 0,1 W/(m•K) (se supondrá isotrópica), recubierto por ambas caras con 1 mm de espesor de aluminio anodizado, y de cuyo centro sale un soporte telescópico que lo une al cuerpo del satélite. La lámina externa del panel está pintada de negro y hace buen contacto térmico con la cáscara, mientras que la interior no llega a hacer contacto. Se va a suponer despreciable la influencia del cuerpo del satélite y del mástil de unión, y régimen estacionario. Se pide:
a) Recopilar los valores que se van a usar para las propiedades térmicas y radiativas, indicando la incertidumbre estimada.
b)Suponiendo que la transmisión de calor por el interior fuese tan efectiva que todo el conjunto fuese isotermo), determinar la temperatura del conjunto en función de la inclinación solar () respecto al eje común, Tsp(), en los casos extremos.
c) Suponiendo que sea suficiente considerar tres superficies isotermas, la cáscara semiesférica (a Ts), la cara externa del panel (a Tpe), y la cara interna del panel (a Tpi), establecer los balances energéticos separados de cada nodo y las temperaturas extremas.
Datos:
| > | with(RealDomain):read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc): |
| > | su:="Aluminio_anodizado":dat:=[D=0.25*m_,ds=1e-3*m_,alpha[a]=0.2,epsilon[a]=0.6,alpha[k]=0.4,epsilon[k]=0.8,alpha[b]=0.95,epsilon[b]=0.90,dp=1e-2*m_,kp=0.1*W_/(m_*K_),Tinf=2.73*K_,E=1370*W_/m_^2]; |
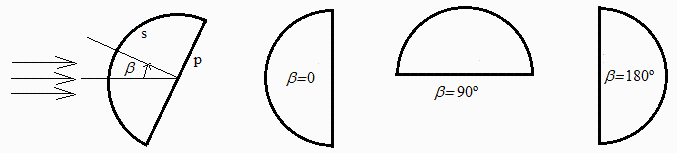
Superficies: k=kapton, b=black, a=aluminium(anodised).
| > | sdat:=get_sol_data(su):dat:=op(dat),Const,SI2,SI1: |
a) Recopilar los valores que se van a usar para las propiedades térmicas y radiativas, indicando la incertidumbre estimada.
Como solo interesa el régimen estacionario, no hay que tener en cuenta propiedades de inercia térmica.
No se considera la situación de eclipse (no parece consistente con el modelo estacionario, aunque un eclipse en GEO puede durar hasta 70 min).
Se van a tomar los siguientes datos:
Aluminio anodizado:
k=200 W/(m·K); depende del tipo de aleación, puede variar entre 120 y 220.
alpha=0.2; depende mucho del grado y tipo de anodizado, puede variar entre 0.1 y 0.9.
epsilon=0.6; depende mucho del grado y tipo de anodizado, puede variar entre 0.4 y 0.9 (y el aluminio pulido puede llegar a 0,05).
Supondremos además que la resistencia térmica de contacto en la unión entre la semiesfera y la placa exterior es nula, pero un valor del orden de 1 K/W sería más apropriado.
kapton:
k=0.12 W/(m·K); puede variar entre 0.10 y 0.15. Suponemos que el recubrimiento es tan fio que es isotermo.
alpha=0.40; puede variar entre 0.3 y 0.5 (crece con el espesor).
epsilon=0.80; puede variar entre 0.4 y 0.9 (crece con el espesor).
panel de nido de abeja:
k=0,1 W/(m·K) es dato; la conductividad efectiva no será isotrópica; si la media es 0,1, puede haber direcciones con 0,05 W/(m·K) y otras con 0,15 W/(m·K).
pintura negra:
alpha=0.95; puede variar entre 0.9 y 0.98.
epsilon=0.90; puede variar entre 0.85 y 0.95.
para GEO tomamos el estándar E=1370 W/m2, pero la irradiancia solar varía entre 1315 (a primeros de julio) y 1425 (a primeros de enero), por la elipticidad de la órbita de la Tierra alrededor del Sol, +/-1 W/m2 por los ciclos de las manchas solares, y unos +/- 10 W/m2 de fluctuación esporádica por variación de las manchas solares.
Tinf=2,73+/-0,05 K, pero lo vamos a despreciar porque no esperamos temperaturas de <100 K.
b)Suponiendo que la transmisión de calor por el interior fuese tan efectiva que todo el conjunto fuese isotermo), determinar la temperatura del conjunto en función de la inclinación solar () respecto al eje común, Tsp(), en los casos extremos.
Parece claro que el caso más caliente será cuando incidan los rayos del Sol perpendicularmente a la cara negra, por su máxima absorción (en realidad sería con una pequeña inclinación para salvar la sombra del cuerpo del satélite). El caso más frío será cuando el Sol le dé de perfil, pues el área proyectada es mínima).
Conviene separar en 2 casos:
Caso 1 (0<beta<Pi/2), irradiación por delante, sólo sobre la semiesfera, de área frontal Af1=Afs.
Caso 2 (Pi/2<beta<Pi), irradiación por detrás, sobre la base y la semiesfera, de área frontal total Af2=Afs+Afp.
| > | Afs_:=(Pi*D^2/4)*(1+cos(beta))/2;Af1_:='Afs_';Afp_:=-(Pi*D^2/4)*cos(beta);Af2_:='Afs_+Afp_';Af_:=piecewise(beta<Pi/2,Af1_,Af2_);plot(subs(D=1,[Afs_,Afp_,Af_]),beta=0..Pi,Af_D2=0..1); |
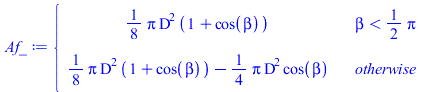 |
|
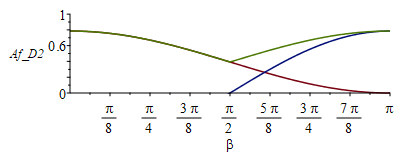 |
i.e. entre 0<beta<Pi/2 vale Afs_=Pi*R^2*(1+cos(beta))/2 (curva roja) y Afp_=0 (queda oculto detrás), mientras que entre Pi/2<beta<Pi vale Afs_=Pi*R^2*(1+cos(beta))/2 (curva roja), más Afp_=-Pi*R^2*cos(beta) (curva verde, que sumadas dan la curva amarilla).
Sea eqBEs el balance energético cuando solo se ilumina la esfera, y eqBEsp cuando también se ilumina el plano.
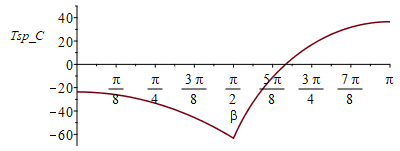
| > | eqBE:=DE=W+Q;eqBE:=Qin=Qout;eqBE1:=alpha[k]*E*Af1=epsilon[k]*2*(Pi*D^2/4)*sigma*(Tsp^4-Tinf^4)+epsilon[b]*(Pi*D^2/4)*sigma*(Tsp^4-Tinf^4);eqBE2:=alpha[k]*E*Afs+alpha[b]*E*Afp=epsilon[k]*2*(Pi*D^2/4)*sigma*(Tsp^4-Tinf^4)+epsilon[b]*(Pi*D^2/4)*sigma*(Tsp^4-Tinf^4);Tsp1:=solve(subs(Af1=Af1_,Afs=Afs_,Afp=Afp_,dat,SI0,eqBE1),Tsp)[1];Tsp2:=solve(subs(Af1=Af1_,Afs=Afs_,Afp=Afp_,dat,SI0,eqBE2),Tsp)[1];Tsp_t:=piecewise(beta<Pi/2,Tsp1,Tsp2);plot(Tsp_t-273,beta=0..Pi,Tsp_C=-70..50);Tsp0:=evalf(subs(beta=0,Tsp_t))*K_;Tsp0:=TKC(%);Tsp90:=evalf(subs(beta=Pi/2,Tsp_t))*K_;Tsp90:=TKC(%);Tsp180:=evalf(subs(beta=Pi,Tsp_t))*K_;Tsp180:=TKC(%); |
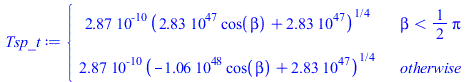 |
|
 |
|
| (1) |
i.e. con el modelo isotermo global, la temperatura de equilibrio sería de 249 K para beta=0, 210 K para beta=90º, y 310 K para beta=180º.
c) Suponiendo que sea suficiente considerar tres superficies isotermas, la cáscara semiesférica (a Ts), la cara externa del panel (a Tpe), y la cara interna del panel (a Tpi), establecer los balances energéticos separados de cada nodo y las temperaturas extremas.
Ahora cada caso consta de tres sistemas (s=semiesfera , pe=panel_externo y pi=panel_interno).
Caso 1: 0<beta<Pi/2.
BEs. La cáscara absorbe parte de la radiación solar, radia en el IR por ambas caras, y conduce a la lámina plana externa (se desprecia el resto).
Para Qrspe se usa el modelo más general de recinto de dos nodos. Para Qkspe se toma como distancia característica D.
BEpi. La placa interior recibe calor IR de la cáscara, y conduce a través del panel.
EBpe. La placa exterior recibe calor por el borde de la cáscara y por el panel, y emite por la cara externa.
| > | eqBE1s:=alpha[k]*E*Af1=epsilon[k]*2*(Pi*D^2/4)*sigma*(Ts^4-Tinf^4)+Qrspi+k*Pi*D*ds*(Ts-Tpe)/D;Qrspi_:=sigma*(Ts^4-Tpi^4)/((1-epsilon[1])/(A[1]*epsilon[1])+1/(A[1]*Fsp)+(1-epsilon[2])/(A[2]*epsilon[2]));Qrspi_:=(Pi*D^2/4)*sigma*(Ts^4-Tpi^4)/((1-epsilon[a])/(2*epsilon[a])+1/(2*Fsp)+(1-epsilon[a])/(1*epsilon[a]));eqBE1pi:=Qrspi=kp*(Pi*D^2/4)*(Tpi-Tpe)/dp;eqBE1pe:=k*Pi*D*ds*(Ts-Tpe)/D+kp*(Pi*D^2/4)*(Tpi-Tpe)/dp=epsilon[b]*(Pi*D^2/4)*sigma*(Tpe^4-Tinf^4);eqFsp:=Fsp=1/2;eqs1:=evalf(subs(Qrspi=Qrspi_,Af1=Af1_,Afs=Afs_,Afp=Afp_,eqFsp,dat,sdat,SI0,[eqBE1s,eqBE1pi,eqBE1pe])); |
![`/`(`*`(sigma, `*`(`+`(`-`(`*`(`^`(Tpi, 4))), `*`(`^`(Ts, 4))))), `*`(`+`(`/`(`*`(`+`(1, `-`(epsilon[1]))), `*`(A[1], `*`(epsilon[1]))), `/`(1, `*`(A[1], `*`(Fsp))), `/`(`*`(`+`(1, `-`(epsilon[2]))), ...](images/p481_24.gif) |
|
![`+`(`/`(`*`(`/`(1, 4), `*`(Pi, `*`(`^`(D, 2), `*`(sigma, `*`(`+`(`-`(`*`(`^`(Tpi, 4))), `*`(`^`(Ts, 4)))))))), `*`(`+`(`/`(`*`(`/`(3, 2), `*`(`+`(1, `-`(epsilon[a])))), `*`(epsilon[a])), `/`(`*`(`/`(1...](images/p481_25.gif) |
|
| (2) |
Caso 2: beta>Pi/2.
BEs. La cáscara absorbe parte de la radiación solar que le llega (vale la ecuación del caso 1).
BEpi. La placa interior sigue con los mismos acoplamientos (vale la ecuación del caso 1).
EBpe. La placa exterior absorbe parte de la radiación solar que le llega, más los acoplamientos el caso 1.
| > | eqBE2s:='eqBE1s';eqBE2pi:='eqBE1pi';eqBE2pe:=alpha[b]*E*Afp_+k*Pi*D*ds*(Ts-Tpe)/D+kp*(Pi*D^2/4)*(Tpi-Tpe)/dp=epsilon[b]*(Pi*D^2/4)*sigma*(Tpe^4-Tinf^4);eqs2:=evalf(subs(Qrspi=Qrspi_,Af1=Af1_,Afs=Afs_,Afp=Afp_,eqFsp,dat,sdat,SI0,[eqBE2s,eqBE2pi,eqBE2pe])); |
| (3) |
Otra vez parece que el caso más caliente será el de beta=180º, y el más frío el de beta=90º, pero vamos a representar las 3 temperaturas [ºC] en función del ángulo [rad].
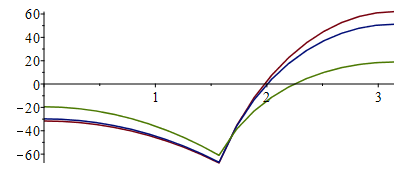
| > | N:=20:for i from 0 to N do b[i]:=Pi*(i/N);if is(i<N/2) then sol:=fsolve(subs(beta=b[i],eqs1),{Ts,Tpi,Tpe},{Ts=10..400,Tpi=10..400,Tpe=10..400}); else sol:=fsolve(subs(beta=b[i],eqs2),{Ts,Tpi,Tpe},{Ts=10..400,Tpi=10..400,Tpe=10..400});end if;Ts_[i]:=[b[i],subs(sol,Ts-273)];Tpi_[i]:=[b[i],subs(sol,Tpi-273)];Tpe_[i]:=[b[i],subs(sol,Tpe-273)];od:plot({[seq(Ts_[i],i=0..N)],[seq(Tpi_[i],i=0..N)],[seq(Tpe_[i],i=0..N)]});Ts0:=op(2,Ts_[0])*'ºC';Tpi0:=op(2,Tpi_[0])*'ºC';Tpe0:=op(2,Tpe_[0])*'ºC';Ts90:=op(2,Ts_[N/2])*'ºC';Tpi90:=op(2,Tpi_[N/2])*'ºC';Tpe90:=op(2,Tpe_[N/2])*'ºC';Ts180:=op(2,Ts_[N])*'ºC';Tpi180:=op(2,Tpi_[N])*'ºC';Tpe180:=op(2,Tpe_[N])*'ºC'; |
 |
|
| (4) |
i.e. el caso más caliente es para beta=180º, con Ts=19 ºC, Tpi=51 ºC, y Tpe=62 ºC, y el caso más frío es para beta=90º, con Ts=-61 ºC, Tpi=-67 ºC, Tpe=-68 ºC).
Para beta=0º: Ts=-20 ºC, Tpi=-30 ºC, Tpe=-32 ºC).
| > |