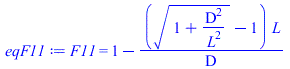
>	restart:#"m13_p42"

Se quiere estudiar el enfriamiento al aire de un manguito de acero inoxidable de 1 mm de espesor, 10 cm de diámetro y 10 cm de longitud, recién sacado de un horno a 1000 K. Suponiendo un coeficiente de convección natural de 10 W/(m2•K) tanto para la cara externa como para la interna, un factor geométrico de la superficie interior con ella misma dado por  , siendo d=D/L, y que tanto el aire como el recinto donde tiene lugar el proceso están a 25 ºC, se pide:

a) Plantear el balance energético del manguito, en un instante genérico, en función de su temperatura.

b) Determinar el valor de los siguientes factores geométricos: el mencionado en este caso y en los casos límite de longitud muy pequeña o muy grande (para diámetro fijo); el factor geométrico entre la superficie interior y una de las bases (aberturas); el factor geométrico entre las bases (aberturas).

c) Determinar los valores de los flujos de calor por convección y radiación en el instante inicial, suponiendo cuerpo negro.

d) Determinar la velocidad inicial de enfriamiento en el caso anterior.

e) Volver a resolver el problema para el caso de acabado metálico no pintado.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):read`../therm_eq.m`:

>	su1:="Aire":su2:="Acero_inox":dat:=[delta=1e-3*m_,D=0.1*m_,L=0.1*m_,T1=1000*K_,h=10*W_/(m_^2*K_),T0=(25+273.15)*K_];eqF11:=F11=1-(sqrt(1+(D/L)^2)-1)/(D/L);

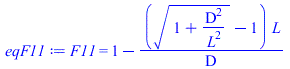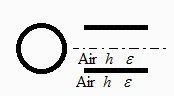
>	Sdat:=get_sol_data(su2);dat:=op(dat),get_gas_data(su1),Const,SI2,SI1:Metal_IR_absorptance:=epsilon=subs(Sdat,epsilon);

	(1)

a) Plantear el balance energético del manguito, en un instante genérico, en función de su temperatura.

Suponemos que en todo instante es isotermo aunque la conductividad térmica del acero inoxidable no es muy grande, k=17 W/(m·K) y se enfriaría más por los bordes que por el centro.

Cada cara del cilindro, de área A=Pi*D*L, radiará distinta energía porque la interior está parcialmente tapada por ella misma. Cada cara puede considerarse que forma parte de un recinto con solo dos nodos: la cara y el recinto de fondo, por lo que se puede aplicar la expresión general para cuerpos grises:

>	Q12:=rhs(eq13_6);

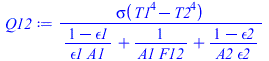(2)

que en el caso de recinto grande (A2>>A1) queda:

>	Q12:=subs(epsilon2=1,%);Q12:=epsilon1*A1*sigma*(T1^4-T2^4)/(1-epsilon1+epsilon1/F12);

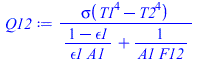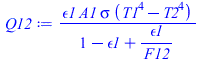	(3)

que en el caso de superficies convexas (F12=1) queda el tradicional Q=epsilon1*A1*sigma*(T1^4-T2^4), y para cuerpo negro (epsilon1=1) queda Q=A1*F12*sigma*(T1^4-T2^4), lo mismo que cuando F12 tiende a 0.

El factor geométrico desde la cara interior hacia el fondo del recinto será F12=1-F11, luego:

>	eqEB:=m*c*dT/dt=-Qconv-Qradext-Qradint;Qconv:=h*2*A*(T-T0);A:=Pi*D*L;A_:=evalf(subs(dat,%));Qradext:=epsilon*A*sigma*(T^4-T0^4);Qradint:=epsilon*A*(1-F11)*sigma*(T^4-T0^4)/(1-epsilon+epsilon/(1-F11));

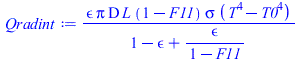	(4)

b) Determinar el valor de los siguientes factores geométricos: el mencionado en este caso y en los casos límite de longitud muy pequeña o muy grande (para diámetro fijo); el factor geométrico entre la superficie interior y una de las bases (aberturas); el factor geométrico entre las bases (aberturas).

>	eqF11_:=subs(dat,eqF11);eqF11_L_0:=F11=series(rhs(eqF11),L=0,2);F11_L_0=L/D;F11_L0=0;eqF11_Linf:=F11=asympt(rhs(eqF11),L,3);F11_Linf=1;F12:='(1-F11)/2';F12_:=subs(eqF11_,dat,%);F23:=1-F21;F21:='F12*A1/A2';F21_:=subs(A1=A,A2=Pi*D^2/4,eqF11_,dat,%);F23_:=1-F21_;

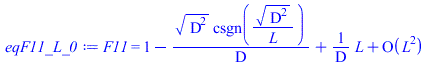	(5)

i.e. en nuestro caso es F11=0,59, i.e. el 59 % de lo que sale de la cara interior va directamente a ella misma, y el resto sale (41 %; 21 % por cada abertura). Con este último valor, F12=0,21, y la relación de áreas, calculamos F21=0,83 y por tanto, entre las bases F23=0,17 (i.e. desde una abertura a la otra).

Para cilindros muy cortos tiende a 0 como F11=D/L (con D<<L), y para muy largos tiende a 1 como 1-(D/L)/2, (con D<<L)..

c) Determinar los valores de los flujos de calor por convección y radiación en el instante inicial, suponiendo cuerpo negro.

>	Qconv0:=subs(T=T1,Qconv);Qconv0_:=subs(dat,evalf(subs(eqF11_,dat,Qconv0)));Qradext0:=subs(T=T1,Qradext);Qradext0_:=subs(dat,evalf(subs(epsilon=1,dat,Qradext0)));Qradint0:=subs(T=T1,Qradint);Qradint0_:=subs(dat,evalf(subs(eqF11_,epsilon=1,dat,Qradint0)));Qconvrad0:=Qconv0_+Qradext0_+Qradint0_;

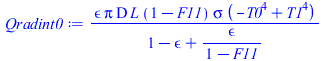	(6)

i.e.  inicialmente, por convección salen 440 W (220 W por cada cara), y por radiación salen 2070 W (1770 W por la cara externa y 300 W por la interna); en total 2510 W.

d) Determinar la velocidad inicial de enfriamiento en el caso anterior.

>	eqEB0:=m*c*dT/dt=-'Qconvrad0';eqm:=m=rho*Pi*D*L*delta;eqm_:=evalf(subs(Sdat,dat,%));eqEB0:=dT/dt=subs(dat,evalf(subs(eqm_,epsilon=1,Sdat,-Qconvrad0/(m*c))));

	(7)

i.e. al principio, los 0,245 g de chapa se enfrían unos 20 ºC cada segundo, por lo que el tiempo característico de enfriamiento (lo que tarda en disminuir a la mitad la diferencia de temperatura) será del orden de un minuto (1000-298)/20=35 s).

e) Volver a resolver el problema para el caso de acabado metálico no pintado.

>

Qconv0:=subs(T=T1,Qconv);Qconv0_:=subs(dat,evalf(subs(eqF11_,dat,Qconv0)));Qradext0:=subs(T=T1,Qradext);Qradext0_:=subs(dat,evalf(subs(Sdat,dat,Qradext0)));Qradint0:=sigma*(T1^4-T0^4)/((1-epsilon)/(A*epsilon)+1/(A*(1-F11)));Qradint0_:=subs(dat,evalf(subs(eqF11_,Sdat,dat,Qradint0)));Qconvrad0:=Qconv0_+Qradext0_+Qradint0_;eqEB0:=m*c*dT/dt=-'Qconvrad0';eqm:=m=rho*Pi*D*L*delta;eqm_:=subs(Sdat,dat,%);eqEB0:=dT/dt=evalf(subs(eqm_,Sdat,dat,-Qconvrad0/(m*c)));

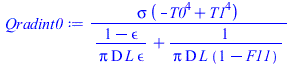	(8)

i.e. sin pintar, inicialmente, salen por convección los mismos 220 W por cada cara, pero por radiación salen 353 W por la cara externa y 275 W por la interna. En total salen 1070 W, por lo que se enfría más lentamente (tardará varios minutos).

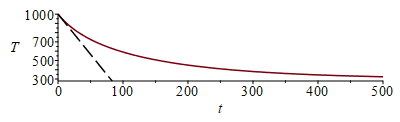
La evolución temporal sería:

>

eqBE:=m*c*diff(T(t),t)=-subs(T1=T(t),subs(T=T1,Qconv)+Qradext0+Qradint0);eqBE_:=evalf(subs(eqm_,eqF11,Sdat,dat,SI0,eqBE));T1_:=subs(dat,SI0,T1);solT:=dsolve([eqBE_,T(0)=T1_],numeric);with(plots):plT:=odeplot(solT,t=0..500):plT0:=plot(T1_+subs(SI0,rhs(eqEB0))*t,t=0..500, color=black,linestyle=dash):display({plT,plT0},view=[0..500,300..1000]);

>