>	restart:#"m13_p31"

Se trata de estudiar la transmisión de calor en régimen estacionario entre las caras interiores de un perfil cuya sección recta es un triángulo equilátero de 0,1 m de lado. Se supone que las tres caras están aisladas en las uniones, y que se mantienen dos de ellas a 300 K y la otra a 100 K. Esta última tiene una emisividad 1=0,9, y las otras dos tienen 2=0,5 y 3=0,1. Se pide:
a) Plantear las ecuaciones nodales que resuelven el problema.
b) Calcular las exitancias en cada cara.
c) Calor intercambiado en cada cara.
Datos:

>	with(RealDomain):read`../therm_proc.m`:with(therm_proc):

>	dat:=[L=0.1*m_,T1=100*K_,T2=300*K_,T3=300*K_,epsilon1=0.9,epsilon2=0.5,epsilon3=0.1];dat:=op(dat),Const,SI1,SI2:

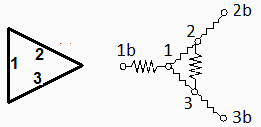
a) Plantear las ecuaciones nodales que resuelven el problema.

Sea Mib la emitancia de cuerpo negro (Mib=sigma*T^4), y Mi la exitancia (M=epsilon*Mb+(1-epsilon)*E).

Las ecuaciones generales para un recinto compuesto por 3 nodos no cóncavos (i.e. con Fii=0) son (véase el circuito eléctrico equivalente):

>	eq1:=epsilon1*A1*(M1b-M1)/(1-epsilon1)=A1*F12*(M1-M2)+A1*F13*(M1-M3);eq2:=epsilon2*A2*(M2b-M2)/(1-epsilon2)=A2*F21*(M2-M1)+A2*F23*(M2-M3);eq3:=epsilon3*A3*(M3b-M3)/(1-epsilon3)=A3*F31*(M3-M1)+A3*F32*(M3-M2);

	(1)

b) Calcular las exitancias en cada cara.

La solución general está aquí, pero no se imprime por su gran extensión (más de una página):

>	sol:=solve({eq1,eq2,eq3},{M1,M2,M3}):

Para un triángulo equilátero, por simetría, los factores geométricos son F12=1/2,F13=1/2,F21=1/2,F23=1/2,F31=1/2,F32=1/2, y la solución general se reduce a:

>	sol_:=simplify(subs(F12=1/2,F13=1/2,F21=1/2,F23=1/2,F31=1/2,F32=1/2,sol));

(2)

que con los datos del enunciado da:

>	Mb=sigma*T^4;sol__:=simplify(subs(M1b=sigma*T1^4,M2b=sigma*T2^4,M3b=sigma*T3^4,dat,SI1,sol_));Mb_:=subs(dat,SI1,[M1b=sigma*T1^4,M2b=sigma*T2^4,M3b=sigma*T3^4]);M=epsilon*Mb+rho[IR]*E;M=epsilon*Mb+(1-epsilon)*E;

	(3)

que se interpreta como sigue:

-La cara 1, que está a T1=100 K y emitiría M1b=5,67 W/m2 si fuese negra, solo emite e1*M1b=0,9*5,67=5,1 W/m2, pero también refleja 23,5 W/m2 (su exitancia es M1=5,1+23,5=28,6 W/m2); la irradiancia que incide sobre ella es E1=23,5/0,1=235 W/m2.

-La cara 2, que está a T2=300 K y emitiría M2b=459 W/m2 si fuese negra, solo emite e2*M2b=0,5*459=230 W/m2, pero también refleja 53,4 W/m2 (su exitancia es M2=230+53,4=283,4 W/m2); la irradiancia que incide sobre ella es E2=53,4/0,5=107 W/m2.

-La cara 3, que está a T3=300 K y emitiría M3b=459 W/m2 si fuese negra, solo emite e3*M3b=0,1*459=46 W/m2, pero también refleja 140 W/m2 (su exitancia es M2=46+140=186 W/m2); la irradiancia que incide sobre ella es E3=140/0,9=156 W/m2.

c) Calor intercambiado en cada cara..

En cada cara, el calor entrante es:

>	Q1:=-lhs(eq1);Q1_1m:=subs(A1=L*1*m_,Mb_,sol__,dat,SI1,%);Q2:=-lhs(eq2);Q2_1m:=subs(A2=L*1*m_,Mb_,sol__,dat,SI1,%);Q3:=-lhs(eq3);Q3_1m:=subs(A3=L*1*m_,Mb_,sol__,dat,SI1,%);

	(4)

i.e. la cara 1 (que está a T1=100 K) recibe 20,6 W por metro de longitud, la cara 2 (a 300 K) cede 17,6 W/m, y la cara 3 (también a 300 K) cede 3 W/m. Para mantener las temperaturas indicadas, de la 1 habra que extraer por refrigeración exterior los 20,6 W/m, y en la 2 y la 3 se pueden poner resistencias eléctricas que disipen hacia dentr los 17,6 W/m y 3 W/m calculados.

NOTA. En radiación térmica, es corriente referirse al "calor intercambiado por radiación entre dos cuerpos"; e.g. en nuestro caso podríamos preguntarnos por el calor intercambiado entre la superficie 1 y la 2. En realidad, a lo que se refiere eso es al flujo radiativo neto, i.e. Q12=Phi21-Phi12, identificando el 'calor que recibe la superficie 1 procedente de la superficie 2' como la diferencia entre el flujo radiante que sale de 2 y llega a 1, menos el que sale de 1 y va a 2. Pero en realidad no se puede hablar de calor intercambiado entre dos cuerpos más que cuando uno envuelve completamente al otro (problema de dos nodos) pues el calor se define en Termodinámica como la energía que atraviesa la frontera de un sistema debido a la diferencia de temperatura con el exterior, i.e. solo se define en la frontera de un cuerpo, no entre dos cuerpos.

Si calculamos los flujos radiativos netos como se ha indicado, tenemos:

>

Q12:=op(1,rhs(eq1));Q12_1m:=subs(sol__,A1=L*1*m_,F12=1/2,dat,SI1,Q12);Q13:=op(2,rhs(eq1));Q13_1m:=subs(sol__,A1=L*1*m_,F13=1/2,dat,SI1,Q13);Q1_1m:=Q12_1m+Q13_1m;Q21:=op(1,rhs(eq2));Q21_1m:=subs(sol__,A2=L*1*m_,F21=1/2,dat,SI1,Q21);Q23:=op(2,rhs(eq2));Q23_1m:=subs(sol__,A2=L*1*m_,F23=1/2,dat,SI1,Q23);Q2_1m:=Q21_1m+Q23_1m;Q31:=op(1,rhs(eq3));Q31_1m:=subs(sol__,A3=L*1*m_,F31=1/2,dat,SI1,Q31);Q32:=op(2,rhs(eq3));Q32_1m:=subs(sol__,A3=L*1*m_,F32=1/2,dat,SI1,Q32);Q3_1m:=Q31_1m+Q32_1m;

	(5)

i.e. vemos que en cada cara los flujos netos sí son flujos de calor (la 1 recibe 20,6 W/m, la 2 cede 17,6 W/m, y la 3 cede 3 W/m). Pero se llegaría al absurdo de que la superficie 2 recibiría 4,85 W/m de la 3 estando ambas a la misma temperatura.

>