| > | restart:#"m11_p97 |
Para un estudio térmico de una pared de un módulo en un vehículo espacial se va a considerar una placa plana de CFRP de 5 mm de espesor con nervaduras en su cara exterior, del mismo material, formando una malla rectangular de 0,2 m de separación en una dirección, y 0,5 m en la otra. Todos estos refuerzos son de 4 mm de espesor y sobresalen 20 mm. La cara interior del panel está enfrentada a una pared interior que se mantiene permanentemente a 23 ºC, con espaciadores cuya influencia térmica se desprecia que mantienen un espacio vacío de 30 mm entre superficies. Para las propiedades del CFRP se tomarán =1500 kg/m3, c=1100 J/(kg·K), k=30 W/(m·K) en el plano del laminado, k=1 W/(m·K) en el transversal, y ==0,9 por ambas caras. Para la pared interior se tomará =0,7. Se pide:
a) Indicar cómo sería el mapa de temperaturas de la pared en régimen estacionario estando expuesta solo a la radiación de fondo.
b) Despreciando el efecto de las aletas, calcular las temperaturas que se alcanzarían en la pared en régimen estacionario, y el coeficiente lineal de transmitancia equivalente al intercambio radiativo, por cada lado.
c) Tomando el resultado anterior como temperatura en la raíz de los refuerzos, y con el coeficiente lineal de transmitancia calculado, resolver el problema unidimensional para determinar el flujo de calor en la raíz.
d) Ahora se va a estudiar el efecto térmico de los refuerzos considerando la pared plana (sin refuerzos) pero con unos sumideros de calor lineales de 5 W/m sustituyendo a los refuerzos. Calcular el perfil de temperatura T(x) en la pared entre los refuerzos separados 0,2 m considerando que los refuerzos perpendiculares (cada 0,5 m) no influyen.
e) Calcular el perfil de temperatura T(x,y) en la pared con el modelo anterior (i.e. pared plana con sumideros lineales sustituyendo a los refuerzos).
f) Volviendo al problema plano del apartado b), determinar la temperatura de la pared con sol frontal.
Datos:
| > | with(RealDomain):read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):interface(displayprecision=1); |
| > | dat:=[Lzp=5e-3*m_,Lxp=0.1*m_,Lyp=0.2*m_,Lxf=2e-3*m_,Lzf=0.02,T0=(23+273.15)*K_,Tinf=2.7*K_,rho=1500*kg_/m_^3,c=1100*J_/(kg_*K_),kpar=30*W_/(m_*K_),kper=1*W_/(m_*K_),epsilon1=0.9,alpha1=0.9,epsilon0=0.7,E=1361*W_/m_^2,qr=5*W_/m_];dat:=op(dat),Const,SI2,SI1: |
Se trata de hallar el campo de temperaturas a través de la pared reforzada que está entre la placa mantenida a 23 ºC y el espacio profundo a 2,7 K. En todo el problema, la simetría permite resolver solo el trozo comprendido entre la mitad de un larguero y el plano medio entre largueros. Para el modelo 1D:
| > | #plot(subs(dat,SI0,([[[0,Lzf+Lzp],[Lxf,Lzf+Lzp],[Lxf,Lzp],[Lxp,Lzp]],[[0,0],[Lxp,0]]])),scaling=constrained); |
a) Indicar cómo sería el mapa de temperaturas de la pared en régimen estacionario estando expuesta solo a la radiación de fondo.
Donde haya refuerzos se enfriará más porque tienen mayor conductancia. Por ejemplo, el perfil T(x) cortando entre largueros transversales (i.e. cortando por y=0.2 m) sería así (aunque el redondeo en los refuerzos casi no se apreciaría):

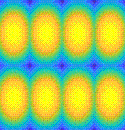
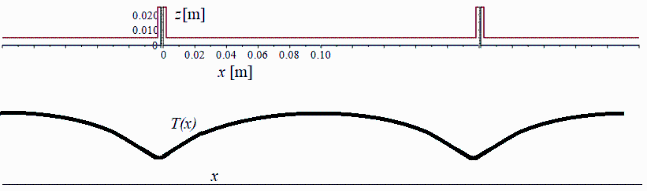
Fig. 1. a) Vista en planta y perfil de las paredes con la retícula de refuerzos. b) Mapa T(x,y) estacionario (con T(z)≠f(z)). c) Perfil T(x). d) Ejes.
b) Despreciando el efecto de las aletas, calcular las temperaturas que se alcanzarían en la pared en régimen estacionario, y el coeficiente lineal de transmitancia equivalente al intercambio radiativo, por cada lado.
Suponiendo geometría plana 1D entre la placa interior a 23 ºC y la pared de CFRP, i.e. solo dos nodos, el intercambio radiativo depende explícitamente de las emisividades (Ec. 37).
| > | eqEB1:=Q01=Q12;eqEB2:=Q12=Q2inf;Q2inf:=epsilon1*A*sigma*(T2^4-Tinf^4);Q12:=kper*A*(T1-T2)/Lzp;Q01:=sigma*(T0^4-T1^4)/((1-epsilon0)/(A0*epsilon0)+1/(F01*A0)+(1-epsilon1)/(A1*epsilon1));Q01:=A*sigma*(T0^4-T1^4)/(1/epsilon0+1/epsilon1-1);eqEB1_A:=subs(dat,SI0,eqEB1/A);eqEB2_A:=subs(dat,SI0,eqEB2/A);sol_:=fsolve({eqEB1_A,eqEB2_A},{T1,T2},{T1=100..400,T2=100..400});T1_:=subs(sol_,T1)*K_;'T1_'=TKC(%);T2_:=subs(sol_,T2)*K_;'T2_'=TKC(%);eqQ01:=Q=Q01;eqQ01_:=Q01_A=subs(sol_,dat,SI0,Q01/A)*W_/m_^2;eqQ12:=Q=Q12;eqQ12_:=Q12_A=subs(sol_,dat,SI0,Q12/A)*W_/m_^2;eqQ2inf:=Q=Q2inf;eqQ2inf_:=Q2inf_A=subs(sol_,dat,SI0,Q2inf/A)*W_/m_^2; |
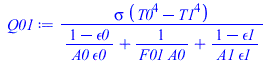 |
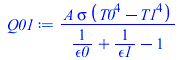 |
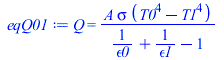 |
i.e. la cara interior de la placa quedaría a 238,8 K (-34,4 ºC) y la exterioe a 238,0 K (-35,2) ºC. Vemos que la diferencia es pequeña, DT=0,8 K, así que se podía haber resuelto considerando un nodo único (placa isoterma), como se hace a continuación. El flujo de calor que atraviesa la pared es de 164 W/m2.
| > | eqEBp:=subs(T1=T,Q01)=subs(T2=T,Q2inf);eqEBp_:=T4=solve(subs(T^4=T4_,eqEBp),T4_);Tm:=sqrt(sqrt(T4));Tm_:=max(evalf(subs(eqEBp_,dat,SI0,T4^(1/4))))*K_;'Tm_'=TKC(%);eqEBp_:=subs(T=Tm_,dat,eqEBp);eqh1_:=h1=subs(dat,rhs(eqEBp_)/(A*(T0-Tm_)));eqh2_:=h2=subs(dat,rhs(eqEBp_)/(A*(Tm_-Tinf)));Tm:='Tm':eqQnet:=h1*A*(T-T0)+h2*A*(T-Tinf)=ht*A*(T-Teff);eqht:=ht=h1+h2;eqTeff:=Teff=(h1*T0+h2*Tinf)/(h1+h2);eqht_:=subs(eqh1_,eqh2_,eqht);eqTeff_:=subs(eqh1_,eqh2_,dat,eqTeff);'Teff'=TKC(rhs(%)); |
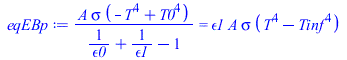 |
i.e. la pared, a Tm=238,3 K (-34,9 ºC), por dentro recibe calor del entorno a 23 ºC con un coeficiente lineal de h1=2,84 W/(m2·K), y hacia fuera evacúa a a 2,7 K con un coeficiente lineal de h2=0,70 W/(m2·K), lo que equivale a un coeficiente total ht=3,54 W/(m2·K) respecto a una Tinf_efectiva Teff=238,3 K (-34,9 ºC) que coincide con la de equilibrio de la pared, ya que Qnet=ht*A*(T-Teff)=0 cuando T=Tm.
c) Tomando el resultado anterior como temperatura en la raíz de los refuerzos, y con el coeficiente lineal de transmitancia calculado, resolver el problema unidimensional para determinar el flujo de calor en la raíz.
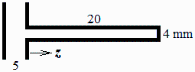
Se trata de un problema típico de aletas que admite solución analítica (Heat conduction; Table 4). Tomaremos la k en dirección z como kpar porque la construcción de los refuerzos con CFRP será con laminado continuo.
| > | eqTfin:=(T(z)-Tinf)/(Tm-Tinf)=cosh(m*(L-z))/cosh(m*L);eqQfin:=Q0=tanh(m*L)*(Tm-Tinf)*sqrt(p*h2*kpar*A);eqm:=m=sqrt(h2*p/(k*A));p=2;A=2*Lxf;k=kpar;eqm_:=m=evalf(subs(eqh2_,dat,SI0,sqrt(2*h2/(kpar*2*Lxf))))/m_;eqQfin_:=lhs(eqQfin)=evalf(subs(Tm=Tm_,eqm_,eqh2_,L=Lzf,p=2,A=2*Lxf,dat,SI0,rhs(eqQfin)))*W_/m_;eqT:=T(z)=Tinf+(Tm-Tinf)*cosh(m*(L-z))/cosh(m*L);eqT_:=evalf(subs(Tm=Tm_,eqm_,eqh2_,L=Lzf,dat,SI0,%));plot(rhs(%),z=0..subs(dat,SI0,Lzf),T_K=237..239);Ttip:=evalf(subs(z=subs(dat,SI0,Lzf),rhs(eqT_)))*K_;'Ttip'=TKC(%); |
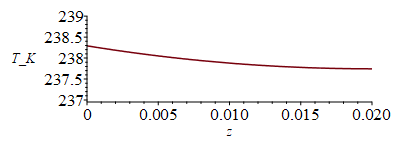 |
i.e. los refuerzos añaden una evacuación de calor en su raíz de Q0=6,6 W/m, alcanzando una temperatura de 237,7 K (-35,4 ºC) en la punta (0,5 ºC menor que la de la raíz). Un chequeo rápido es considerar el calor que evacuaría la superficie adicional si estuviese a la temperatura de la raíz, Qaleta=h2·Aaleta·(Traíz-Tinf)=0,70·(2·0,02)·(238,3-2,7)=6,6 W/m.
d) Ahora se va a estudiar el efecto térmico de los refuerzos considerando la pared plana (sin refuerzos) pero con unos sumideros de calor lineales de 5 W/m sustituyendo a los refuerzos. Calcular el perfil de temperatura T(x) en la pared entre los refuerzos separados 0,2 m considerando que los refuerzos perpendiculares (cada 0,5 m) no influyen.
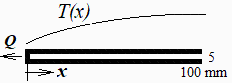
Se trata de otro problema de aletas (ahora en el plano de la pared) con un sumidero de calor en la raíz (Q0=-5 W/m en x=0) y extremo adiabático (Q=0 en x=Lxp=0,1 m), con pérdidas laterales lineales con la temperatura local. Sería más apropiado tomar los 6,5 W/m antes calculados, pero nos atendremos al valor del enunciado, que tal vez tenga en cuenta la re-radiación térmica entre pared y refuerzos. La solución analítica (Heat conduction; Table 4) es:
| > | eqT:=(T(x)-Teff)*sqrt(p*h*k*A)/Q0=cosh(m*(L-x))/sinh(m*L);Troot:=Teff+Q0/(sqrt(p*h*k*A)*tanh(m*L));Ttip:=Teff+Q0/(sqrt(p*h*k*A)*sinh(m*L)); |
donde la Teff es la temperatura media ponderada del entorno, Teff=Tm=238,3 K=-34,9 ºC, antes calculada para una h_total=h1+h2. La Q0 será la mitad de un sumidero, Q0=qr/2, por simetría.
| > | eqm:=m=sqrt(h*p/(k*A));h=h1+h2;p=1;k=kpar;A=Lzp;eqm:=m=sqrt((h1+h2)/(kpar*Lzp));eqm_:=m=evalf(subs(eqh1_,eqh2_,Tm=Tm_,dat,SI0,rhs(eqm)))/m_;eqT:=T(x)=Tm+Q0*cosh(m*(Lxp-x))/sinh(m*Lxp)/sqrt((h1+h2)*kpar*Lzp);Q0=subs(dat,SI0,-qr/2)*W/m;;eqT_:=evalf(subs(eqm_,Tm=Tm_,eqh1_,eqh2_,Q0=-qr/2,dat,SI0,eqT));plot(rhs(%),x=0..subs(dat,SI0,Lxp),T_C=230..232);Troot_:=evalf(subs(Teff=Tm_,eqm_,L=Lxp,Q0=-qr/2,p=1,h=h1+h2,eqh1_,eqh2_,k=kpar,A=Lzp,dat,SI0,Troot))*K_;'Troot_'=TKC(%);Ttip_:=evalf(subs(Teff=Tm_,eqm_,L=Lxp,Q0=-qr/2,p=1,h=h1+h2,eqh1_,eqh2_,k=kpar,A=Lzp,dat,SI0,Ttip))*K_;'Ttip_'=TKC(%); |
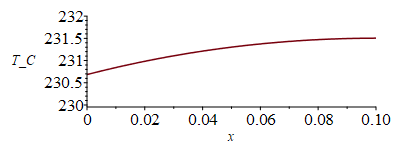 |
i.e. las aletas añaden área de paso al flujo de calor, bajando no solo la temperatura en su encastre, sino en toda la pared, que pasa de tener una temperatura uniforme de 238,3 K (-34,9 ºC), a tener en el encastre Troot=230,7 K (-42,5 ºC), y 231,5 K (-41,7 ºC, 0,8 K más) en el punto medio entre largueros (separados 20 cm).
e) Calcular el perfil de temperatura T(x,y) en la pared con el modelo anterior (i.e. pared plana con sumideros lineales sustituyendo a los refuerzos).
Resuelto el problema 2D con Matlab, partiendo de toda la placa a Tini=238,3 K hasta alcanzar el estado estacionario, el resultado es:
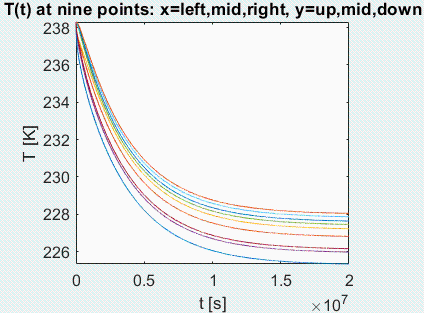
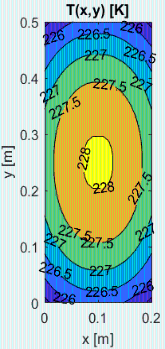
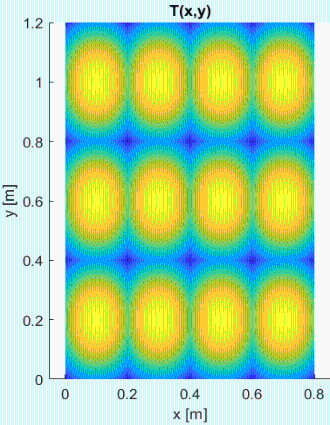
Fig. 2. a) Enfriamiento T(x,y,t) debido a los sumideros (Tini=238 K sin sumideros). b) T(x,y) estacionario. c) Mapa T(x,y) extendido.
i.e. en el estacionario (discretizando con 10 tramos en 'x' y 20 en 'y') la Tmin se da en el cruce de aletas y vale Tmin=225,3 K, y la Tmax se da en el centro de los tramos y vale Tmax=228,0 K (la diferencia es 2,7 K). Para estimar la bondad de la simulación 2D se ha aumentado la separación entre aletas en el eje 'y', para que el modelo sea casi 1D, obteniéndose con la misma discretización Tmin=229,5 K (en vez del valor teórico antes calculado, Troot=230,7 K) y Tmax=230,2 K en vez de Ttip=231,5 K).
f) Volviendo al problema plano del apartado b), determinar la temperatura de la pared con sol frontal.
| > | eqEB1:='Q01'='Q12';eqEB2:='Q12'+alpha1*E*A='Q2inf';eqEB1_A:=subs(dat,SI0,eqEB1/A);eqEB2_A:=subs(dat,SI0,expand(eqEB2/A));sol_:=fsolve({eqEB1_A,eqEB2_A},{T1,T2},{T1=100..400,T2=100..400});T1_:=subs(sol_,T1)*K_;'T1_'=TKC(%);T2_:=subs(sol_,T2)*K_;'T2_'=TKC(%);eqQ01:=Q=Q01;eqQ01_:=Q01_A=subs(sol_,dat,SI0,Q01/A)*W_/m_^2;eqQ12:=Q=Q12;eqQ12_:=Q12_A=subs(sol_,dat,SI0,Q12/A)*W_/m_^2;eqQ2inf:=Q=Q2inf;eqQ2inf_:=Q2inf_A=subs(sol_,dat,SI0,Q2inf/A)*W_/m_^2; |
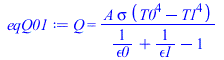 |
i.e. con sol, la placa queda a 361 K (88 ºC) por el interior y a casi 363 K (90 ºC), en vez de a los 239 y 238 K sin sol, radiando 883 W/m2 hacia afuera y 342 W/m2 hacia adentro (compensando los 0,9·1361=1225 W/m2 de absorción solar), con lo que la pared fija a 23 ºC en el interir, que antes perdía calor, ahora lo gana.
| > |