>	restart:#"m11_p95"

Calcular el campo de temperaturas en un sólido cúbico de 0,1 m de lado y conductividad térmica k=10 W/(m·K), con una disipación de energía interna uniforme de  =10 W, estando aislado térmicamente por todas sus caras menos una, y con Tm=100 ºC en la cara opuesta.).

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	dat:=[L=0.1*m_,k=10*W_/(m_*K_),Wdis=10*W_,Tm=(100+273.15)*K_];dat:=op(dat),Const,SI2,SI1:

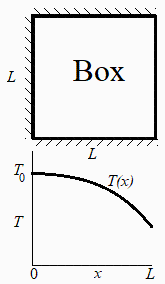
Se trata de un sencillo problema de trasmisión de calor unidimensional plano. Tomando el eje x en la dirección del flujo (la T no varía en las otras direcciones por estar aislado lateralmente). La ecuación del calor y su solución estacionaria son:

>	eqH:=rho*c*Diff(T(x,t),t)=k*Diff(T(x,t),x,x)+phi;eqphi:=phi=Wdis/L^3;eqH_:=0=k*diff(T(x),x,x)+phi;eqBC1:=T(x)[x=0]=Tm;eqBC2:=diff(T(x),x)[x=0]=0;sol:=dsolve({eqH_,T(0)=Tm,D(T)(0)=0},T(x));sol_:=subs(eqphi,sol);TL=T(x)[x=L];TL_:=subs(x=L,rhs(sol_));

	(1)

que con los valores dados es:

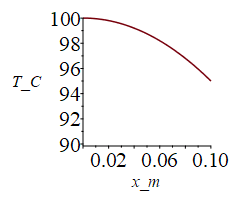
>	TL__:=subs(dat,TL_);'TL__'=TKC(%);sol__:=subs(dat,SI0,sol_);plot(subs(x=x_m,rhs(%)-273.15),x_m=0..0.1,T_C=90..100);