p911.html

> restart:#"m11_p91"

Se quiere estimar la temperatura de una madera de 3 cm de espesor que flota en una piscina bajo el sol de mediodía. La temperatura ambiente es 30 ºC y la del agua 25 ºC. Suponiendo unos coeficientes convectivos con el aire y el agua de 20 W/(m2•K) y 200 W/(m2•K), respectivamente, y que la irradiancia solar es 1000 W/m2, se pide:
a) Temperatura de la madera suponiendo que es uniforme.
b) Influencia de la conductividad térmica.
c) Solución transitoria si, a partir del estado anterior, deja de estar expuesta al sol.

Datos:

> read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

> su:="Madera_de_pino":dat:=[delta=0.03*m_,Ta=(30+273)*K_,Tw=(25+273)*K_,ha=20*W_/(m_^2*K_),hw=200*W_/(m_^2*K_),E=1000*W_/m_^2];

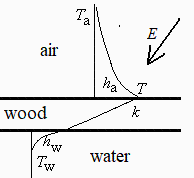
Tomaremos las siguientes propiedades para la madera:

> dat:=op(dat),get_sol_data(su),Const,SI2,SI1:Madera_de_pino_rho_c_k_alpha_epsilon:=subs(dat,[rho,c,k,alpha,epsilon]);

a) Temperatura de la madera suponiendo que es uniforme.

Usaremos un modelo unidimensional (1D), i.e. sin tener en cuenta efectos laterales.

Supondremos despreciable la radiación emitida por la madera (para que el problema sea lineal), o que el coeficiente convectivo ya incluye el efecto de la radiación. Sin embargo, con cielo despejado, las pérdidas de calor por radiación con la temperatura equivalente del cielo (que podría ser de unos 30 ºC bajo cero), pueden ser relevantes.

El balance energético estacionario con T=cte sería:

> eqBE:=Qin=Qout;eqBE:=alpha*E*A=ha*A*(T-Ta)+hw*A*(T-Tw);T_:=solve(%,T);T__:=subs(dat,%);'T1__'=TKC(%);

(1)

i.e. si toda la madera estuviese a la misma temperatura, ésta sería de 28 ºC.

Si añadimos el intercambio radiativo en el infrarrojo, suponiendo que la temperatura de radiación (temperatura del cielo) es la misma que la del aire, sería

> eqBE:=Qin=Qout;eqBE:=alpha*E*A=epsilon*A*sigma*(T^4-Ta^4)+ha*A*(T-Ta)+hw*A*(T-Tw);eqBE_:=subs(dat,SI0,expand(%/A));T_:=fsolve(%,T=200..500)*K_;'T1_'=TKC(%);

(2)

i.e. vemos que la radiación IR apenas influye (incluso con Tsky=Ta-50=253 K solo pasaría de 28 ºC a 27 ºC).

b) Influencia de la conductividad térmica.

El balance energético estacionario con T(x) sería:

> eqBEsup:=alpha*E*A=ha*A*(Tsup-Ta)+k*A*(Tsup-Tinf)/delta;eqBEinf:=k*A*(Tsup-Tinf)/delta=hw*A*(Tinf-Tw);sol:=solve(expand({eqBEsup/A,eqBEinf/A}),{Tsup,Tinf});sol_:=subs(dat,%);Tsup_:=subs(sol_,Tsup);'Tsup'=TKC(%);Tinf_:=subs(sol_,Tinf);'Tinf'=TKC(%);

$Typesetting:-mprintslash([sol_ := {Tinf = `+`(`*`(298.6862745, `*`(K_))), Tsup = `+`(`*`(326.1372549, `*`(K_)))}], [{Tinf = `+`(`*`(298.6862745, `*`(K_))), Tsup = `+`(`*`(326.1372549, `*`(K_)))}])$

(3)

i.e. vemos la enorme influencia de la conductividad: la parte superior quedaría a 53 ºC y la inferior a 25,5 ºC, casi a la del agua..

Si añadimos el término radiativo :

> eqBEsup:=alpha*E*A=epsilon*A*sigma*(Tsup^4-Ta^4)+ha*A*(Tsup-Ta)+k*A*(Tsup-Tinf)/delta;eqBEinf:=k*A*(Tsup-Tinf)/delta=hw*A*(Tinf-Tw);eqs_:=subs(dat,SI0,expand({eqBEsup/A,eqBEinf/A}));sol_:=fsolve(eqs_,{Tsup,Tinf},{Tsup=200..500,Tinf=200..500});Tsup_:=subs(sol_,Tsup)*K_;'Tsup_'=TKC(%);Tinf_:=subs(sol_,Tinf)*K_;'Tinf_'=TKC(%);

$Typesetting:-mprintslash([eqs_ := {600.0 = `+`(`-`(6490.126383), `*`(0.51030e-7, `*`(`^`(Tsup, 4))), `*`(25.00000000, `*`(Tsup)), `-`(`*`(5.000000000, `*`(Tinf)))), `+`(`*`(5.000000000, `*`(Tsup)), `-...$

$Typesetting:-mprintslash([sol_ := {Tinf = 298.5734020, Tsup = 321.5094826}], [{Tinf = 298.5734020, Tsup = 321.5094826}])$

(4)

i.e. vemos que la Tsup baja de 53 ºC a 48 ºC y la inferior apenas varía.

c) Solución transitoria si, a partir del estado anterior, deja de estar expuesta al sol.

Para el transitorio hace falta el cálculo numérico.Sea N el número de tramos (N+1 puntos): 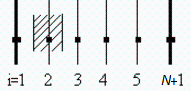con i=1 para la cara inferior, e i=N+1 para la superior.

> eq_Heat_1D:=rho*c*diff(T(x,t),t)=k*diff(T(x,t),x,x);i:='i':eqi:=T[j+1,i]=T[j,i]+Fo*(T[j,i+1]-2*T[j,i]+T[j,i-1]);eq0:=rho*c*Dx*(T[j+1,1]-T[j,1])/Dt=k*(T[j,2]-T[j,1])/Dx-hw*(T[j,1]-Tw);eq0:=T[j+1,1]=T[j,1]+Dt_rcDx*(k*(T[j,2]-T[j,1])/Dx-hw*(T[j,1]-Tw)); eqN:=rho*c*Dx*(T[j+1,N+1]-T[j,N+1])/Dt=alpha*E-epsilon*sigma*(T[j,N+1]^4-Ta^4)-ha*(T[j,N+1]-Ta)-k*(T[j,N+1]-T[j,N])/Dx;eqN:=T[j+1,N+1]=T[j,N+1]+Dt_rcDx*(alpha*E-epsilon*sigma*(T[N+1,j]^4-Ta^4)-ha*(T[j,N+1]-Ta)-(T[j,N+1]-T[j,N])*k/Dx);

(5)

> N:=20;M:=1000;tsim:=5000;Dx:=subs(dat,SI0,delta/N);Dt:=evalf(tsim/M);Tn:=Matrix(1..M,1..N+1,0);eqFo:=Fo=k*'Dt'/(rho*c*'Dx'^2);Fo_:=subs(dat,SI0,rhs(%));Dt_rcDx:=subs(dat,SI0,Dt/(rho*c*Dx));sigma_:=subs(dat,SI0,sigma):j:=1:for i from 1 to N+1 do Tn[j,i]:=subs(dat,SI0,Tinf_+((i-1)/N)*(Tsup_-Tinf_));od:print(`j=`,j,Tn[j,1..N+1]);Tw_:=subs(dat,SI0,Tw):Ta_:=subs(dat,SI0,Ta):hw_:=subs(dat,SI0,hw):ha_:=subs(dat,SI0,ha):k_:=subs(dat,SI0,k):E_:=subs(dat,SI0,0*E);

Typesetting:-mprintslash([Tn := RTABLE(18446745831552994950, anything, Matrix, rectangular, Fortran_order, [], 2, 1 .. 1000, 1 .. 21)], [Matrix(%id = 18446745831552994950)])

Typesetting:-mprintslash([`j=`, 1, RTABLE(18446745831552990014, anything, Vector[row], rectangular, Fortran_order, [], 1, 1 .. 21)], [`j=`, 1, Vector[row](%id = 18446745831552990014)])

(6)

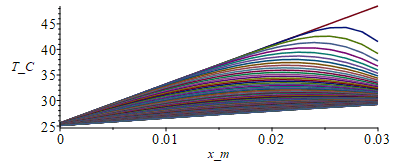
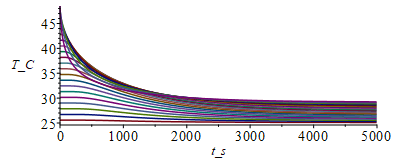
y la evolución es:

> T0_:=273:for j from 1 to M-1 do Tn[j+1,1]:=Tn[j,1]+Dt_rcDx*(k_*(Tn[j,2]-Tn[j,1])/Dx-hw_*(Tn[j,1]-Tw_));Tn[j+1,N+1]:=Tn[j,N+1]+Dt_rcDx*(subs(dat,alpha)*E_-subs(dat,epsilon)*sigma_*(Tn[j,N+1]^4-Ta_^4)-ha_*(Tn[j,N+1]-Ta_)-(Tn[j,N+1]-Tn[j,N])*k_/Dx);for i from 2 to N do Tn[j+1,i]:=Tn[j,i]+Fo_*(Tn[j,i-1]-2*Tn[j,i]+Tn[j,i+1]);od:od: Tmax:=max(Tn)-T0_:'Tmax_ini'=%*`ºC`;Dm:=10:sx:=seq([seq([i*Dx-Dx,Tn[j*Dm+1,i]-T0_],i=1..N+1)],j=0..(M-1)/Dm):plot([sx],x_m=0..0.03,T_C=25..Tmax);st:=seq([seq([j*Dt-Dt,Tn[j,i]-T0_],j=1..M)],i=1..N+1):plot([st],t_s=0..tsim,T_C=25..Tmax);Tmax_fin:=max(Tn(M,1..N+1))*K_:'Tmax_fin'=TKC(%);

Plot_2d

Plot_2d

(7)

i.e. empieza con la T(x) lineal de 25 ºC a 49 ºC, y acaba otra vez con la T(x) lineal de 25 ºC a 29 ºC, pero vemos que al principio se enfría más la cara superior que las inmediatas inferiores.