| > | restart:#"m11_90" |
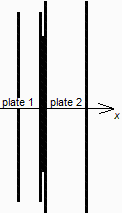
Para el control térmico de una caja electrónica en un vehículo espacial, se quiere estudiar el proceso de calentamiento producido por una lámina calefactora de kapton de 100×100 mm2 de área y 0,2 mm de espesor, con resistencias eléctricas embebidas de 20 W, colocada en contacto entre dos placas de mayor área, una de d1=4 mm de espesor y propiedades k1=0,1 W/(m2·K), 1=2000 kg/m3, c1=2000 J/(kg·K), y la otra de d2=10 mm de espesor y k2=1 W/(m2·K), 2=1000 kg/m3, c2=1000 J/(kg·K), respectivamente. Se pide:
a) Suponiendo que se llegase al estado estacionario desde un estado inicial a 0 ºC manteniendo las temperaturas externas fijas (a 0 ºC), determinar el calor que saldría por cada cara, la temperatura máxima alcanzada, y la duración del transitorio.
b) Solución analítica de la evolución transversal de las temperaturas, T(x,t), suponiendo que todo el calor va hacia un lado que puede suponerse semi-infinito.
c) Evolución de los flujos de calor y de los saltos de temperaturas con el tiempo, para cada placa, aplicado el modelo semi-infinito a cada una.
d) Simulación numérica de la evolución transversal de las temperaturas, T(x,t), al conectar el calentador desde un instante inicial en el que todo está a 0 ºC, suponiendo que las caras externas son adiabáticas, y comparación con el resultado del modelo semi-infinito.
e) Evolución T(x,t) si se apaga el calentador tras 100 s de funcionamiento.
f) Estimación de las pérdidas laterales en las placas, debido al menor tamaño del calentador.
Datos:
| > | read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):with(plots): |
| > | dat:=[A=0.01*m_^2,Q=20*W_,T0=(0+273.15)*K_];dat1:=L=0.004*m_,a=k/(rho*c),k=0.1*W_/(m_*K_),rho=2000*kg_/m_^3,c=2000*J_/(kg_*K_);dat2:=L=0.01*m_,a=k/(rho*c),k=1*W_/(m_*K_),rho=1000*kg_/m_^3,c=1000*J_/(kg_*K_);dat:=op(dat),Const,SI2,SI1:eq_q:=Q/A=subs(dat,Q/A);a1_:=evalf(subs(dat1,dat,a))*1e6*mm_^2/m_^2;a2_:=evalf(subs(dat2,dat,a))*1e6*mm_^2/m_^2; |
a) Suponiendo que se llegase al estado estacionario desde un estado inicial a 0 ºC manteniendo las temperaturas externas fijas (a 0 ºC), determinar el calor que saldría por cada cara, la temperatura máxima alcanzada, y la duración del transitorio.
Despreciando el espesor del calefactor (0,2 mm) frente a los espesores de las placas (4 mm y 10 mm), y aproximando por el modelo unidimensional (i.e. despreciando las pérdidas de calor en las direcciones z e y), la solución estacionaria tendrá perfiles T(x) lineales desde la Tmax en el calefactor hasta los 273 K (0º) fijados para las caras exteriores.
| > | eqq:=q=Q/A;eqq_:=subs(dat,%);eqq1:=q1=k1*(Tm-T0)/L1;eqq2:=q2=k2*(Tm-T0)/L2;eqq:=q=q1+q2;eqq__:=subs(eqq1,eqq2,eqq);eqTst:=Tm=solve(%,Tm);eqTst_:=subs(eqq_,k1=k,L1=L,dat1,k2=k,L2=L,dat2,dat,%);Tm=TKC(rhs(%));eqq1_:=subs(eqTst_,k1=k,L1=L,dat1,dat,eqq1);eqq2_:=subs(eqTst_,k2=k,L2=L,dat2,dat,eqq2);eqtc:=tc=rho*c*L^2/k;eqtc1:=tc1=subs(dat1,dat,rhs(eqtc));eqtc2:=tc2=subs(dat2,dat,rhs(eqtc)); |
| (1) |
i.e. con el modelo 1D, se generan 2000 W/m2 en la lámina calefactora, de los que 400 W/m2 fluyen hacia la placa 1 (la más delgada) y 1600 W/m2 hacia la placa 2. La temperatura que alcanzaría la resistencia es Tm=16 ºC, y el tiempos característico hasta alcanzar el régimen estacionario sería de unos 640 s (más de 10 minutos), aunque la placa 2 alcanzaría el régimen mucho antes (en unos 100 s).
Otra manera de estimar la duración es calcular el tiempo que tardaría un cuerpo aislado en alcanzar esa temperatura con esa disipación, tc=mcDT/Q=(rho1*c1*L1+rho2*c2*L2)*DT/q=(2000*1000*0,004+1000*1000*0,010)*16/2000=208 s, o mejor la mitad puesto que no todo se calienta los 16 ºC del máximo.
b) Solución analítica de la evolución transversal de las temperaturas, T(x,t), suponiendo que todo el calor va hacia un lado que puede suponerse semi-infinito.
La solución teórica 1D para una deposición frontal de potencia constante q (q=2000 W/m2) en un medio semiinfinito es (Problem 2 in Table 5 of Energy deposition in unbounded media, in Heat conduction):
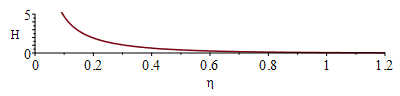
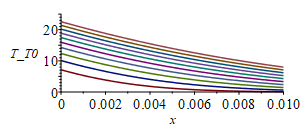
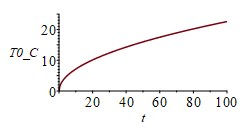
| > | eqT:=T(x,t)-T0=(q*x/k)*Eta;Eta:=exp(-eta^2)/(sqrt(Pi)*eta)+erf(eta)-1;eqeta:=eta=x/sqrt(4*a*t);eqT0:=T(0,t)-T0=2*q*sqrt(t/(Pi*rho*c*k));plot(Eta,eta=0..1.2,'Eta'=0..5);eqT_:=subs(eqeta,eqT):eqTp:=dT/dx=diff(rhs(eqT_),x):eqTp0:=(dT/dx)[x=0]=convert(series(rhs(eqTp),x=0,2),polynom);T_T0:=subs(eqeta,rhs(eqT));T_T0_:=subs(eqq_,dat2,dat,SI0,T_T0);pl2:=plot([seq(subs(t=10*i,T_T0_),i=1..10)],x=0..subs(dat2,SI0,L),'T_T0'=0..25);plot(subs(eqq_,dat2,SI0,rhs(eqT0)),t=0..100,T0_C=0..25); |
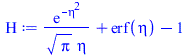 |
 |
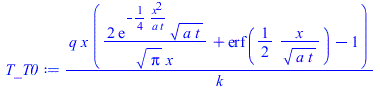 |
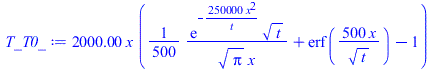 |
 |
 |
i.e. se trata de una solución de semejanza en la variable eta, con la función Eta(eta) representada en la figura de arriba (comprobamos que en x=0 se cumple q=-k*dT/dx).
En el gráfico T(x) se ha representado la evolución T(x,t)-T0 a lo largo del espesor para diversos tiempos (entre cada línea transcurren 10 s) para la placa 2 (la gruesa) hasta los tc=100 s antes calculados. No es comparable este último perfil con el perfil lineal del caso estacionario del apartado anterior (que iba de T-T0=16 ºC a 0, porque aquí no se fija la Text-T0=0 (aparte de que aquí se envían todos los 2000 W/m2 hacia este lado).
En el gráfico T(t), último, se ha representado la evolución T(0,t)-T0 en función del tiempo (i.e. la evolución de la temperatura del calefactor). Nótese que la misma resistencia eléctrica puede usarse para calefacción y como termómetro (a partir de la relación entre resistividad y temperatura), por lo que si se miden a la vez q y T(0,t), la ecuación eqT0 anterior permite determinar la conductividad térmica del material (en realidad solo la efusividad, e=sqrt(k·rho·c)).
c) Evolución de los flujos de calor y de los saltos de temperaturas con el tiempo, para cada placa, aplicado el modelo semi-infinito a cada una.
Se sabe que el reparto de flujos de calor en el contacto entre sólidos semi-infinitos es proporcional a las efusividades térmicas, e=sqrt(rho·c·k), como se desprende la la eqT0 anterior; i.e.: como la T(x=0) ha de ser la misma, q1/e1=q2/e2 y q1+q2=q, de dionde:
| > | q1:=q*sqrt(rho1*c1*k1)/(sqrt(rho1*c1*k1)+sqrt(rho2*c2*k2));q2:=q*sqrt(rho2*c2*k2)/(sqrt(rho1*c1*k1)+sqrt(rho2*c2*k2));q_:=rhs(eqq_);q1_:=subs(q=q_,rho1=rho,c1=c,k1=k,dat1,rho2=rho,c2=c,k2=k,dat2,q1);q2_:=subs(q=q_,rho1=rho,c1=c,k1=k,dat1,rho2=rho,c2=c,k2=k,dat2,q2); |
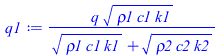 |
|
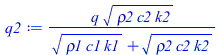 |
|
| (2) |
i.e. de los 2000 W/m2, 775 W/m2 van a 1 (entran en la placa delgada) y 1225 W/m2 van a 2 (entran en la placa gruesa), y este reparto no varía con el tiempo mientras sea válido el modelo doblemente semi-infinito. En valores absolutos, de los 20 W, 12,3 W van hacia la derecha y 7,7 W hacia la izquierda. Como comprobación, aplicamos la solución semiinfinita a cada lado:
| > | eqT0_1:=evalf(subs(q=q1_,dat1,SI0,rhs(eqT0)));eqT0_2:=evalf(subs(q=q2_,dat2,SI0,rhs(eqT0)));plot([eqT0_1,eqT0_2],t=0..1e2,Tmax_T0=0..15); |
 |
efectivamente, coinciden, y vemos que al cabo de unos 100 s ha subido unos 15 ºC la temperatura en el contacto. Si calculamos y dibujamos las temperatures exteriores en función del tiempo:
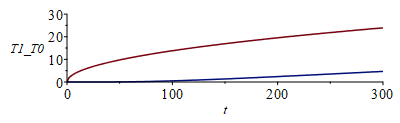
| > | plot([subs(x=1e-6,q=q1_,dat1,dat,SI0,rhs(eqT_)),subs(x=L,q=q1_,dat1,dat,SI0,rhs(eqT_))],t=0..300,T1_T0=0..30);plot([subs(x=1e-6,q=q2_,dat2,dat,SI0,rhs(eqT_)),subs(x=L,q=q2_,dat2,dat,SI0,rhs(eqT_))],t=0..300,T2_T0=0..30); |
 |
|
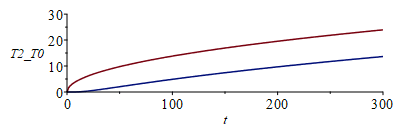 |
donde se aprecia que el salto en la placa 1 va creciendo, pero en la 2 se estabiliza. Podemos calcular estos saltos con el modelo estacionario y los flujos conocidos:
| > | eqDT:=q=k*DT/L;DT_:=q*L/k;DT1_:=subs(q=q1_,dat1,dat,DT_);DT2_:=subs(q=q2_,dat2,dat,DT_); |
| (3) |
i.e. entre las caras de la placa 1, DT tiende a unos 31 ºC (en la figura ya llega a unos 20 ºC al cabo de 300 s), mientras que entre las caras de la placa 2 (de mayor espesor, pero más difusiva), DT tiende a unos 12 ºC (como se aprecia en la figura)..
d) Simulación numérica de la evolución transversal de las temperaturas, T(x,t), al conectar el calentador desde un instante inicial en el que todo está a 0 ºC, suponiendo que las caras externas son adiabáticas, y comparación con el resultado del modelo semi-infinito.
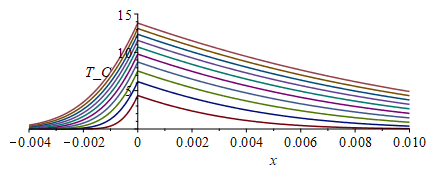
El caso de bordes adiabáticos se ha resuelto con Matlab, y se ha obtenido:

y con el modelo doblemente semi-infinito sería:
| > | T_T0:=subs(eqeta,rhs(eqT));T1_T0:=subs(q=q1_,dat1,dat,SI0,T_T0);pl1:=plot([seq(subs(x=-x,t=10*i,T1_T0),i=1..10)],x=-subs(dat1,SI0,L)..0,'T_C'=0..15):T2_T0:=subs(q=q2_,dat2,dat,SI0,T_T0);pl2:=plot([seq(subs(t=10*i,T2_T0),i=1..10)],x=0..subs(dat2,SI0,L),'T_C'=0..15):display({pl1,pl2});T1_T0_100_L:=evalf(subs(t=100,x=L,dat1,SI0,T1_T0));T1_T0_100_0:=evalf(subs(t=100,x=1e-9,T1_T0));T2_T0_100_0:=evalf(subs(t=100,x=1e-9,T2_T0));T2_T0_100_L:=evalf(subs(t=100,x=L,dat2,SI0,T2_T0)); |
 |
|
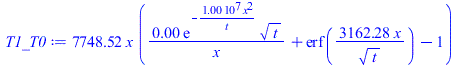 |
|
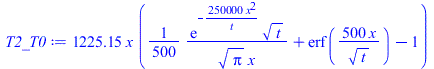 |
|
 |
|
| (4) |
i.e., con el modelo doblemente semi-infinito, al cabo de 100 s se alcanza una Tmax-T0=13.8 ºC (en el calefactor), con calentamientos en los extremos de T2-T0=4,9 ºC a la izquierda de la placa 1, y T1-T0=0,5 ºC a la derecha de la placa 2, mientras que con el modelo de bordes aislados era Tmax-T0=15,2 ºC, T2-T0=9,7 ºC y T1-T0=1,3 ºC. Nótese que todo se calienta más en el caso de bordes aislados, pero en el contacto apenas se nota (Tmax-T0=15,2 ºC frente a 13,8 ºC), mientras que en los bordes la diferencia es mucho mayor (e.g. a la derecha de la placa 2 es T2-T0=9,7 ºC frente a los T1-T0=4,9 ºC del modelo semi-infinito).
e) Evolución T(x,t) si se apaga el calentador tras 100 s de funcionamiento.
Resuelto con Matlab para bordes aislados.
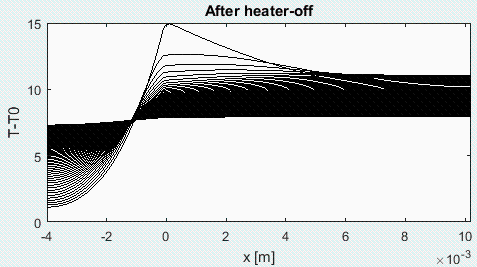
i.e. si los extremos están aislados, toda la energía queda almacenada en las placas, que adquieren una temperatura uniforme de Tmean-T0=Q*Dt/(mc)=8 ºC (nótese la rapidez conque se amortigua el pico en el contacto, x=0).
En realidad (y con el modelo semiinfinito) toda la energía se disipará y las placas quedarían a la T inicial.
f) Estimación de las pérdidas laterales en las placas, debido al menor tamaño del calentador.
En el caso más desfavorable (más caliente), la placa 1 tiene una temperatura media en sus 4 mm de espesor de unos 5 ºC sobre la Tb=0 ºC, y la placa 2 de unos 12 ºC sobre la Tb. Pero esto es solo un modelo 1D que será muy bueno en el centro del calentador de 0,1·0,1 m2, pero irá perdiendo validez a medida que nos alejemos a lo largo del eje y (o z). Una estimación de las pérdidas de calor en esa dirección es (tomando como longitud característica Lh=longitud del heater):
| > | Qy:=k*Ay*(Tm-T0)/Lh;Ay=Lh*L;Lh_:=subs(dat,SI0,sqrt(A))*m_;Ay1_:=subs(dat1,Lh_*L);'Ay1_'=%*1e6*mm_^2/m_^2;Ay2_:=subs(dat2,Lh_*L);'Ay2_'=%*1e6*mm_^2/m_^2;;Tm1:=5*K_+T0;Qy1_:=subs(dat1,dat,k*Ay1_*(Tm1-T0)/Lh_);Tm2:=T0+12*K_;Qy2_:=subs(dat2,dat,k*Ay2_*(Tm2-T0)/Lh_);Qlost:=4*(Qy1+Qy2);Qlost_:=4*(Qy1_+Qy2_); |
| (5) |
i.e. el modelo 1D era muy bueno ya que las pérdidas laterales (sumando ambas placas y contando con las 4 direcciones), apenas son de 0,5 W frente a las 20 W del calentador. Nótese que casi todas las pérdidas laterales son debidas a la placa 2 porque se calienta más.
| > |