| > | restart:#"m11_p88" |
Considérese una chapa de acero inoxidable SS-340 de 10 mm de espesor, inicialmente a 300 K, que va a ser expuesta a una radiación frontal de 100 W/cm2. Se pide:
a) Estimar el tiempo que tardaría en fundirse la chapa suponiendo difusividad térmica infinita.
b) Estimar el tiempo que tardaría en fundirse la superficie suponiendo espesor infinito.
c) Estimar la velocidad de ablación.
d) Determinar el perfil de temperatura con ablación suponiendo espesor infinito.
Datos:
| > | read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):with(plots): |
| > | su:="Acero_inox":dat:=[delta=1e-2*m_,q=1e6*W_/m_^2,T0=300*K_];datSS:=get_sol_data(su),T[b]=3000*K_,h[sl]=280e3*J_/kg_,h[lv]=6300e3*J_/kg_;dat:=op(dat),datSS,Const,SI2,SI1:eqa:=a=k/(rho*c);eqa_:=subs(dat,%);%*1e6; |
| (1) |
a) Estimar el tiempo que tardaría en fundirse la chapa suponiendo difusividad térmica infinita.
Para empezar, habría que detallar más esa radiación. Aquí vamos a suponer que ese valor corresponde ya al intercambio neto radiativo, porque si no habría que saber qué parte de la radiación incidente es absorbida por el acero y cuánto emite éste hacia delante (que dependerá de su emisividad) y de la temperatura aparente de lo que tenga enfrente. Nótese que un cuerpo negro a 3000 K en un ambiente a 300 K ya pierde q=sigma*(T3000^4-T300^4)=4,6 MW/m2. Y la emisividad del SS304 a 3000 K es ya casi 0,4 (aumenta con la temperatura). La absortancia dependerá de la longitud de onda de la radiación incidente.
| > | eqBE:=m*(c*DT+h[sl])=Q*Dt;Dt_bulk:=rho*delta*(c*(T[f]-T0)+h[sl])/q;Dt_bulk_:=subs(datSS,dat,%);Dt_bulk_ini:=rho*delta*(c*(T[f]-T0))/q;Dt_bulk_ini_:=subs(datSS,dat,%); |
| (2) |
i.e. si el calentamiento fuese uniforme en todo el espesor, tardaría 55 s en empezar a fundir, y 77 s en estar todo fundido.
b) Estimar el tiempo que tardaría en fundirse la superficie suponiendo espesor infinito.
La solución al problema de deposición continua en la superficie de un medio semiinfinito es conocida; se trata de una solución de semejanza en la variable eta, con la función Eta(eta) representada en la figura (comprobamos que en x=0 se cumple q=-k*dT/dx).
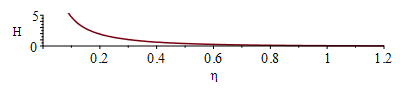
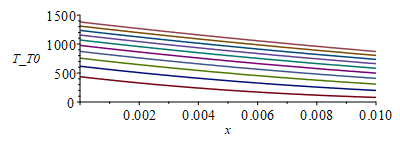
| > | eqT:=T(x,t)-T0=(q*x/k)*Eta;Eta:=exp(-eta^2)/(sqrt(Pi)*eta)+erf(eta)-1;eqeta:=eta=x/sqrt(4*a*t);eqT0:=T(0,t)-T0=2*q*sqrt(t/(Pi*rho*c*k));plot(Eta,eta=0..1.2,'Eta'=0..5);eqT_:=subs(eqeta,eqT):eqTp:=dT/dx=diff(rhs(eqT_),x):eqTp0:=(dT/dx)[x=0]=convert(series(rhs(eqTp),x=0,2),polynom);T_T0:=subs(eqeta,rhs(eqT));T_T0_:=subs(eqa_,datSS,dat,SI0,T_T0);pl2:=plot([seq(subs(t=10*i,T_T0_),i=1..10)],x=0..subs(dat,SI0,delta),'T_T0'=0..1500);plot(subs(datSS,dat,SI0,rhs(eqT0)),t=0..100,To_T0=0..1500); |
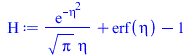 |
|
 |
|
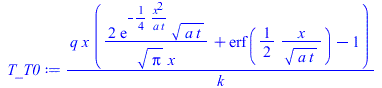 |
|
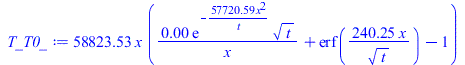 |
|
 |
|
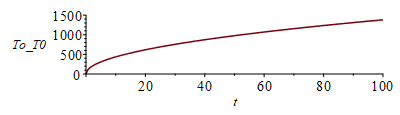 |
En el gráfico T(x,t)-T0 se ve el calentamiento en todo el espesor, i.e. T(x) cada 10 s. Se ve que ya en los primeros 10 s el calentamiento ha llegado al otro lado de la chapa. También se aprecia que al cabo de 100 s ya se ha alcanzado la fusión en la cara irradiada, Tf_T0=1700-300=1400 K. Podríamos haber estimado el tiempo de penetración del calor por difusión como Dt=L^2/a=0,01^2/4e-6=25 s.
En el gráfico T(0,t)-T0 se ve cómo se calienta la superficie. Vemos que con este modelo semiinfinito la superficie irradiada tardaría unos 100 s en empezar a fundirse, mientras que con el modelo anterior en 55 s ya habría empezado a fundir la chapa completa, lo que es una inconsistencia. La explicación de que con el modelo semiinfinito tarde más es que con este modelo se pierde mucho calor por conducción hacia la derecha de x=0,01 m, que con el primer modelo no se contabilizaba. En la realidad, dependerá de la condición térmica en el envés de la chapa, que si está al aire se parecerá al caso adiabático.
c) Estimar la velocidad de ablación.
Si se mantiene la irradiación, el acero empezará a fundir y luego a vaporizarse, desapareciendo masa de la cara irradiada (ablación). Primero estimaremos el tiempo que tardaría en empezar la vaporización, i.e. en llegar a la temperatura de ebullición del acero, y la velocidad de ablación 'va' si todo el flujo q=1 MW/m2 se invirtiera en vaporizar el acero (sin pasar nada por conducción hacia dentro).
| > | eqBEunsteady:=m*(c*(T[f]-T0)+h[sl]+c[L]*(T[b]-T[f]))=Q*Dt;Dt_bulk_boil:=rho*delta*(c*(T[f]-T0)+h[sl]+c[L]*(T[b]-T[f]))/q;Dt_bulk_boil_:=subs(c[L]=c,datSS,dat,%);eqBEsteady:=va*rho*Dh=q;va_:=q/(rho*Dh);Dh:=c*(T[f]-T0)+h[sl]+c[L]*(T[b]-T[f]);va__:=subs(eqa_,c[L]=c,datSS,dat,va_)*1e3*mm_/m_; |
| (3) |
i.e. a partir de unos 130 s ya empezaría la ablación (se ha tomado c_liq=c_sol por falta de datos), y esta avanzaría (comiendo material) a 0,08 mm/s, por lo que en unos 10/0,08=125 s habría desaparecido la chapa. Nótese que ambos tiempos son iguales, pues si toda la chapa se calienta uniformemente hasta ebullición, desaparecería toda a la vez.
d) Determinar el perfil de temperatura con ablación suponiendo espesor infinito.
No podemos usar el modelo de conducción en medio semiinfinito con una parte fundida por la absorción de calor en la interfase líquido-sólido (daría lugar a un problema de Stefan).
Analizando ya el problema de ablación en régimen estacionario, en ejes móviles, i.e. con el origen x=0 en el frente de ablación moviéndose a velocidad va, consideraremos un sumidero térmico ablativo superficial de intensidad qa, algo menor que la entrada q=1 MW/m2, pues la diferencia será lo que se trasmite por conducción hacia dentro del material, qc, y la expresión de este último para el caso semiinfinito que viene en Heat source moving at steady state along a rod, tenemos:
| > | eqBEsup:=q=qa+qc;q=subs(dat,q);eqqa:=qa=va*rho*(c*(T[f]-T0)+h[sl]+c[L]*(T[b]-T[f]));eqqc:=qc=k*(T[b]-T0)*va/(2*a);va_:=solve(subs(eqqa,eqqc,eqBEsup),va);va__:=subs(eqa_,c[L]=c,datSS,dat,%);va=%*1e3*mm_/m_;qa_:=subs(va=va__,eqa_,c[L]=c,datSS,dat,rhs(eqqa));qc_:=subs(va=va__,eqa_,c[L]=c,datSS,dat,rhs(eqqc)); |
| (4) |
i.e. el frente ablativo se mueve a 0,06 mm/s, disipando 0,7 MW/m2 por ablación y transmitiendo los 0,3 MW/m2 restantes por conducción hacia dentro, todo ello con este modelo semiinfinito, con el cual el perfil de temperaturas (estacionario en ejes móviles) sería (tomado de la referencia anterior) y solo para la parte sólida:
| > | eqT:=T(x)-T0=(T[f]-T0)*exp(-va*x/a);plot(subs(eqa_,va=va__,datSS,dat,SI0,rhs(eqT)),x=0..subs(dat,SI0,delta),'T_T0'=0..1500); |
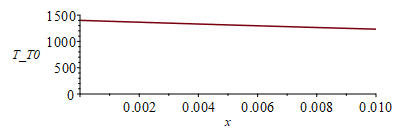 |
Otra vez vemos que el modelo semiinfinito no es apropiado para 10 mm de acero y tiempos grandes (el flujo conductivo no sería tan grande al no haber material después de x=0,01 m, y por tanto la velocidad de ablación sería mayor, acercándose al valor máximo de qc=0 que será va*q/qa=0,06·1/0,7=0,09 mm/s).
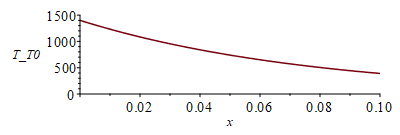
Si se resuelve el problema para 10 cm de acero en vez de 1 cm, los perfiles transitorios y el estacionario ablativo serían estos de abajo (se ve que el transitorio ya vale, pero el estacionario todavía necesitaría más espesor):
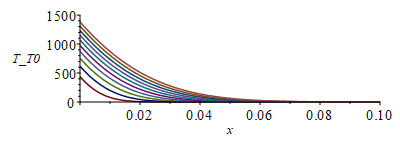
Este ejercicio podría servir para estudiar el efecto de un haz de láser potente sobre una chapa de acero.
Los escudos ablativos que se usan para proteger del plasma que se forma en la reentrada de vehículos en atmósferas planetarias no son de metal sino de materiales compuestos de epoxi y fibra de vidrio, de mucha menor densidad y menor conductividad térmica que el acero, y su ablación lleva consigo reacciones químicas, además de los procesos físicos aquí considerados; estos escudos pueden ser de más de 40 mm de espesor, aunque solo se llega a quemar unos 15 mm.

Fig. 1. Ensamblaje del escudo ablativo de la cápsula Dragon de SpaceX.
| > |