| > | restart:#"m11_p87" |
Considérese un tanque cilíndrico de propano, de 1 m de diámetro y 3 m de longitud, enterrado bajo 1 m de arena. Determinar el flujo máximo de gas suministrable (o de pérdidas por fisuras).
| > | with(RealDomain):read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc): |
| > | su1:="C3H8":su2:="Arena":dat:=[D=1*m_,L=3*m_,H=1*m_];datP:=get_liq_data(su1);get_sol_data(su2):dat:=k=subs(%,k),op(dat),Const,SI2,SI1:k[arena]=subs(%,k);get_pv_data(su1): |
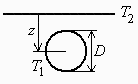
Como el propano se almacena líquido (GLP), al ir saliendo gas se irá reponiendo con la vaporización de líquido, pero como esto requiere un aporte de energía para compensar la entalpía de cambio de fase, el gasto suministrable viene limitado por el flujo de calor entrante, que para un depósito enterrado será por conducción desde la superficie.
Si suponemos que inicialmete está todo atemperado a unos 15 ºC, al empezar a salir gas se irá enfriando (y disminuyendo la presión interior), hasta llegar al equilibrio energético. Si despreciamos la pérdida de presión del gas en el conducto de salida ( o a través de las fisuras), el flujo máximo tendrá lugar cuando el salto térmico sea máximo, l cual implica que el GLP se enfría hasta que la presión interior sea la atmosférica.
Sea 1 las condiciones atmosféricas (100 kPa y 15 ºC), y 2 las condiciones de enfriamiento máximo del depósito (100 kPa, Tb):
| > | eqQmax:=T2=T[b];eqQmax:=T2=subs(datP,T[b]);Tini_:=subs(dat,T0);p_ini_:=pv(Tini_); |
| (1) |
i.e. si la Tinicial=15 ºC, el tanque de propano bifásico estaría a 725 kPa, y cuendo sale gas a flujo máximo su temperatura ha bajado a 231 K (-42 ºC).
El flujo de calor desde la superficie al tanque es difícil de calcular en el caso tridimensional, pero si despreciamos los efectos de los extremos, el caso bidimensional viene resuelto con la fórmula del factor de forma para conducción, de la Tabla 1, válido para L/R>>1. En nuestro caso, L/R=3/0,5=6, y z=H+D/2).
| > | eqQ:=Q=k*S*(T1-T2);eqS:=S=2*Pi*L/arccosh(2*z/D);z:=H+D/2;z_:=subs(dat,%);T1=Tini_;T2=rhs(eqQmax);eqS_:=evalf(subs(dat,eqS));eqQ_:=subs(dat,evalf(subs(eqS,T1=T0,T2=rhs(eqQmax),dat,eqQ))); |
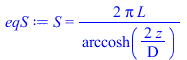 |
|
| (2) |
i.e. el tanque recibe 366 W desde el ambiente, por lo que el flujo vaporizable es:
| > | eqmmax:=m=Q/h[lv0];h[lv0]=subs(datP,h[lv0]);eqmmax_:=subs(eqQ_,datP,dat,eqmmax);m=rhs(%)*3600*s_/h_; |
| (3) |
i.e. unos 3 kg/h es la cantidad máxima obtenible de propano del depósito enterrado, ya sea por tubería o por fugas.
La conductividad térmica del terreno depende de la composición y textura del suelo; aumenta con la densidad y el contenido de agua, y disminuye con el contenido de materia orgánica. De ser arena a ser tierra puede ser el doble de k (y por tanto el doble de flujo).
| > |