>	restart:#"m11_p86"

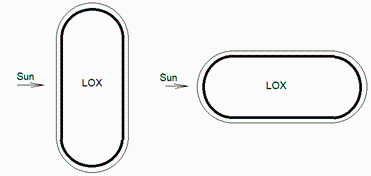
Considérese un depósito de oxígeno líquido (LOX) a 250 kPa, en el espacio, a una distancia del Sol de 1,01 ua (órbita halo en L2). Aunque se prevé disponer un parasol, se quiere estudiar el caso en que recibiera el sol perpendicular al eje del tanque, que es cilíndrico rematado en semiesferas, de 2 m de diámetro exterior y 5 m de longitud total. La pared del tanque en contacto con el líquido (que se supondrá isotermo), es de 2 mm de Al-7075 (k=100 W/(m·K) a 100 K), y está recubierta de una capa de 50 mm de espesor de espuma de poliuretano (=50 kg/m3 y k=0.007 W/(m·K) en vacío a 100 K), con acabado reflectante solar de propiedades =0,1 y =0,8. Se pide:
a) Calcula con un modelo 1D de pared plana enfrentada al Sol, el perfil de temperatura a través de la pared, y el flujo de calor entrante. Sol.: Text=180 K.
b) Calcula con un modelo 1D de pared plana enfrentada al vacío interplanetario, el perfil de temperatura a través de la pared, y el flujo de calor saliente.
c) Calcular con un modelo cilíndrico 2D cuasi-1D (sin conducción azimutal) la variación azimutal de la temperatura exterior, y el calor neto intercambiado despreciando los extremos esféricos.
d) Calcular con un modelo esférico 2D cuasi-1D (sin conducción azimutal) la variación azimutal de la temperatura exterior de cada casquete, en el caso de insolación axial, y el calor neto intercambiado en este caso por todo el tanque.
Datos:

>	with(RealDomain):read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):assume(h_>0,r>0):

>	su:="O2":dat:=[p0=250e3*Pa_,Rst_ua=1.01,R=1*m_,L=5*m_,delta0=2e-3*m_,k0=100*W_/(m_*K_),delta1=0.05*m_,k1=0.007*W_/(m_*K_),alpha=0.1,epsilon=0.8,Tinf=2.7*K_,E0=1360*W_/m_^2,e=0.017];dat:=op(dat),Const,SI2,SI1:Odat:=get_liq_data(su),get_gas_data(su);get_pv_data(su):

a) Calcula con un modelo 1D de pared plana enfrentada al Sol, el perfil de temperatura a través de la pared, y el flujo de calor entrante.

Lo primero será saber la temperatura interior, T_LOX a 250 kPa. El ELV con la ecuación de Antoine es:

>	eq6_41;eq6_42;T0_:=evalf(subs(dat,solve(p0=pv(T),T)));

	(1)

i.e. la TLOX=100 K, que será prácticamente la T interior del aislante, puesto que la pared de aluminio apenas tiene resistencia térmica.  

>	eqRt:=Rt=DT/Q;eqRt:=Rt=delta/(k*A);eqrt:=rt=delta/k;rt_Alu:=subs(dat,delta0/k0);rt_Ais:=subs(dat,delta1/k1);

	(2)

Lo segundo será saber la temperatura exterior, que vendrá determinado por el balance energético en la superficie (absorción solar = emisión IR + flujo hacia dentro).

>

eqBE:=Qs=Qinf+Qcond;eqqs:=Qs/A=alpha*E;eqE:=E=E0/((1-e)*Rst_ua)^2;E_:=subs(dat,rhs(%));eqqs_:=subs(E=E_,dat,eqqs);eqqinf:=Qinf/A=epsilon*sigma*T1^4;eqqcond:=Qcond/A=k1*(T1-T0)/delta1;eqBE_:=subs(T0=T0_,dat,SI0,rhs(eqqs_)=rhs(eqqinf)+rhs(eqqcond));T1_:=fsolve(%,T1=10..500)*K_;'T1_'=TKC(%);Qinf_:=subs(T1=T1_,dat,SI0,rhs(eqqinf))*W_/m_^2;Qcond_:=subs(T0=T0_,T1=T1_,dat,SI0,rhs(eqqcond))*W_/m_^2;T1max:=T1_;Qmax:=Qcond_;

	(3)

i.e. el exterior quedaría a 238 K, absorbiendo 138 W/m2 solar, emitiendo 120 W/m2 de IR al espacio vacío, y transmitiendo 18 W/m2 hacia dentro, al LOX.

b) Calcula con un modelo 1D de pared plana enfrentada al vacío interplanetario, el perfil de temperatura a través de la pared, y el flujo de calor saliente.

Ahora el balance en la superficie externa será entre lo que recibe del LOX y lo que evacúa al vacío a 2,7 K.

>	eqBE:=Qcond=Qinf;eqBE_:=-rhs(eqqcond)=rhs(eqqinf);T1_:=fsolve(subs(T0=T0_,dat,SI0,%),T1=1..100)*K_;'T1_'=TKC(%);qinf_:=subs(T1=T1_,dat,SI0,rhs(eqqinf))*W_/m_^2;qcond_:=subs(T0=T0_,T1=T1_,dat,SI0,-rhs(eqqcond))*W_/m_^2;

	(4)

i.e. enfrentado al vacío a Tinf=2,7 K, el exterior queda a 84 K, recibiendo 2,2 W/m2 del interior (LOX) y emitiéndolos al espacio.

c) Calcular con un modelo cilíndrico 2D cuasi-1D (sin conducción azimutal) la variación azimutal de la temperatura exterior, y el calor neto intercambiado despreciando los extremos esféricos.
Sin conducción azimutal basta tener en cuenta que el sol no da de plano en la cara iluminada sino en función del coseno (modelo de rayos solares paralelos).

>	eqBE:=Qs=Qinf+Qcond;eqqs:=qs=alpha*E*cos(theta);eqBE_:=qs=rhs(eqqinf)+rhs(eqqcond);eqBE__:=subs(eqqs,T0=T0_,E=E_,dat,SI0,eqBE_);plot(solve(%,T1),theta=0..Pi/2,T1_K=0..225);

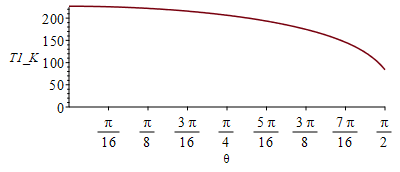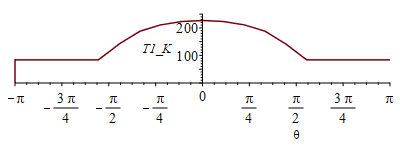
i.e. la T_exterior decae desde los 227 K de la zona que apunta al sol, hasta los 189 K de toda la zona en sombra. Si lo queremos calcular automáticamente en todo el rango:

>

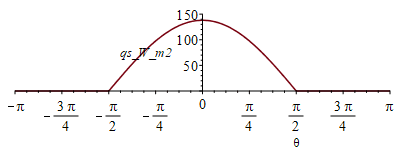
qs_:=piecewise(abs(theta)>Pi/2,0,subs(SI0,rhs(eqqs_)*cos(theta)));plot(qs_,theta=-Pi..Pi,qs_W_m2=0..150);N:=9;pl:=[[-Pi,0]]: for i from -N to N do eqBE__:=subs(T0=T0_,E=E_,dat,SI0,subs(theta=Pi*i/N,qs_)=rhs(eqqinf)+rhs(eqqcond));sol:=max(solve(%,T1));pl:=[op(pl),[Pi*i/N,sol]];od:plot(pl,theta=-Pi..Pi,T1_K=0..250);

>

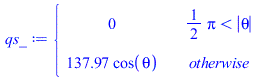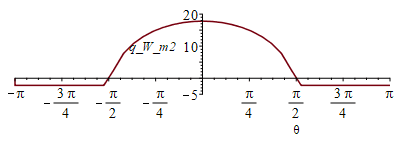
Qcyl:=Int(qcond*R*Lcyl,theta=-Pi..Pi);Qcyl:=Qcyl_sol+Qcyl_umb;Qcyl_sol:=2*Int(k1*R*Lcyl*(T1-T0)/delta1,theta=0..Pi/2);Qcyl_umb:=k1*Lcyl*R*Pi*(T1-T0)/delta1;Lcyl:=L-2*R;Lcyl_:=subs(dat,%);Qcyl_umb_:=subs(T0=T0_,T1=T1_,dat,Qcyl_umb);N:=19;pl:=[[-Pi,0]]: Qcyl_:=0:for i from -N to N do eqBE__:=subs(T0=T0_,E=E_,dat,SI0,subs(theta=Pi*i/N,qs_)=rhs(eqqinf)+rhs(eqqcond));sol:=max(solve(%,T1));q:=subs(dat,SI0,k1*(sol-T0_)/delta1);pl:=[op(pl),[Pi*i/N,q]];Qcyl_:=Qcyl_+subs(dat,SI0,q*R*Lcyl*Pi/N);od:plot(pl,theta=-Pi..Pi,q_W_m2=-5..20);Qcyl:=Qcyl_*W_;

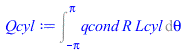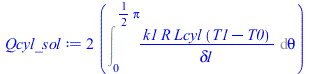	(5)

i.e. por el lateral del cilindro entran 102 W netos (entran 123 W por la zona soleada y salen 21 W por la umbría. Como comprobación, podemos aproximar a entrada uniforme por la cara iluminada, que a qmax=18 W/m2 hacen qmax·2RLcyl=18·2·1·3=108 W, menos los que salen por detrás, que a razón de qmin=2,2 W/m2 son qmin·Pi*R*Lcyl=2,2·3·1·3=20 W, luego, el orden de magnitud es correcto.

d) Calcular con un modelo esférico 2D cuasi-1D (sin conducción azimutal) la variación azimutal de la temperatura exterior de cada casquete, en el caso de insolación axial, y el calor neto.ç

Si el sol no da perpendicular al eje del depósito sino alineado con él, quedará iluminado solo un casquete (suponiendo rayos paralelos).

La distribución de temperaturas y flujos de calor será análoga al caso cilíndrico, con una T1_max=227 K y una T1_min=84 K, como antes, y unos flujos de calor qmax=18 W/m2 y qmin=-2,2 W/m2, olo que ahora está soleado un casquete, y a la sombra todo el lateral y el otro casquete.

Con el modelo aproximado de tomar el flujo uniforme en el casquete soleado, Qin=qmax·Pi·R2=18·3·1=54 W, y Qout=qmin·(2·Pi·R^2+2·Pi·R·Lcyl)=2,2·(2·3·1+2·3·1·3)=2,2·24=53 W, luego el calor neto entrante al LOX será del orden de 54-53=1 W. ¡Vaya! resultan demasiado parecidos para que sea buena la estimación.

El cálculo exacto del calor que entra por el casquete soleado es:

>

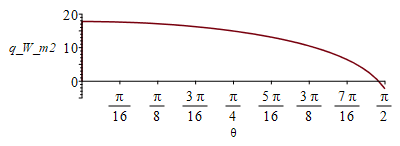
Qsph_sol:=Int(k*2*Pi*R*sin(theta)*R*(T1(theta)-T0)/delta1,theta=0..Pi/2);N:=39; Qsph_:=0:pl:=[[0,0]]:for i from 0 to N do theta_:=evalf((Pi/2)*i/N);eqBE__:=subs(T0=T0_,E=E_,dat,SI0,subs(theta=theta_,qs_)=rhs(eqqinf)+rhs(eqqcond));T1__:=max(solve(%,T1));q:=subs(dat,SI0,k1*(T1__-T0_)/delta1);pl:=[op(pl),[theta_,q]];Qsph_:=Qsph_+subs(dat,SI0,q*2*Pi*R*sin(theta_)*R*Pi/(2*N));od:plot(pl,theta=0..Pi/2,q_W_m2=-5..20);Qsph_sol:=evalf(Qsph_)*W_;Qsph_umb:=subs(dat,evalf(subs(dat,-qinf_*(2*Pi*R*Lcyl_+2*Pi*R^2))));Qsph:=Qsph_sol+Qsph_umb;

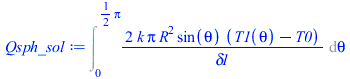	(6)

i.e. la entrada por el casqute iluminado era de 70 W (en vez de los 54 W estimados), con lo que el neto será 70-56=13,6 W (en vez de 1 W estimado).

Aunque esta entrada neta de calor pueda parecer pequeña, si tenemos en cuenta que la entalpía de vaporización del LOX a 100 K es hlv=203 kJ/kg (hlv=213 kJ/kg a Tb=90 K), la cantidad de oxígeno que se perdería para que no aumentase la presión sería m_vap=Q/hlv=13,6/203=0,067 g/s=5,8 kg/día. Y un orden de magnitud más si el sol le diera perpendicularmente.

>