| > | restart:#'m11_p85' |
| > | read"../therm_eq.m":read"../therm_proc.m":with(therm_proc): |
Un modelo térmico preliminar de un sensor activo montado exteriormente en un satélite, consiste en una esfera de 5 cm de diámetro y capacidad térmica despreciable, mantenida a 1 m de distancia del satélite mediante un tubo telescópico de aluminio de 1 cm de diámetro y 1 mm de espesor. Se quiere estudiar el perfil de temperatura a lo largo del tubo cuando en la esfera se disipan 10 W, suponiendo ésta isoterma, y el encastre con el satélite a 20 ºC. En particular, se pide:
a) Para un ensayo térmico en tierra en una sala con aire a 20 ºC, determinar analíticamente el perfil de temperatura en régimen estacionario suponiendo un coeficiente convectivo con el aire exterior de 5 W/(m2·K).
b) Determinar numéricamente el transitorio cuando se conecta el sensor estando todo inicialmente a temperatura ambiente.
c) Ya en el espacio, calcular la temperatura que alcanzaría la esfera en presencia de la radiación de fondo del universo solamente, y en el caso de estar también expuesta al sol.
d) Determinar el perfil de temperatura a lo largo del tubo en régimen estacionario en el espacio, despreciando el acoplamiento radiativo con el resto del satélite.
Data:
Se van a tomar estos datos termo-ópticos para la superficie del tubo de alumnio, aunque dependen mucho del tratamiento supercicial.
| > | dat:=D=0.05*m_,L=1*m_,d=0.01*m_,delta=1e-3*m_,Wdis=10*W_,T0=(20+273.15)*K_,Ta=(20+273.15)*K_,h=5*W_/(m_^2*K_),E=1360*W_/m_^2;su:="Aluminio_anodizado";dat:=dat,get_sol_data(su),Const,SI2,SI1:alpha=subs(dat,alpha);epsilon=subs(dat,epsilon);unprotect(D): |
| (1) |

a) Para un ensayo térmico en tierra en una sala con aire a 20 ºC, determinar analíticamente el perfil de temperatura en régimen estacionario suponiendo un coeficiente convectivo de 10 W/(m2·K).
El balance energético de un elemento diferencial de varilla, despreciando los acoplamientos térmicos por el interior hueco del tubo, es:
| > | eqBE:=m*c*dT/dt=Qin-Qout;eqBE:=As*dx*rho*c*dT/dt=-(k*As*dT/dx)[x+dx]+(k*As*dT/dx)[x]-Pi*d*dx*h*(T-Ta);As:=Pi*d*delta;As_:=subs(dat,%):'As'=%*1e6*mm_^2/m_^2;As:=Pi*(d^2-(d-2*delta)^2)/4;As_:=subs(dat,%);'As'=%*1e6*mm_^2/m_^2;eqBE:=rho*c*Diff(T,t)=k*Diff(T,x,x)-Pi*d*h*(T-Ta)/As;eqBEst:=0=diff(T(x),x,x)-Pi*d*h*(T(x)-Ta)/(k*As);eqCC0:=T(0)=T0;eqCC1:=k*'As'*diff(T(x),x)[x=L]=Wdis-Qe;eqQe:=Qe=Pi*D^2*h*(Te-Ta); |
| (2) |
siendo As el área de la sección del material (nótese que la aproximación de pared delgada daría un 10 % más de área), eqCC las condiciones de contorno, y Qe el calor evacuado por convección en la propia esfera, que dependerá de la temperatura de la esfera, Te (el resto hasta los 10 W saldrá por conducción al tubo). Nótese que para la convección se toma toda el área de la esfera sin restarle la unión con el tubo.
La solución será una combinación de la solución en el tubo (caso 2 de la Tabla 4 de Conducción) y de la pérdida en la esfera:
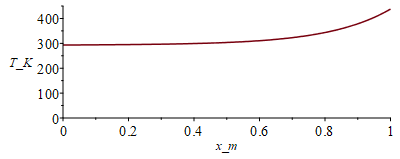
| > | eqTt:=(Tt(x)-Ta)/(Te-Ta)=sinh(m*x)/sinh(m*L);eqQtL:=QtL/((Te-Ta)*sqrt(p*h*k*As))=1/tanh(m*L);eqm:=m=sqrt(h*p/(k*A));p=Pi*d;eqm:=m=sqrt(h*Pi*d/(k*As));eqm_:=evalf(subs(dat,%));QtL_:=solve(subs(eqm_,p=Pi*d,A=As,dat,SI0,eqQtL),QtL);Qe_:=subs(dat,SI0,rhs(eqQe));eqBEe:=Wdis=QtL+Qe;eqBEe:=subs(dat,SI0,Wdis=QtL_+Qe_);Te_:=solve(%,Te)*K_;'Te_'=TKC(%);QtL__:=subs(Te=Te_,SI0,QtL_)*W_;Qe__:=subs(Te=Te_,SI0,Qe_)*W_;plot(subs(x=x_m,Te=Te_,eqm_,dat,SI0,Ta+(Te-Ta)*rhs(eqTt)),x_m=0..subs(dat,SI0,L),T_K=0..450);plot(subs(x=x_m,Te=Te_,eqm_,dat,SI0,Ta-273.15+(Te-Ta)*rhs(eqTt)),x_m=0..subs(dat,SI0,L),T_C=0..200);eqAt:=At=Pi*d*L;eqAt_:=subs(dat,%);eqAe:=Ae=Pi*D^2;eqAe_:=subs(dat,%);eq:=At/Ae=rhs(eqAt_)/rhs(eqAe_); |
 |
|
 |
|
| (3) |
i.e. la esfera queda a Te=165 ºC, y el tubo adquiere la T(x) graficada; nótese que casi la mitad de la varilla permanece a 20 ºC (sólo se calienta el extremo cercano a la esfera). Puede sorprender que de los 10 W que disipa la esfera, salgan más directamente por convección al aire (Qe=5,7 W) que por conducción al tubo de aluminio en su unión (Qt=4,3 W), y de ahí por convección al aire a lo largo de toda el área del tubo, que es 4 veces mayor que la de la esfera, pero la explicación es que la esfera está a la máxima temperatura, y el tubo está relativamente frío, como se aprecia en la gráfica. Por cierto, que no parece muy razonable haber supuesto que la capacidad térmica de la esfera es despreciable (aparte de la pared, habría que saber la capacidad térmica de los equipos que disipan esos 10 W).
También se podría haber resuelto la EDO directamente por Maple:
| > | eqs:=eqBEst,T(0)=T0,D(T)(L)=(Wdis-Pi*D^2*h*(T(L)-Ta))/(k*As);sol:=dsolve({eqs},T(x)):sol_:=evalf(subs(dat,SI0,sol));Tmax_:=evalf(subs(x=L,dat,SI0,rhs(%)))*K_;'Tmax_'=TKC(%); |
| (4) |
b) Determinar numéricamente el transitorio cuando se conecta el sensor estando todo inicialmente a temperatura ambiente.
Solución numérica. Sea N el número de tramos en que dividimos el tubo (N+1 puntos): 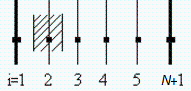 .
.
Como no conocemos la capacidad térmica de la esfera, vamos a suponer que es despreciable frente a la del tubo (ya el área lateral de éste es 4 veces mayor que la superficie de la esfera). En todo caso, el efecto de la capacidad térmica de la esfera solo retardaría el transitorio del tubo, pero no la temperatura final.
El modelo explícito por diferencias finitas 1D, teniendo en cuenta la condición de contorno especial en el extremo, es:
eq11_24_0_;eq11_24_gen_;eq11_24_N_:T:='T':eq0:=subs(epsilon[lat]=0,E0=0,h0=0,h[lat]=h,epsilon0=0,phi=0,eq11_24_0_);eqi:=subs(epsilon[lat]=0,h[lat]=h,phi=0,epsilon0=0,eq11_24_gen_);eqN:=k*A*(T[N+1,j]-T[N,j])/Dx=Wdis-Pi*D^2*h*(T[N+1]-Ta);
![T[i, `+`(j, 1)] = `+`(T[i, j], `*`(Fo, `*`(`+`(T[`+`(i, 1), j], `-`(`*`(2, `*`(T[i, j]))), T[`+`(i, `-`(1)), j]))), `/`(`*`(phi, `*`(Dt)), `*`(rho, `*`(c))), `-`(`/`(`*`(p, `*`(Dt, `*`(`+`(`*`(h[lat],...](images/p851_45.gif) |
|
| (5) |
El tiempo característico para llegar al estado estacionario puede estimarse con la transmitancia térmica transversal (por convección), que es más efectiva que la axial (por conducción), debido a las distancias relativas para el flujo de calor. El espesor que se calienta/enfría es delta=1 mm.
| > | tc:=rho*c*delta/h;tc_:=subs(dat,%); |
| (6) |
i.e. del orden de 500 s. Empezaremos tomando un tiempo de simulación de 1000 s y veremos si es suficiente. Con estos valores la solución es:
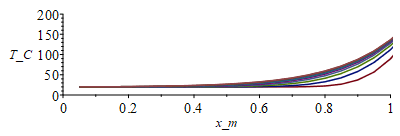
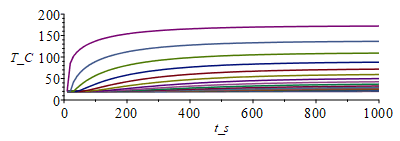
| > | o:=273.15:T:='T':N:=20;Dx:=evalf(subs(dat,SI0,L/N));tsim:=1000;M:=100;Dt:=tsim/M;eqFo:=Fo=k*'Dt'/(rho*c*Dx^2);Fo:=subs(dat,SI0,rhs(%));p_:=subs(dat,SI0,Pi*d);h_:=subs(dat,SI0,h);k_:=subs(dat,SI0,k);rho_:=subs(dat,SI0,rho);c_:=subs(dat,SI0,c);A_:=subs(dat,SI0,As_);T0_:=subs(dat,SI0,Ta);D_:=subs(dat,SI0,D);Wdis_:=subs(dat,SI0,Wdis);T:=Matrix(1..M,1..N+1,T0_):for j from 1 to M-1 do T[j+1,1]:=T0_;for i from 2 to N do T[j+1,i]:=T[j,i]+Fo*(T[j,i-1]-2*T[j,i]+T[j,i+1])+0*phi*Dt/(rho*c)-p_*Dt*h_*(T[j,i]-T0_)/(rho_*c_*A_);od: T[j+1,N+1]:=(T[j+1,N]*k_*A_/Dx+Wdis_+Pi*D_^2*h_*T0_)/(k_*A_/Dx+Pi*D_^2*h_);od:i:='i':j:='j':sx:=seq([seq([i*Dx,T[j_*10,i]-o],i=1..N+1)],j_=1..M/10):plot([sx],x_m=0..1,T_C=0..200);st:=seq([seq([j*Dt,T[j,i]-o],j=1..M)],i=1..N+1):plot([st],t_s=0..tsim,T_C=0..200);Tmax_:=max(T)*K_;'Tmax_'=TKC(%); |
 |
|
 |
|
| (7) |
que concuerda bien con la Tmax obtenida analíticamente (unos 7 K de más, en 438 K para N=20). Vemos que bastar unos 500 s para que el tubo se aproxime al estado estacionario, sin contar la inercia de la esfera, que ampliaría este valor. Podemos estimar el tiempo característico de calentamiento de una esfera de aluminio con el mismo espesor del tubo, desde Ta hasta Tmax y sin pérdidas, tc_cal=Pi*D^2*delta*rho*c*(Tmax-Ta)/Wdis, y el tiempo característico de enfriamiento de la esfera caliente sin potencia disipada ni pérdidas por el tubo, tc_enf=delta*rho*c/h:
| > | T:='T':N:='N':M:='M':tc_cal:=Pi*D^2*delta*rho*c*(Tmax-Ta)/Wdis;tc_cal_:=subs(Tmax=Tmax_,dat,%);tc_enfr:=delta*rho*c/h;tc_enfr_:=subs(dat,%); |
| (8) |
i.e. todos son del mismo orden (y si la esfera fuese más delgada y no metálica todavía sería menor, lo que apoya la suposición de inercia despreciable).
c) Ya en el espacio, calcular la temperatura que alcanzaría la esfera en presencia de la radiación de fondo del universo solamente, y en el caso de estar también expuesta al sol.
Como no se indican las propiedades termoópticas, supondremos que son como las del tubo de aluminio anodizado, aunque es probable que la esfera no sea metálica, así que compararemos con los resultados para cuerpo negro.
| > | eqBE:=Qin=Qout;eqBE:=Wdis+Qs=epsilon*A*sigma*(T^4-Tinf^4);Qs:=alpha*Afrontal*E;eqBE1:=Wdis=epsilon*Pi*D^2*sigma*(T1^4-Tinf^4);T1:=sqrt(sqrt(Wdis/(epsilon*Pi*D^2*sigma)));T1_:=evalf(subs(dat,SI0,%))*K_;'T1_'=TKC(%);T1bb_:=evalf(subs(epsilon=1,alpha=1,dat,SI0,T1))*K_;'T1bb_'=TKC(%);eqBE2:=Wdis+subs(Afrontal=Pi*D^2/4,Qs)=epsilon*Pi*D^2*sigma*(T2^4-Tinf^4);T2:=sqrt(sqrt((Wdis+E*Pi*D^2/4)/(epsilon*Pi*D^2*sigma)));T2_:=evalf(subs(dat,SI0,%))*K_;'T2_'=TKC(%);T2bb_:=evalf(subs(epsilon=1,alpha=1,dat,SI0,T2))*K_;'T2bb_'=TKC(%); |
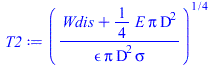 |
|
| (9) |
i.e. sin sol la esfera alcanzaría 136 ºC (114 ºC si emitiera como cuerpo negro), y con sol 161 ºC (138 ºC si cuerpo negro).
d) Determinar el perfil de temperatura a lo largo del tubo en régimen estacionario en el espacio.
Si despreciamos los acoplamientos radiativos del tubo con el cuerpo del satélite y con la esfera, podemos plantear la EDO, pero como es no lineal hay que resolverla numéricamente.
Empezaremos considerando que todo (mástil y esfera) está a la sombra (i.e. sin ganancia solar).
| > | eqBE:='As*dx*rho*c*dT/dt'=-(k*As*dT/dx)[x+dx]+(k*As*dT/dx)[x]-Pi*d*dx*epsilon*sigma*(T^4-Tinf^4);eqBE:=rho*c*Diff(T,t)=k*Diff(T,x,x)-Pi*d*epsilon*sigma*(T^4-Tinf^4)/'As'; |
| (10) |
Las ecuaciones discretizadas son:
| > | N:='N':Fo:='Fo':A:='A':Dt:='Dt':Dx:='Dx':eq0:=subs(epsilon[lat]=epsilon,E0=0,h0=0,h[lat]=0,epsilon0=0,phi=0,eq11_24_0_);eqi:=subs(epsilon[lat]=epsilon,h[lat]=0,phi=0,epsilon0=0,eq11_24_gen_);eqN:=k*A*(T[N+1,j]-T[N,j])/Dx=Wdis-Pi*D^2*epsilon*sigma*(T[N+1]^4-Tinf^4); |
| (11) |
Nótese que ahora esta última ecuación (el acoplamienco con la esfera) es no lineal. La vamos a resolver también numéricamente.
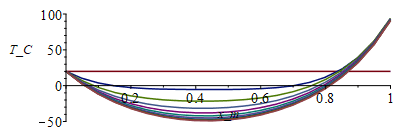
| > | o:=273.15:T:='T':Fo:='Fo':N:=20;Dx:=evalf(subs(dat,SI0,L/N));tsim:=2000;M:=301;Dt:=evalf(tsim/M);eqFo:=Fo=k*'Dt'/(rho*c*Dx^2);Fo:=subs(dat,SI0,rhs(%));p_:=subs(dat,SI0,Pi*d);epsilon_:=subs(dat,SI0,epsilon);sigma_:=subs(dat,SI0,sigma);k_:=subs(dat,SI0,k);rho_:=subs(dat,SI0,rho);c_:=subs(dat,SI0,c);A_:=subs(dat,SI0,As_);T0_:=subs(dat,SI0,Ta);D_:=subs(dat,SI0,D);Wdis_:=subs(dat,SI0,Wdis);T:=Matrix(1..M,1..N+1,T0_):for j from 1 to M-1 do T[j+1,1]:=T0_;for i from 2 to N do T[j+1,i]:=T[j,i]+Fo*(T[j,i-1]-2*T[j,i]+T[j,i+1])-p_*Dt*epsilon_*sigma_*(T[j,i]^4-0)/(rho_*c_*A_);od:eq:=subs(SI0,k_*As_*(Tx-T[j+1,N])/Dx)=Wdis_-Pi*D_^2*epsilon_*sigma_*Tx^4; T[j+1,N+1]:=fsolve(eq,Tx=10..1000);od:i:='i':j:='j':MM:=30:sx:=seq([seq([(i-1)*Dx,T[1+(jm-1)*MM,i]-o],i=1..N+1)],jm=1..(M-1)/MM):plot([sx],x_m=0..1,T_C=-50..100);st:=seq([seq([j*Dt,T[j,i]-o],j=1..M)],i=1..N+1):plot([st],t_s=0..tsim,T_C=-50..100);Tmax_:=max(T)*K_;'Tmax_'=TKC(%);Tmin_:=TKC(min(T)*K_); |
 |
|
 |
|
| (12) |
i.e. como hemos mantenido el perfil inicial T(x)=20 ºC para el tubo, observamos que el tubo comienza a enfriarse por emisión hacia el vacío de fondo (en el caso sin sol), mientras que la esfera (el nodo final) empieza a calentarse immediatamente porque la emisión inicial, que es epsilon*Pi*D^2*sigma*T0^4=2,6 W, es menor que Wdis=10 W. En el estado estacionario, la temperatura del tubo comienza siendo de 20 ºC en el encastre del satélite como se ha impuesto, va bajando conforme se aleja hasta un mínimo de -50 ºC casi a la mitad de la longitud del tubo, y luego va subiendo hasta el máximo de 94 ºC que sería la temperatura de la esfera. Antes se calculó que la esfera sola alcanzaría 136 ºC, pero es que ahora pierde calor por el tubo. Los flujos de calor en los extremos son:
| > | Qt0:=-'k*As*Diff(T,x)[x=0]';Qt0_:=evalf(subs(SI0,-k_*As_*(T[M,2]-T[M,1])/Dx))*W_;QtL:=-'k*As*Diff(T,x)[x=L]';QtL_:=subs(SI0,k_*As_*(T[M,N+1]-T[M,N])/Dx)*W_;T:='T':Qe_94:=epsilon*Pi*D^2*sigma*T94^4;Qe_94_:=subs(T94=Tmax_,dat,%); |
| (13) |
i.e. el tubo extrae 2 W del encastre con el satélite, y 3,8 W de la esfera (la cual emite otros 6,5 W al espacio); nótese la pequeña discrepancia numérica respecto al calor total que sale de la esfera, 10 W: 3,8+6,5=10,3 W.
Respecto a los acoplamientos radiativos, el de los elementos del tubo con la esfera apenas afectará al íltimo elemento (de tamaño Dx=5 cm con N=20, comparable con el tamaño de la esfera, D=5 cm).
Sin embargo, el acoplamiento radiativo entre el tubo y el cuerpo del satélite sí que podría ser importante y, aunque globalmente no lo fuera (e.g. si el tamaño de la cara del satélite fuera también del orden de 1 m, la Tabla: Cylindrical rod to coaxial disc at one end enseña que solo el 15 % de lo que emite un tubo de H=1 m de largo llega a una pared de D=1 m de diámetro), el efecto local siempre será importante en los tramos más próximos; e.g. el primer tramo de Dx=5 cm (para N=20) emitiría casi la mitad hacia la pared, y a su vez recibiría calor de ésta).
Si no estuviese todo a la sombra, habría que ver la inclinación de la radiación solar incidente, y añadir en cada tramo la energía absorbida. Todavía se complicaría más el problema si hubiera que considerar ganancias por reflexión solar en cuerpos próximos y emisión IR proveniente de ellos.
Con el sol perpendicular al mástil sería:
| > | eqBE:='As*dx*rho*c*dT/dt'=d*dx*alpha*E-(k*As*dT/dx)[x+dx]+(k*As*dT/dx)[x]-Pi*d*dx*epsilon*sigma*(T^4-Ta^4);eqBE:=rho*c*Diff(T,t)=k*Diff(T,x,x)+(d/'As')*(alpha*E-Pi*epsilon*sigma*(T^4-Ta^4)); |
| (14) |
| > | T:='T':N:='N':Fo:='Fo':A:='A':Dt:='Dt':Dx:='Dx':eq0:=subs(epsilon[lat]=epsilon,E0=0,h0=0,h[lat]=0,epsilon0=0,phi=0,eq11_24_0_):eqi:=subs(epsilon[lat]=epsilon,h[lat]=0,phi=0,epsilon0=0,eq11_24_gen_):eqN:=k*A*(T[N+1,j]-T[N,j])/Dx=Wdis-Pi*D^2*epsilon*sigma*(T[N+1]^4-Tinf^4):eq0:=lhs(eq0)=rhs(eq0)+p*alpha*E*Dt/(Pi*rho*c*A);eqi:=lhs(eqi)=rhs(eqi)+p*alpha*E*Dt/(Pi*rho*c*A);eqN:=lhs(eqN)=rhs(eqN)+alpha*(Pi*D^2/4)*E; |
| (15) |
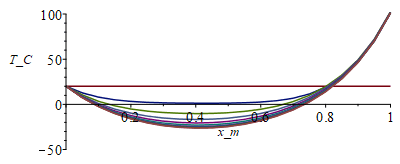
| > | o:=273.15:T:='T':Fo:='Fo':N:=20;Dx:=evalf(subs(dat,SI0,L/N));tsim:=2000;M:=301;Dt:=evalf(tsim/M);eqFo:=Fo=k*'Dt'/(rho*c*Dx^2);Fo:=subs(dat,SI0,rhs(%));p_:=subs(dat,SI0,Pi*d);alpha_:=subs(dat,SI0,alpha);E_:=subs(dat,SI0,E);epsilon_:=subs(dat,SI0,epsilon);sigma_:=subs(dat,SI0,sigma);k_:=subs(dat,SI0,k);rho_:=subs(dat,SI0,rho);c_:=subs(dat,SI0,c);A_:=subs(dat,SI0,As_);delta_:=subs(dat,SI0,delta);d_:=subs(dat,SI0,d);T0_:=subs(dat,SI0,Ta);D_:=subs(dat,SI0,D);Wdis_:=subs(dat,SI0,Wdis);T:=Matrix(1..M,1..N+1,T0_):for j from 1 to M-1 do T[j+1,1]:=T0_;for i from 2 to N do T[j+1,i]:=T[j,i]+Fo*(T[j,i-1]-2*T[j,i]+T[j,i+1])+p_*Dt*(alpha_*E_/Pi-epsilon_*sigma_*(T[j,i]^4-0))/(rho_*c_*A_);od:eq:=subs(SI0,k_*As_*(Tx-T[j+1,N])/Dx)=Wdis_+alpha_*E_*Pi*D_^2/4-Pi*D_^2*epsilon_*sigma_*Tx^4; T[j+1,N+1]:=fsolve(eq,Tx=10..1000);od:i:='i':j:='j':MM:=30:sx:=seq([seq([(i-1)*Dx,T[1+(jm-1)*MM,i]-o],i=1..N+1)],jm=1..(M-1)/MM):plot([sx],x_m=0..1,T_C=-50..100);st:=seq([seq([j*Dt,T[j,i]-o],j=1..M)],i=1..N+1):plot([st],t_s=0..tsim,T_C=-50..103);Tmax_:=TKC(max(T)*K_);Tmin_:=TKC(min(T)*K_);Qt0_:=subs(SI0,-k_*As_*(T[M,2]-T[M,1])/Dx)*W_;QtL_:=subs(SI0,k_*As_*(T[M,N+1]-T[M,N])/Dx)*W_; |
 |
|
 |
|
| (16) |
i.e. con sol se alcanza Tmax=102 ºC y Tmin=-27 ºC (frente a 94 ºC y -50 ºC en sombra), y los flujos de calor que entran por los extremos pasan a ser 1,4 W y 3,5 W (antes, sin sol, eran 2 W y 3,8 W).
Si todas las superficies fuesen cuerpos negros, este último caso con el sol perpendicular al mástil quedaría:
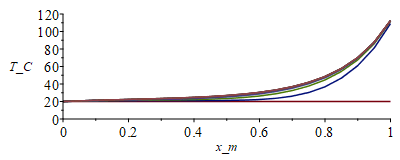
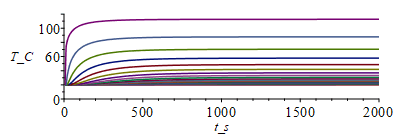
| > | o:=273.15:T:='T':Fo:='Fo':N:=20;Dx:=evalf(subs(dat,SI0,L/N));tsim:=2000;M:=301;Dt:=evalf(tsim/M);eqFo:=Fo=k*'Dt'/(rho*c*Dx^2);Fo:=subs(dat,SI0,rhs(%));p_:=subs(dat,SI0,Pi*d);alpha_:=1+0*subs(dat,SI0,alpha);E_:=subs(dat,SI0,E);epsilon_:=1+0*subs(dat,SI0,epsilon);sigma_:=subs(dat,SI0,sigma);k_:=subs(dat,SI0,k);rho_:=subs(dat,SI0,rho);c_:=subs(dat,SI0,c);A_:=subs(dat,SI0,As_);delta_:=subs(dat,SI0,delta);d_:=subs(dat,SI0,d);T0_:=subs(dat,SI0,Ta);D_:=subs(dat,SI0,D);Wdis_:=subs(dat,SI0,Wdis);T:=Matrix(1..M,1..N+1,T0_):for j from 1 to M-1 do T[j+1,1]:=T0_;for i from 2 to N do T[j+1,i]:=T[j,i]+Fo*(T[j,i-1]-2*T[j,i]+T[j,i+1])+p_*Dt*(alpha_*E_/Pi-epsilon_*sigma_*(T[j,i]^4-0))/(rho_*c_*A_);od:eq:=subs(SI0,k_*As_*(Tx-T[j+1,N])/Dx)=Wdis_+alpha_*E_*Pi*D_^2/4-Pi*D_^2*epsilon_*sigma_*Tx^4; T[j+1,N+1]:=fsolve(eq,Tx=10..1000);od:i:='i':j:='j':MM:=30:sx:=seq([seq([(i-1)*Dx,T[1+(jm-1)*MM,i]-o],i=1..N+1)],jm=1..(M-1)/MM):plot([sx],x_m=0..1,T_C=0..120);st:=seq([seq([j*Dt,T[j,i]-o],j=1..M)],i=1..N+1):plot([st],t_s=0..tsim,T_C=0..120);Tmax_:=TKC(max(T)*K_);Tmin_:=TKC(min(T)*K_);Qt0_:=subs(SI0,-k_*As_*(T[M,2]-T[M,1])/Dx)*W_;QtL_:=subs(SI0,k_*As_*(T[M,N+1]-T[M,N])/Dx)*W_; |
 |
|
 |
|
| (17) |
i.e. todo el mástil quedaría a mayor temperatura que el satélite y en el encastre éste recibiría 0,1 W por el tubo.
Por último, si se hubieran tomado los valores termoópticos del aluminio especular, alpha=0,15 y epsilon=0,05, este caso con sol perpendicular al mástil quedaría:
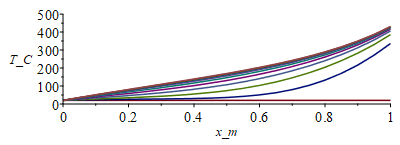
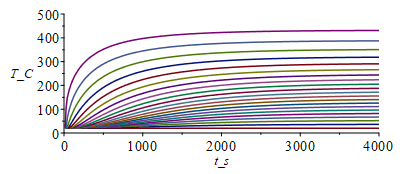
| > | o:=273.15:T:='T':Fo:='Fo':N:=20;Dx:=evalf(subs(dat,SI0,L/N));tsim:=4000;M:=301;Dt:=evalf(tsim/M);eqFo:=Fo=k*'Dt'/(rho*c*Dx^2);Fo:=subs(dat,SI0,rhs(%));p_:=subs(dat,SI0,Pi*d);alpha_:=0.15+0*subs(dat,SI0,alpha);E_:=subs(dat,SI0,E);epsilon_:=0.05+0*subs(dat,SI0,epsilon);sigma_:=subs(dat,SI0,sigma);k_:=subs(dat,SI0,k);rho_:=subs(dat,SI0,rho);c_:=subs(dat,SI0,c);A_:=subs(dat,SI0,As_);delta_:=subs(dat,SI0,delta);d_:=subs(dat,SI0,d);T0_:=subs(dat,SI0,Ta);D_:=subs(dat,SI0,D);Wdis_:=subs(dat,SI0,Wdis);T:=Matrix(1..M,1..N+1,T0_):for j from 1 to M-1 do T[j+1,1]:=T0_;for i from 2 to N do T[j+1,i]:=T[j,i]+Fo*(T[j,i-1]-2*T[j,i]+T[j,i+1])+p_*Dt*(alpha_*E_/Pi-epsilon_*sigma_*(T[j,i]^4-0))/(rho_*c_*A_);od:eq:=subs(SI0,k_*As_*(Tx-T[j+1,N])/Dx)=Wdis_+alpha_*E_*Pi*D_^2/4-Pi*D_^2*epsilon_*sigma_*Tx^4; T[j+1,N+1]:=fsolve(eq,Tx=10..1000);od:i:='i':j:='j':MM:=30:sx:=seq([seq([(i-1)*Dx,T[1+(jm-1)*MM,i]-o],i=1..N+1)],jm=1..(M-1)/MM):plot([sx],x_m=0..1,T_C=0..500);st:=seq([seq([j*Dt,T[j,i]-o],j=1..M)],i=1..N+1):plot([st],t_s=0..tsim,T_C=0..500);Tmax_:=TKC(max(T)*K_);Tmin_:=TKC(min(T)*K_);Qt0_:=subs(SI0,-k_*As_*(T[M,2]-T[M,1])/Dx)*W_;QtL_:=subs(SI0,k_*As_*(T[M,N+1]-T[M,N])/Dx)*W_; |
 |
|
 |
|
| (18) |
i.e. la esfera (si todo fuera de aluminio pulido), alcanzaría 430 ºC, lo que muestra lo malo que es para el control térmico usar acabados especulares de primera superficie, salvo que se quieran para calentar, pues aunque absorben poca energía solar (alpha=0,15), casi no emiten nada (epsilon=0,05), i.e. son captadores solares (por ser alpha/epsilon>>1).
| > |