>	restart:#"m11_p84"

Considérese una tarjeta electrónica (PCB) de 1501001 mm3 compuesta de un recubrimientos de 35 m de cobre para la circuitería, un dieléctrico laminado de 0,5 mm de espesor, y una placa de aluminio 6061-T6 de 0.5 mm de espesor. En el centro de la placa hay un gran circuito integrado (IC) cuadrado, de 60 mm de lado y 2 mm de espesor, que disipa 20 W y no debe superar los 100 ºC, cuya conductividad térmica efectiva es k=50 W/(m·K) en el plano, k=5 W/(m·K) perpendicularmente (puede despreciarse la resistencia térmica de contacto con la placa), y su capacidad térmica es C=10 J/K. Para el resto de componentes de la placa se va a considerar una disipación uniformemente distribuida de 2 W y capacidad térmica despreciable. Se supondrá además que las pistas de cobre solo cubren un 10 % del área en planta de la placa, la cual está empotrada en sus dos lados menores, que se piensa mantener a 20 ºC, mientras que los lados mayores pueden considerarse aislados. Se pide:
a) Estimar la temperatura máxima en la PCB con un modelo unidimensional (1D) de transmisión de calor por conducción considerando toda la disipación concentrada en el punto medio.
b) Estimar el tiempo de relajación térmica, y la dilatación térmica en ausencia de topes.
c) Determinar la conductividad efectiva, y la temperatura máxima de la placa, con un modelo 1D para la disipación distribuida dada.
d) Temperatura máxima considerando que además se transmite calor por radiación, con una emisividad media de 0,9 por el lado de los componentes, y de 0,5 por la cara opuesta, con una caja electrónica que se puede suponer negra y a 45 ºC. ¿Qué influencia tendría añadir el efecto de la convección con aire encerrado, suponiendo un coeficiente de 2 W/(m2·K)?
e) Calcular el calor que llega a los encastres en el caso anterior, y compararlo con el caso conductivo puro.
f) Evolución espacio-temporal de la temperatura si se considera un funcionamiento periódico en el que, durante 60 minutos de cada 90 minutos, el IC consume la mitad de potencia.
g) Resolver el problema térmico bidimensional estacionario.
h) Comprobar si se cumplen los límites aceptables, y proponer cambios que mejoren los márgenes.
Datos del laminado:=2200 kg/m3, c=1000 J/(kg·K)), k=2.5 W/(m·K) en el plano y k=0.5 W/(m·K) perpendicularmente, temperatura máxima de trabajo Tmax=150 ºC.
read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):interface(rtablesize=infinity):

>	dat:=[Lx=0.075*m_,Ly=0.1*m_,Lz=1e-3*m_,Lcu=35e-6*m_,f=0.1,Ldi=0.5e-3*m_,Lal=0.5e-3*m_,Licx=30e-3*m_,Licz=2e-3*m_,Wic=10*W_,Cic=5*J_/K_,Wrest=1*W_,Tb=(20+273.15)*K_,T0=(45+273.15)*K_,epsilon1=0.9,epsilon2=0.5,h12=2*W_/(m_^2*K_)];#Values for half PCB.

Eqs. const. (I=IC, C=Cobre, D=Dielectric, A=Aluminium):

>

datI:=k=50*W_/(m_*K_),kt=5*W_/(m_*K_);datC:=rho=8910*kg_/m_^3,c=390*J_/(kg_*K_),k=400*W_/(m_*K_),CTE=17e-6/K_;datD:=rho=2200*kg_/m_^3,c=1000*J_/(kg_*K_),k=2.5*W_/(m_*K_),kt=0.5*W_/(m_*K_),CTE=20e-6/K_;datA:=rho=2710*kg_/m_^3,c=960*J_/(kg_*K_),k=180*W_/(m_*K_),CTE=23.4e-6/K_;dat:=op(dat),Const,SI2,SI1:

a) Estimar la temperatura máxima en la PCB con un modelo unidimensional (1D) de transmisión de calor por conducción considerando toda la disipación concentrada en el punto medio.

El problema puede considerarse unidimensional porque una dimensión (la z) es muy pequeña (1 frente a 100), y en otra (la y) apenas habrá gradientes (por estar aislada en los extremos y estar la disipación bastante distribuida); así que el calor va a fluir básicamente en dirección x, desde los componentes (fuentes) hacia el borde anclado (sumidero), a través de la PCB (los componentes no llegan al borde). Como el problema es simétrico, consideramos solo una mitad (la izquierda); con el modelo 1D no hay ventaja en coger solo la cuarta parte (doble simetría). El perfil T(x) será recto (solo se considera la fuente en el extremo, i.e. el centro de la PCB), pero como la conductividad térmica efectiva será mayor en la parte del IC, el perfil T(x) constará de dos tramos rectos.

Para calcular la keff en cada tramo tomamos un área de paso constante, A=Ly*Lz=100 mm2. Sea 1 el tramo sin IC, y 2 el tramo bajo el IC.

>

eqF:=Q=-k[eff]*A*dT/dx;eqA:=A=Ly*Lz;eqA_:=subs(dat,%);%*1e6;eqL:=L=Lx;eqL_:=subs(dat,%);eqLi:=Li=Lx-Licx;eqLi_:=subs(dat,%);eqkeff:=k=Sum(k[i]*f[i]*delta[i],i)/Sum(delta[i],i);eqkeff1:=k1=(kcu*f*Lcu+kdi*Ldi+kal*Lal)/Lz;eqkeff1_:=subs(kcu=k,datC,kdi=k,datD,kal=k,datA,eqL,dat,%);eqkeff2:=k2=(kic*Licz+kcu*f*Lcu+kdi*Ldi+kal*Lal)/Lz;eqkeff2_:=subs(kic=k,datI,kcu=k,datC,kdi=k,datD,kal=k,datA,eqL,dat,%);

	(1)

i.e. referido al espesor de 1 mm, en el trama 1 (sin IC) es keff=93 W/(m·K) y en el otro 193 W/(m·K). Como el flujo de calor ha de ser constante (los 11 W que salen hacia la izquierda han de recorrer toda la placa) y la T(x) es continua, se tiene:

>

eqQ:=Q=Wic+Wrest;eqQ_:=subs(dat,%);eqQ1:=Q=k1*A*(Ti-Tb)/Li;eqQ2:=Q=k2*A*(Tm-Ti)/(L-Li);sol_:=subs(dat,solve(subs(eqQ_,eqA_,eqL_,eqLi_,eqkeff1_,eqkeff2_,dat,{eqQ1,eqQ2}),{Ti,Tm}));'Ti'=TKC(subs(sol_,Ti));'Tm'=TKC(subs(sol_,Tm));plot(subs(eqL_,eqLi_,sol_,dat,SI0,piecewise(x<rhs(eqLi_),Tb+(Ti-Tb)*x/Li,Ti+(Tm-Ti)*(x-Li)/(L-Li)))-273,x=0..rhs(eqL_)/m_,T_C=0..100);

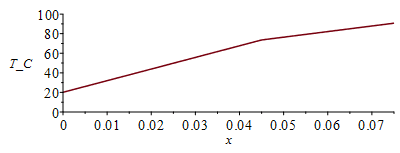i.e. el centro alcanzaría 91 ºC, bastante alta pero aceptable.

Para esta primera aproximación, podría incluso haberse considerado solo la conducción por el aluminio:

>	eqQ0:=Q=k*A*(Tm-Tb)/L;eqk0:=k=kal;eqk0_:=k=subs(datA,k);eqA0:=A=Lal*Ly;eqA0_:=subs(dat,%);%*1e6;Tm_:=subs(eqQ_,eqk0_,eqA0_,eqL,dat,solve(eqQ0,Tm));'Tm_'=TKC(%);

	(2)

i.e. el centro alcanzaría más de 112 ºC, que ya no es aceptable para el IC. Vemos el beneficioso efecto del aumento de la conductividad debido al propio IC.

b) Estimar el tiempo de relajación térmica, y la dilatación térmica en ausencia de topes.

Una primera estimación sería  no incluir las pérdidas y ver el tiempo que se tarda en calentar esa masa hasta esa temperatura. Tomando la temperatura máxima antes calculada, y contando con la capacidad térmica del IC.

>

eqDt_rel_noloss:=Dt=m*c*DT/Q;eqDt_rel_noloss:=Dt=Ct*DT/Q;eqCt:=Ct=Cic+rho*c*V[pcb];eqC:=rho*c=rho_di*c_di+rho_al*c_al;eqC:=rho*c=subs(datD,rho*c)+subs(datA,rho*c);eqV[pcb]:=V[pcb]=subs(dat,Lx*Ly*Lz);eqCt_:=subs(rho=1,c=rhs(eqC),eqV[pcb],dat,eqCt);eqDT:=DT=Tm-Tb;eqDT_:=subs(sol_,dat,%);eqDt_rel_noloss_:=subs(eqCt_,eqDT_,eqQ_,dat,eqDt_rel_noloss);

	(3)

i.e. tardaría unos 260 s en calentarse todo sin pérdidas. Si contamos las pérdidas en la base, el tiempo de relajación dependerá de la difusividad térmica, por lo que habrá que estimarla para cada tramo.

>	eqDt_rel_loss:=Dt=L^2/a;eqDt_rel_loss1:=Dt=rho*c*Li^2/k1;eqDt_rel_loss2:=Dt=(Ct/V[pcb])*(L-Li)^2/k2;eqDt_rel_loss1_:=subs(rho=1,c=rhs(eqC),eqkeff1_,eqLi_,dat,eqDt_rel_loss1);eqDt_rel_loss2_:=subs(eqCt_,eqkeff2_,eqL_,eqLi_,eqV[pcb],dat,eqDt_rel_loss2);

	(4)

i.e. el tiempo de relajación será el mayor, del orden de 100 s (vemos que la parte que está debajo del IC tarda menos en atemperarse porque su mayor conductividad).

En cuanto a la dilatación, tomando la T máxima anterior (sería mejor un valor medio) y el coeficiente de dilatación mayor (CTE, el del aluminio):

>	eqDL:=DL=alpha*DT*L;eqDL:=DL=alpha[al]*(Tm-Tb)*Lx*2;eqDL_:=DL=subs(datA,sol_,dat,CTE*(Tm-Tb)*Lx*2);%*1e3

	(5)

i.e. la PCB se dilataría como máximo 0,25 mm (frente a los 150 mm totales), si no estuviese encastrada.

c) Determinar la conductividad efectiva, y la temperatura máxima de la placa, con un modelo 1D para la disipación distribuida dada.

Ya vimos que, referido al espesor de 1 mm, la keff del conjunto dieléctrico/aluminio es 93 W/(m·K), mientras que en la zona con el IC (pero referido al mismo 1 mm), era keff=193 W/(m·K).

El perfil T(x) estará compuesto de dos tramos parabólicos (con disipación uniforme en cada uno):

>	eqHT:=rho*c*Diff(T,t)=k*Diff(T,x,x)+phi;eqHT:=0=k*diff(T(x),x,x)+phi;sol:=dsolve(%,T(x));eqT1:=T1=Tb+a1*x-phi1*x^2/(2*k1);eqT2:=T2=Ti+a2*(x-Lx+Licx)-phi2*(x-Lx+Licx)^2/(2*k2)

	(6)

Tramo 1:

>

eqQ10:=Q0=k1*A*Diff(T1(x),x)[x=0];eqQ10:=Q0=k1*A*subs(x=0,diff(rhs(eqT1),x));a1_:=subs(Q0=Q,eqQ_,eqkeff1_,eqA_,solve(%,a1));eqTi:=Ti=T1(x)[x=x1];eqTi:=Ti=subs(x=Lx-Licx,rhs(eqT1));eqphi1:=phi1=Wrest/((Lx-Licx)*Ly*Lz);eqphi1_:=subs(dat,%);Ti_:=subs(a1=a1_,eqkeff1_,eqphi1_,dat,rhs(eqTi));'Ti_'=TKC(%);eqT1_:=subs(a1=a1_,eqphi1_,eqkeff1_,dat,SI0,eqT1);

	(7)

Tramo 2:

>

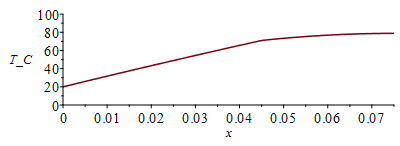
eqQ1i:=Q1=k2*A*diff(T2(x),x)[x=x1];eqQ1i:=Q1=k2*A*subs(x=Lx-Licx,diff(rhs(eqT2),x));eqQ1:=Q1=Wic;eqQ1_:=subs(dat,%);a2_:=subs(eqQ1_,eqkeff2_,eqA_,solve(eqQ1i,a2));eqTm:=Tm=subs(x=Lx,rhs(eqT2));eqphi2:=phi2=Wic/(Licx*Ly*Lz);eqphi2_:=subs(dat,%);Tm_:=subs(Ti=Ti_,a2=a2_,eqkeff2_,eqphi2_,dat,rhs(eqTm));'Tm_'=TKC(%);eqT2_:=subs(Ti=Ti_,a2=a2_,eqphi2_,eqkeff2_,dat,SI0,eqT2);T12_:=piecewise(x<subs(dat,SI0,Lx-Licx),rhs(eqT1_),rhs(eqT2_));plot(T12_-273.15,x=0..subs(dat,SI0,Lx),T_C=0..100);Q12_:=piecewise(x<subs(dat,SI0,Lx-Licx),subs(SI0,rhs(eqkeff1_)*rhs(eqA_)*diff(rhs(eqT1_),x)),subs(SI0,rhs(eqkeff2_)*rhs(eqA_)*diff(rhs(eqT2_),x)));plot(Q12_,x=0..subs(dat,SI0,Lx),Q=-0..12);

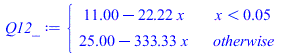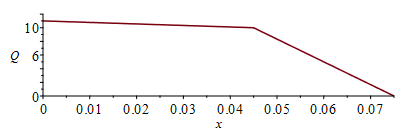i.e. ahora es Tmax=79 ºC en vez de los 91 ºC anteriores. Se ha dibutado T(x) y Q(x) (flujo de calor que va saliendo hacia la izquierda en cada sección x).

Nótese que se ha despreciado siempre la caída de temperatura perpendicularmente al dieléctrico, cuyo valor máximo se puede estimar por transmisión de los 20 W a través del área en planta del IC, Q=k*A*DT/Lzic;

>

i.e. ahora es Tmax=79 ºC en vez de los 91 ºC anteriores. Se ha dibutado T(x) y Q(x) (flujo de calor que va saliendo hacia la izquierda en cada sección x).

Nótese que se ha despreciado siempre la caída de temperatura perpendicularmente al dieléctrico, cuyo valor máximo se puede estimar por transmisión de los 20 W a través del área en planta del IC, Q=k*A*DT/Licz; i.e. DT=Q*Licz/(k*A)=20*0,0005/(0,5*0,06^2)=5,5 K, que no es despreciable, lo que significa que la base del IC estaría 5,5 ºC más caliente que la Tmax calculada por conducción longitudinal, aunque en la realidad, cuando se tenga en cuenta la radiación y la convección, el efecto de la conductancia perpendicular no será tan grande.

d) Temperatura máxima considerando que además se transmite calor por radiación, con una emisividad media de 0,9 por el lado de los componentes, y de 0,5 por la cara opuesta, con una caja electrónica que se puede suponer negra y a 45 ºC. ¿Qué influencia tendría añadir el efecto de la convección con aire encerrado, suponiendo un coeficiente de 2 W/(m2·K)?

Hay que añadir unos sumideros distribuidos para modelar las pérdidas al ambiente, que no serán uniformes porque dependen de la temperatura local. Si sólo se añadiese la convección, el problema seguiría siendo lineal y con solución analítica, pero con la radiación hay que resolverlo numéricamente (o linealizar). Vamos a resolverlo numéricamente, y no solo el estado estacionario sino el transitorio (problema parabólico), que es más sencillo que directamente el estacionario (problema elíptico).

Solución numérica. Sea N el número de tramos (N+1 puntos):

El modelo explícito por diferencias finitas 1D con conductividad no uniforme es:

>	eq11_24;subs(E0=0,h0=0,epsilon0=0,eq11_24_gen);subs(E0=0,h0=0,epsilon0=0,eq11_24_0);subs(EN=0,hN=0,epsilonN=0,eq11_24_N);

	(8)

donde los parámetros rho*c*A, k*A, y phi*A varían con x. Si tomamos un área transversal de referencia fija (A=Lz*Ly), los parámetros variantes son:

>

k:=subs(eqkeff1_,eqkeff2_,eqLi_,dat,SI0,piecewise(x<Li,k1,k2));plot(k,x=0..rhs(eqL_)/m_,'k'=0..200);eqC1:=subs(SI0,eqC);eqC2:=rho*c+Cic/Vic=subs(dat,SI0,rhs(eqC)+Cic/((Lx-Licx)*Ly*Licz));rc:=piecewise(x<rhs(eqLi_)/m_,rhs(eqC1),rhs(eqC2));plot(rc,x=0..rhs(eqL_)/m_,'rc'=0..6e6);phi:=subs(eqLi_,dat,SI0,piecewise(x<Li,rhs(eqphi1_),rhs(eqphi2_)));plot(phi,x=0..rhs(eqL_)/m_,'phi'=0..4e6);

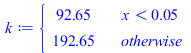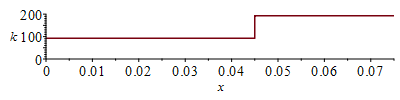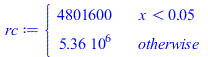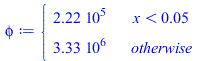Para la discretización tomaremos un tiempo total tsim>trelajación, un N pequeño (para empezar), y un M adecuado para la estabilidad (Fo<1/2).

>

tsim:=750;N:=10;M:=10*N^2;T0_:=subs(dat,SI0,T0);Tb_:=subs(dat,SI0,Tb);Dx:=subs(dat,SI0,Lx)/N;Dt:=evalf(tsim/M);;Lz_:=subs(dat,SI0,Lz);Ly_:=subs(dat,SI0,Ly);Lx_:=subs(dat,SI0,Lx);p:=subs(dat,SI0,2*Ly);sigma:=subs(dat,SI0,sigma);eqFo:=Fo='k*Dt/(rho*c*Dx^2)';eqC1:=subs(SI0,eqC);eqC2:=rho*c+Cic/Vic=subs(dat,SI0,rhs(eqC)+Cic/((Lx-Licx)*Ly*Licz));eqFo1:=Fo1=subs(eqkeff1_,rho=1,c=rhs(eqC1),SI0,k1*Dt/(rho*c*Dx^2));eqFo2:=Fo2=subs(eqkeff2_,rho=1,c=rhs(eqC2),SI0,k2*Dt/(rho*c*Dx^2));

	(9)

Tomaremos un valor inicial de temperatura de la placa igual a la del encastre,T(x)=Tb=20 ºC.

Vamos a comprobar la bondad del códugo numérico resolviendo el caso anterior (solo conducción):

>

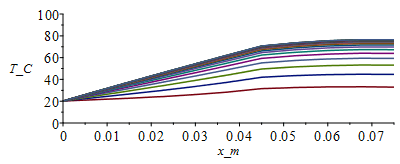
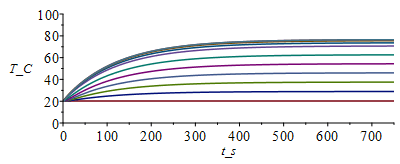
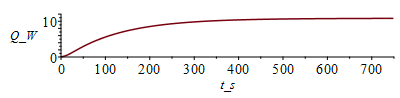
cas0:=h=0,epsilon=0;T:=Matrix(1..M,1..N+1,Tb_):for j from 1 to M-1 do T[j+1,1]:=Tb_;T[j+1,N+1]:=T[j,N]; for i from 2 to N do T[j+1,i]:=T[j,i]+subs(x=(i-1)*Dx+Dx/2,Dt/(rc*Dx^2))*(subs(x=(i-1)*Dx+Dx/2,k)*(T[j,i+1]-T[j,i])-subs(x=(i-1)*Dx-Dx/2,k)*(T[j,i]-T[j,i-1]))+subs(x=(i-1)*Dx,Dt*phi/rc)-subs(cas0,eqA_,SI0,x=(i-1)*Dx,(Dt/(rc*A))*(2*h*Ly_*(T[j,i]-T0_)+2*epsilon*Ly_*sigma*(T[j,i]^4-T0_^4)));od:Q0_[j,1]:=subs(SI0,rhs(eqkeff1_)*rhs(eqA_)*(T[j,2]-T[j,1])/Dx):od:Tmax:=evalf(max(T[M,1..N]))*K_;Tmax:=TKC(%);i:='i':j:='j':sx:=seq([seq([i*Dx-Dx,T[j*50-9,i]-273],i=1..N+1)],j=1..M/50):plot([sx],x_m=0..Lx_,T_C=0..100);st:=seq([seq([j*Dt,T[j,i]-273],j=1..M)],i=1..N+1):plot([st],t_s=0..M*Dt,T_C=0..100);plot([seq([Dt*(j-1),Q0_[j,1]],j=1..M-1)],t_s=0..M*Dt,Q_W=0..12);Q0last:=Q0_[M-1,1]*W_;

	(10)

i.e. salen 10,8 W por el borde, en lugar de los 11 W exactos. Puede valer (puede mejorarse afinando la discretización).

Si ahora añadimos la radiación:

>

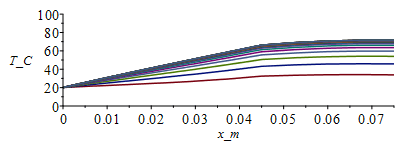
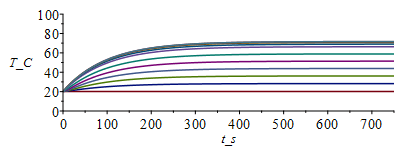
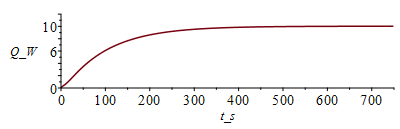
T:='T':cas1:=h=0,epsilon=subs(dat,epsilon1+epsilon2)/2;T:=Matrix(1..M,1..N+1,Tb_):for j from 1 to M-1 do T[j+1,1]:=Tb_;T[j+1,N+1]:=T[j,N]; for i from 2 to N do T[j+1,i]:=T[j,i]+subs(x=(i-1)*Dx+Dx/2,Dt/(rc*Dx^2))*(subs(x=(i-1)*Dx+Dx/2,k)*(T[j,i+1]-T[j,i])-subs(x=(i-1)*Dx-Dx/2,k)*(T[j,i]-T[j,i-1]))+subs(x=(i-1)*Dx,Dt*phi/rc)-subs(cas1,eqA_,SI0,x=(i-1)*Dx,(Dt/(rc*A))*(2*h*Ly_*(T[j,i]-T0_)+2*epsilon*Ly_*sigma*(T[j,i]^4-T0_^4)));od:Q0_[j,1]:=subs(SI0,rhs(eqkeff1_)*rhs(eqA_)*(T[j,2]-T[j,1])/Dx):od:Tmax:=evalf(max(T[M,1..N]))*K_;Tmax:=TKC(%);i:='i':j:='j':sx:=seq([seq([i*Dx-Dx,T[j*50-9,i]-273],i=1..N+1)],j=1..M/50):plot([sx],x_m=0..Lx_,T_C=0..100);st:=seq([seq([j*Dt,T[j,i]-273],j=1..M)],i=1..N+1):plot([st],t_s=0..M*Dt,T_C=0..100);plot([seq([Dt*(j-1),Q0_[j,1]],j=1..M-1)],t_s=0..M*Dt,Q_W=0..12);Q0last:=Q0_[M-1,1]*W_;

	(11)

i.e. con radiación queda Tmax=71,5 ºC y Q0last=10 W, ambos menores que antes.

Nótese que para tiempos cortos el perfil T(x) es convexo debido a la ganancia neta por radiación desde la caja a 45 ºC hacia la placa a 20 ºC.

Si añadimos la convección (y la radiación):

>

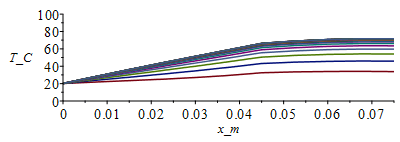
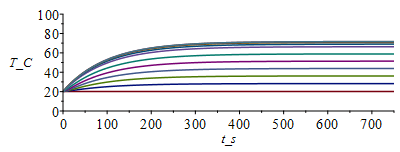
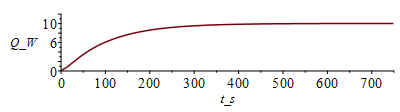
T:='T':cas2:=h=2,epsilon=subs(dat,epsilon1+epsilon2)/2;T:=Matrix(1..M,1..N+1,Tb_):for j from 1 to M-1 do T[j+1,1]:=Tb_;T[j+1,N+1]:=T[j,N]; for i from 2 to N do T[j+1,i]:=T[j,i]+subs(x=(i-1)*Dx+Dx/2,Dt/(rc*Dx^2))*(subs(x=(i-1)*Dx+Dx/2,k)*(T[j,i+1]-T[j,i])-subs(x=(i-1)*Dx-Dx/2,k)*(T[j,i]-T[j,i-1]))+subs(x=(i-1)*Dx,Dt*phi/rc)-subs(cas1,eqA_,SI0,x=(i-1)*Dx,(Dt/(rc*A))*(2*h*Ly_*(T[j,i]-T0_)+2*epsilon*Ly_*sigma*(T[j,i]^4-T0_^4)));od:Q0_[j,1]:=subs(SI0,rhs(eqkeff1_)*rhs(eqA_)*(T[j,2]-T[j,1])/Dx):od:Tmax:=evalf(max(T[M,1..N]))*K_;Tmax:=TKC(%);i:='i':j:='j':sx:=seq([seq([i*Dx-Dx,T[j*50-9,i]-273],i=1..N+1)],j=1..M/50):plot([sx],x_m=0..Lx_,T_C=0..100);st:=seq([seq([j*Dt,T[j,i]-273],j=1..M)],i=1..N+1):plot([st],t_s=0..M*Dt,T_C=0..100);plot([seq([Dt*(j-1),Q0_[j,1]],j=1..M-1)],t_s=0..M*Dt,Q_W=0..12);Q0last:=Q0_[M-1,1]*W_;

	(12)

vemos que apenas hay cambios.

e) Calcular el calor que llega a los encastres en el caso anterior, y compararlo con el caso conductivo puro.

Hemos visto que el calor que sale por el encastre es: si solo hay conducción, 11 W (la mitad del total disipado sale por cada lado), aunque el modelo numérico solo da 10,8 W; si además hay radiación este valor baja a Q0llast=10,0 W; si también hay conveccíón, apenas hay diferencia.

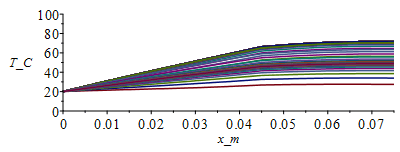
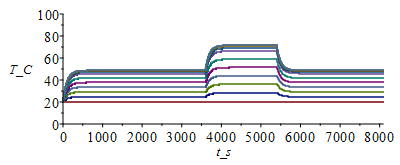
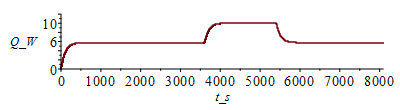
f) Evolución espacio-temporal de la temperatura si se considera un funcionamiento periódico en el que, durante 60 minutos de cada 90 minutos, el IC consume la mitad de potencia.

Como hemos visto que el tiempo de relajación es de unos 5 minutos (300 s) y los cambios son cada 30 min y 60 min, no habrá interferencia entre la respuesta a cada solicitación, pudiendo estudiarse como casos separados. Si representamos un periodo y medio (135 min:

>

T:='T':tsim:=8100;N:=10;M:=110*N^2;T0_:=subs(dat,SI0,T0);Tb_:=subs(dat,SI0,Tb);Dx:=subs(dat,SI0,Lx)/N;Dt:=evalf(tsim/M);;Lz_:=subs(dat,SI0,Lz);Ly_:=subs(dat,SI0,Ly);Lx_:=subs(dat,SI0,Lx);p:=subs(dat,SI0,2*Ly);sigma:=subs(dat,SI0,sigma);eqFo:=Fo='k*Dt/(rho*c*Dx^2)';eqC1:=subs(SI0,eqC);eqC2:=rho*c+Cic/Vic=subs(dat,SI0,rhs(eqC)+Cic/((Lx-Licx)*Ly*Licz));eqFo1:=Fo1=subs(eqkeff1_,rho=1,c=rhs(eqC1),SI0,k1*Dt/(rho*c*Dx^2));eqFo2:=Fo2=subs(eqkeff2_,rho=1,c=rhs(eqC2),SI0,k2*Dt/(rho*c*Dx^2));

	(13)

>

T:='T':cas2:=h=2,epsilon=subs(dat,epsilon1+epsilon2)/2;T:=Matrix(1..M,1..N+1,Tb_):for j from 1 to M-1 do T[j+1,1]:=Tb_;T[j+1,N+1]:=T[j,N]; for i from 2 to N do T[j+1,i]:=T[j,i]+subs(x=(i-1)*Dx+Dx/2,Dt/(rc*Dx^2))*(subs(x=(i-1)*Dx+Dx/2,k)*(T[j,i+1]-T[j,i])-subs(x=(i-1)*Dx-Dx/2,k)*(T[j,i]-T[j,i-1]))+piecewise(j*Dt<3600,0.5,j*Dt>5400,0.5,1)*subs(x=(i-1)*Dx,Dt*phi/rc)-subs(cas1,eqA_,SI0,x=(i-1)*Dx,(Dt/(rc*A))*(2*h*Ly_*(T[j,i]-T0_)+2*epsilon*Ly_*sigma*(T[j,i]^4-T0_^4)));od:Q0_[j,1]:=subs(SI0,rhs(eqkeff1_)*rhs(eqA_)*(T[j,2]-T[j,1])/Dx):od:Tmax:=evalf(max(T[M,1..N]))*K_;Tmax:=TKC(%);i:='i':j:='j':sx:=seq([seq([i*Dx-Dx,T[j*50-9,i]-273],i=1..N+1)],j=1..M/50):plot([sx],x_m=0..Lx_,T_C=0..100);st:=seq([seq([j*Dt,T[j,i]-273],j=1..M)],i=1..N+1):plot([st],t_s=0..M*Dt,T_C=0..100);plot([seq([Dt*(j-1),Q0_[j,1]],j=1..M-1)],t_s=0..M*Dt,Q_W=0..12);Q0last:=Q0_[M-1,1]*W_;

	(14)

i.e. se ve claramente que los transitorios son mucho más cortos que los periodos de trabajo del IC, por lo que estos pueden analizarse independientemente.

g) Resolver el problema térmico bidimensional estacionario.
Se ha resuelto aparte en Matlab, da Tmax=349 K (76 ºC; en el centro del IC), y se comprueba que los gradientes laterales (eje y) son mucho menores que los longitudinales (eje x).

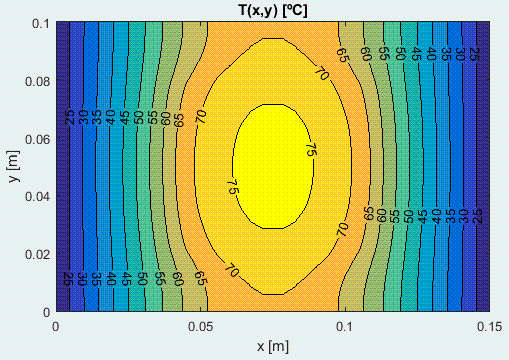
h) Comprobar si se cumplen los límites aceptables, y proponer cambios que mejoren los márgenes.
Está dentro de los límites aceptables incluso teniendo en cuenta el efecto 2D, que eleva 4 ºC la Tmax (desde 72 ºC hasta 76 ºC), y el incremente de temperatura a través del dieléctrico, que será <5,5 ºC como se vio anteriormente.

>