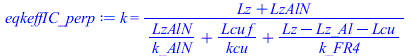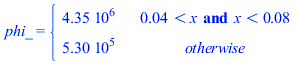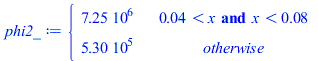p82.mw
Para un anĆ”lisis tĆ©rmico de una tarjeta electrĆ³nica (PCB) se considera el esquema geomĆ©trico de la Fig. 1, donde se representan dos circuitos integrados principales (IC-1 e IC-2). La tarjeta, de 150ļ“115ļ“1,6 mm3, va en una caja a la cual estĆ” empotrada 5 mm por sus dos extremos mĆ”s alejados, las cuales se supondrĆ” que se mantienen siempre a 25 ĀŗC mediante control externo. Las pastillas IC-1 e IC-2, de 37,5ļ“37,5ļ“2,5 mm3, bĆ”sicamente constan de 2 lĆ”minas cerĆ”micas de 1 mm (de nitruro de aluminio, k=150 W/(mĀ·K), ļ²=3200 kg/m3, c=740 J/(kgĀ·K)), y una lĆ”mina interior de 0,5 mm de silicio en cuya parte central de la cara mĆ”s prĆ³xima a la PCB estĆ”n grabadas las uniones electrĆ³nicas (la capa inferior de AlN contiene la matriz de conexiones, lo cual puede ignorarse para este estudio). La PCB se va a suponer constituida por 3 capas: la superior, de 140 ļm de espesor, es la de montaje de los componentes, con pistas de cobre que cubren un 20% del Ć”rea de la PCB; luego una capa intermedia de dielĆ©ctrico (FR-4, k=0,25 W/(mĀ·K), ļ²=1800 kg/m3, c=700 J/(kgĀ·K)), y por Ćŗltimo una capa de aluminio (Al-7075) de 1 mm de espesor. Cada IC disipa 15 W, y se va a considerar que el contacto tĆ©rmico con el zĆ³calo en que va soldado a la PCB es perfecto; el resto de componentes montados sobre la PCB se simularĆ” como una distribuciĆ³n uniforme y constante de 10 W. Se va a establecer un modelo tĆ©rmico unidimensional donde el campo de temperaturas sĆ³lo depende espacialmente de x. Se pide:
a) Determinar el perfil estacionario T(x) suponiendo que la buena conductividad del substrato cerĆ”mico hace que la base de las pastillas (IC-1 e IC-2) puedan considerarse isotermas, y que los 30 W que en ellas se liberan pasan por conducciĆ³n a lo largo de la tarjeta, sin tener en cuenta la disipaciĆ³n en el resto de componentes.
b) Determinar T(x) suponiendo que los 40 W totales se disipasen uniformemente en toda el Ć”rea, y que sĆ³lo se transmite el calor por la PCB.
c) Determinar T(x) con la distribuciĆ³n de disipaciĆ³n dada, ļ(x) [W/m], teniendo en cuenta tambiĆ©n la conducciĆ³n a lo largo de las pastillas principales.
d) AƱadir al modelo conductivo anterior la influencia de la radiaciĆ³n tĆ©rmica desde la capa superior (la de componentes electrĆ³nicos) hasta la caja (que se supondrĆ” tambiĆ©n a 25 ĀŗC); la cara inferior de la PCB estĆ” cerca de otra placa similar y se desprecia el intercambio radiativo. Estudiar tambiĆ©n el efecto del intercambio convectivo con el aire dentro de la caja en el caso lĆmite de temperatura del aire 25 ĀŗC suponiendo un coeficiente convectivo de 5 W/(m2Ā·K).
e) Determinar la temperatura en la zona de uniones electrĆ³nicas de las tarjetas, suponiendo que las temperaturas de los apartados anteriores representan la de la interfaz aluminio/dielĆ©ctrico.
f) Determinar cuĆ”nto tiempo podrĆa hacerse funcionar la tarjeta a partir del momento en que las pastillas IC-1 e IC-2 pasaran de disipar 15 W a 25 W cada una, sabiendo que la temperatura en las uniones electrĆ³nicas no debe superar los 125 ĀŗC (para mejor aproximar la capacidad tĆ©rmica del resto de componentes en este transitorio, considĆ©rese un espesor adicional uniforme de 3 mm de FR-4).
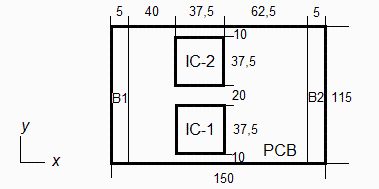
Fig. 1. Esquema de la geometrĆa de la tarjeta (vista en planta por arriba; cotas en mm).
| > |
read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):interface(rtablesize=infinity): |
| > |
su1:="FR4":su2:="Cobre":su3:="Silicio":dat:=[Lx=0.14*m_,Ly=0.115*m_,Lz=1.6e-3*m_,Li1=0.04*m_,Li2=0.0775*m_,LzIC=2.5e-3*m_,LzSi=0.5e-3*m_,k_AlN=150*W_/(m_*K_),rho_AlN=3200*kg_/m_^3,c_AlN=740*J_/(kg_*K_),Lcu=0.14e-3*m_,f=0.2,k_FR4=0.5*W_/(m_*K_),rho_FR4=1800*kg_/m_^3,c_FR4=700*J_/(kg_*K_),Lz_Al=1e-3*m_,Wst_IC=30*W_,Wst_rest=10*W_,Tb=(25+273.15)*K_,Tinf=(25+273.15)*K_,epsilon12=1,h12=5*W_/(m_^2*K_),Wst_IC2=50*W_]; |
Eqs. const. (Cu, Al-7075, Si):
| > |
datCu:=get_sol_data(su2);datSi:=get_sol_data(su3);datAl:=rho=2800*kg_/m_^3,c=960*J_/(kg_*K_),k=120*W_/(m_*K_);dat:=op(dat),Const,SI2,SI1: |
a) Determinar el perfil estacionario T(x) suponiendo que la buena conductividad del substrato cerĆ”mico hace que la base de las pastillas (IC-1 e IC-2) puedan considerarse isotermas, y que los 30 W que en ellas se liberan pasan por conducciĆ³n a lo largo de la tarjeta, sin tener en cuenta la disipaciĆ³n en el resto de componentes.
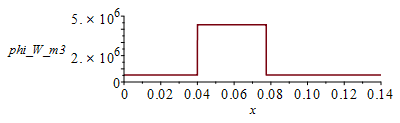
Tenemos una tarjeta con longitud efectiva (no empotrada Lx=140 mm, con una disipaciĆ³n que podemos aproximar como Wst_IC=30 W distribuidos entre 40<x/[mm]<77,5, y el Wst_resto=10 W distribuidos fuera de esa banda. La distribuciĆ³n volumĆ©trica referida a los 1,6 mm de la PCB serĆ”:
| > |
eqphi:=phi=W/(L*Ly*Lz);eqphi_IC:=phi=Wst_IC/((Li2-Li1)*Ly*Lz);eqphi_IC_:=subs(dat,%);eqphi_rest:=phi=Wst_rest/((Lx-Li2+Li1)*Ly*Lz);eqphi_rest_:=subs(dat,%);phi_:=subs(dat,SI0,piecewise(x>Li1 and x<Li2,rhs(eqphi_IC_),rhs(eqphi_rest_)));plot(phi_,x=0..subs(dat,SI0,Lx),phi_W_m3=0..5e6);eqkeff:=k=Sum(k[i]*f[i]*delta[i],i)/Sum(delta[i],i);eqkeff:=k=(kcu*f*Lcu+k_FR4*(Lz-Lz_Al-Lcu)+k_Al*Lz_Al)/Lz;eqkeff_:=k=subs(kcu=k,datCu,k_Al=k,datAl,dat,rhs(%));eqA:=A=Ly*Lz;eqA_:=subs(dat,%); |
Si el tramo disipativo (40<x/[mm]<77,5) es isotermo, y como en los que no hay disipaciĆ³n el perfil T(x) serĆ” recto, basta determinar la Tmax para que el calor que sale por ambos extremos sume Wst_IC.
| > |
eqBE:=k*A*(T1-Tb)/Li1+k*A*(T1-Tb)/(Lx-Li2)=Wst_IC;T1_:=subs(dat,solve(subs(eqkeff_,eqA_,dat,%),T1));'T1_'=TKC(%); |
i.e. la base de los IC alcanzarĆa T1=Tm=73,5 ĀŗC
Si el tramo disipativo (40<x/[mm]<77,5) es isotermo, pero hay disipaciĆ³n fuera, el resto del perfil T(x) serĆ” parabĆ³lico (phi=cte) hasta caer por ambos lados a Tb=25 ĀŗC, y la soluciĆ³n serĆ”:
| > |
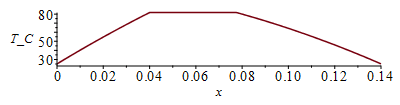
T1:=Tb+b1*x+c1*x^2;T2:=a2+b2*x+c2*x^2;eq12T:=subs(x=Li1,T1)=subs(x=Li2,T2);eqTL:=subs(x=Lx,T2)=Tb;eqQ12:=k*A*(subs(x=Li1,diff(T1,x))-subs(x=Li2,diff(T2,x)))=Wst_IC;eqQ0:=k*A*(subs(x=0,diff(T1,x))-subs(x=Li1,diff(T1,x)))=Wst_rest*Li1/(Lx-Li2+Li1);eqQL:=-k*A*(subs(x=Lx,diff(T2,x))-subs(x=Li2,diff(T2,x)))=Wst_rest*(Lx-Li2)/(Lx-Li2+Li1);sol_:=solve(subs(eqA_,eqkeff_,dat,SI0,{eq12T,eqTL,eqQ12,eqQ0,eqQL}),{b1,c1,a2,b2,c2});T1_:=subs(sol_,dat,SI0,T1);T2_:=subs(sol_,dat,SI0,T2);Tmax_:=subs(x=Li2,dat,SI0,T2_)*K_;'Tmax'=TKC(%);T_:=subs(dat,SI0,piecewise(x<Li1,T1_,x>Li2,T2_,Tmax_));plot(T_-273,x=0..subs(dat,SI0,Lx),T_C=25..Tmax_/K_-273.15); |
i.e. ahora se alcanzarĆan Tm=81,6 ĀŗC.
b) Determinar T(x) suponiendo que los 40 W totales se disipasen uniformemente en toda el Ć”rea, y que sĆ³lo se transmite el calor por la PCB.
El perfil T(x) serƔ una parƔbola simƩtrica, con una Tmax:
| > |
T40:=Tm-a*(x-Lx/2)^2;a_:=solve(Tb=Tm-a*Lx^2/4,a);eqQ0:=k*A*subs(x=0,a=a_,diff(T40,x))=(Wst_IC+Wst_rest)/2;Tm_:=subs(eqkeff_,eqA_,dat,solve(eqQ0,Tm));'Tm_'=TKC(%); |
i.e. con una distribuciĆ³n totalmente uniforme de los 40 W se alcanzarĆa una Tmax=71,4 ĀŗC.
c) Determinar T(x) con la distribuciĆ³n de disipaciĆ³n dada, ļ(x) [W/m], teniendo en cuenta tambiĆ©n la conducciĆ³n a lo largo de las pastillas principales.
Si no tomamos k_IC=infinito sino su valor efectivo, manteniendo el Ɣrea de paso, A=Ly*Lz, tendremos:
| > |
eqkeffIC:=k=Sum(k[i]*f[i]*delta[i],i)/Sum(delta[i],i);eqkeffIC:=k=(k_Si*LzSi+(LzIC-LzSi)*k_AlN+kcu*f*Lcu+k_FR4*(Lz-Lz_Al-Lcu)+k_Al*Lz_Al)/Lz;eqkeffIC_:=k=subs(kcu=k,datCu,k_Al=k,datAl,k_Si=k,datSi,dat,rhs(%)); |
y todavĆa admite soluciĆ³n analĆtica a trozos, ahora con los tres tramos curvos (parabĆ³licos):
| > |
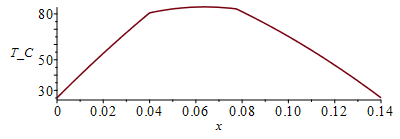
T1:=Tb+b1*x+c1*x^2;T2:=a2+b2*x+c2*x^2;T3:=a3+b3*x+c3*x^2;Q0:=-k0*A*subs(x=0,diff(T1,x));eq1:=subs(x=Li1,T1)=subs(x=Li1,T2);eq1p:=-k0*A*subs(x=Li1,diff(T1,x))=-k1*A*subs(x=Li1,diff(T2,x));Q1:=rhs(%);eq2:=subs(x=Li2,T2)=subs(x=Li2,T3);eq2p:=-k1*A*subs(x=Li2,diff(T2,x))=-k0*A*subs(x=Li2,diff(T3,x));Q2:=rhs(%);QL:=-k0*A*subs(x=Lx,diff(T3,x));eqTL:=subs(x=Lx,T3)=Tb;eqQIC:=-Q1+Q2=Wst_IC;eqQ0:=-Q0+Q1=Wst_rest*Li1/(Lx-Li2+Li1);eqQL:=QL-Q2=Wst_rest*(Lx-Li2)/(Lx-Li2+Li1);sol_:=solve(subs(eqA_,k0=rhs(eqkeff_),k1=rhs(eqkeffIC_),dat,SI0,{eq1,eq1p,eq2,eq2p,eqQIC,eqQ0,eqQL,eqTL}),{a2,a3,b1,b2,b3,c1,c2,c3});Tthree_:=subs(sol_,dat,SI0,piecewise(x<Li1,T1,x>Li2,T3,T2));Tmax:=maximize(Tthree_,x=0..0.14)*K_;'Tmax'=TKC(%);eqCheck:=Qsale=evalf(subs(x=0,k_*A_*diff(Tthree_,x))-subs(x=Lx,dat,SI0,k_*A_*diff(Tthree_,x)));plot(Tthree_-273,x=0..subs(dat,SI0,Lx),T_C=25..Tmax/K_-273.15); |
i.e. la Tmax=84,4 ĀŗC sin radiaciĆ³n ni convecciĆ³n.
d) AƱadir al modelo conductivo anterior la influencia de la radiaciĆ³n tĆ©rmica desde la capa superior (la de componentes electrĆ³nicos) hasta la caja (que se supondrĆ” tambiĆ©n a 25 ĀŗC); la cara inferior de la PCB estĆ” cerca de otra placa similar y se desprecia el intercambio radiativo. Estudiar tambiĆ©n el efecto del intercambio convectivo con el aire dentro de la caja en el caso lĆmite de temperatura del aire 25 ĀŗC suponiendo un coeficiente convectivo de 5 W/(m2Ā·K).
Ya no hay soluciĆ³n analĆtica y hay que resolver numĆ©ricamente. Como hay discontinuidades, hay que detallar los flujos de calor en i-plus y en i-minus (no vale poner la laplaciana).
Primero reslvemos numĆ©ricamente el caso anterior (sin radiaciĆ³n), para estimar la incertidumbre (y para depurar el programa).
| > |
eqHeat:=rho*c*A*dx*dT/dt=(k*A*Tp)[p]-(k*A*Tp)[m]+phi*A*dx-p*dx*h*(T-Tinf);eqHeat:=Tdot=(k[p]*A[p]*Tp[p]-k[m]*A[m]*Tp[m])/(rho*c*A*dx)+phi/(rho*c)-(p/(rho*c*A))*h*(T-Tinf);eqHeati:=T[j+1,i]=T[j,i]+(Dt/(rho*c*A*Dx^2))*(kp*Ap*(T[j,i+1]-T[j,i])-km*Am*(T[j,i]-T[j,i-1]))+Dt*phi/(rho*c)-(Dt*p/(rho*c*A))*(h*(T[j,i]-Tinf)+epsilon*sigma*(T[j,i]^4-Tinf^4));p=0; |
| > |
N:=14;M:=1000;tsim:=500;Tb_:=subs(dat,SI0,Tb);Tinf_:=subs(dat,SI0,Tinf);Tn:=Matrix(1..M,1..N+1,Tb_):Dx:=subs(dat,SI0,Lx/N);Dt:=evalf(tsim/M);eqDt_rceff:='Dt'/(rho*c)='Dt'*Lz/(rho_Cu*c_Cu*f*Lcu+rho_FR4*c_FR4*(Lz-Lz_Al-Lcu)+rho_Al*c_Al*Lz_Al);eqDt_rceff_:='Dt'/(rho*c)=subs(rho_Cu=rho,c_Cu=c,datCu,rho_Al=rho,c_Al=c,datAl,dat,SI0,rhs(%));eqDt_rceffIC:='Dt'/(rho*c)=Dt*Lz/(rho_Si*c_Si*LzSi+(LzIC-LzSi)*rho_AlN*c_AlN+rho_Cu*c_Cu*f*Lcu+rho_FR4*c_FR4*(Lz-Lz_Al-Lcu)+rho_Al*c_Al*Lz_Al);eqDt_rceffIC_:='Dt'/(rho*c)=subs(rho_Si=rho,c_Si=c,datSi,rho_Cu=rho,c_Cu=c,datCu,rho_Al=rho,c_Al=c,datAl,dat,SI0,rhs(%));Dt_rc:=subs(dat,SI0,piecewise(x<Li1,rhs(eqDt_rceff_),x>Li2,rhs(eqDt_rceff_),rhs(eqDt_rceffIC_)));A_:=subs(dat,SI0,Ly*Lz);k_:=subs(dat,SI0,piecewise(x<Li1,rhs(eqkeff_),x>Li2,rhs(eqkeff_),rhs(eqkeffIC_)));Fo_:=subs(dat,k_*Dt_rc/Dx^2):'Fo_'=maximize(Fo_); |
| > |
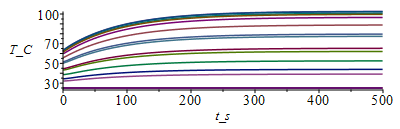
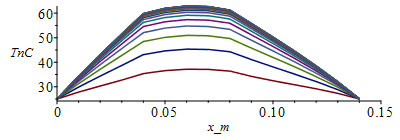
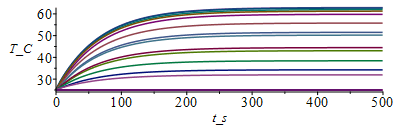
for j from 1 to M-1 do Tn[j+1,1]:=Tb_;Tn[j+1,N+1]:=Tb_; for i from 2 to N do Tn[j+1,i]:=Tn[j,i]+subs(x=(i-1)*Dx+Dx/2,Dt_rc/Dx^2)*(subs(x=(i-1)*Dx+Dx/2,k_)*(Tn[j,i+1]-Tn[j,i])-subs(x=(i-1)*Dx-Dx/2,k_)*(Tn[j,i]-Tn[j,i-1]))+subs(x=(i-1)*Dx+Dx/2,Dt_rc)*subs(x=i*Dx-Dx,phi_);od:od:Tmax:=evalf(max(Tn[M,1..N]))*K_;'Tmax'=TKC(%);Tmax_:=Tmax/K_-273.15:Dm:=50:sx:=seq([seq([i*Dx-Dx,Tn[j*Dm,i]-273.15],i=1..N+1)],j=1..M/Dm):plot([sx],x_m=0..0.15,TnC=25..Tmax_);st:=seq([seq([j*Dt-Dt,Tn[j,i]-273.15],j=1..M)],i=1..N+1):plot([st],t_s=0..tsim,T_C=25..Tmax_); |
i.e. Tmax=75,3 ĀŗC frente a 84,4 ĀŗC; pero con N=28 ya da Tmax=81 ĀŗC. Para comprobar conviene hacer un balance energĆ©tico global y determinar el calor que sale por los extremos (no hay pĆ©rdidas laterales). BastarĆa hacerlo para t=tsim, pero es interesante ver cĆ³mo varĆa con t.
| > |
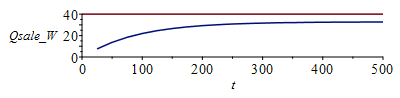
Qsale:=seq([Dt*jm*Dm,evalf(subs(x=i*Dx-Dx,i=2,k_)*A_*(Tn[jm*Dm,2+1]-Tn[jm*Dm,2-1])/(2*Dx))-evalf(subs(x=i*Dx-Dx,i=N,k_)*A_*(Tn[jm*Dm,N+1]-Tn[jm*Dm,N-1])/(2*Dx))],jm=1..M/Dm):plot({subs(dat,SI0,Wst_IC+Wst_rest),[Qsale]},t=0..tsim,Qsale_W=0..40); |
Ahora sĆ aƱadimos la radiaciĆ³n.
| > |
p=2*Ly;p_:=subs(dat,SI0,2*Ly);epsilon=subs(dat,epsilon12);h=subs(dat,h12);for j from 1 to M-1 do Tn[j+1,1]:=Tb_;Tn[j+1,N+1]:=Tb_; for i from 2 to N do Tn[j+1,i]:=Tn[j,i]+subs(x=(i-1)*Dx+Dx/2,Dt_rc/Dx^2)*(subs(x=(i-1)*Dx+Dx/2,k_)*(Tn[j,i+1]-Tn[j,i])-subs(x=(i-1)*Dx-Dx/2,k_)*(Tn[j,i]-Tn[j,i-1]))+subs(x=(i-1)*Dx+Dx/2,Dt_rc)*subs(x=i*Dx-Dx,phi_)-subs(x=(i-1)*Dx+Dx/2,dat,SI0,Dt_rc*(p_/A_)*(h12*(Tn[j,i]-Tinf)+epsilon12*sigma*(Tn[j,i]^4-Tinf^4)));od:od:Tmax:=evalf(max(Tn[M,1..N]))*K_;'Tmax'=TKC(%);Tmax_:=Tmax/K_-273.15:Dm:=50:sx:=seq([seq([i*Dx-Dx,Tn[j*Dm,i]-273.15],i=1..N+1)],j=1..M/Dm):plot([sx],x_m=0..0.15,TnC=25..Tmax_);st:=seq([seq([j*Dt-Dt,Tn[j,i]-273.15],j=1..M)],i=1..N+1):plot([st],t_s=0..tsim,T_C=25..Tmax_); |
i.e. con las pĆ©rdidas radiativas la Tmax baja a 63 ĀŗC frente a los 75 ĀŗC sin pĆ©rdidas.
e) Determinar la temperatura en la zona de uniones electrĆ³nicas de las tarjetas, suponiendo que las temperaturas de los apartados anteriores representan la de la interfaz aluminio/dielĆ©ctrico.
Se trata de un problema unidimensional perpendicular al plano de la tarjeta.
| > |
i:='i';eqkeffIC_perp:=k=Sum(delta[i],i)/Sum(delta[i]/(k[i]*f[i]),i);LzAlN:=(LzIC-LzSi)/2;eqkeffIC_perp:=k='(Lz+LzAlN)/(LzAlN/k_AlN+Lcu/kcu*f+(Lz-Lz_Al-Lcu)/k_FR4)';eqkeffIC_perp_:=k=subs(kcu=k,datCu,dat,rhs(%));eqQIC:=Wst_IC=k*A*(Tjunc-TAl)/'(Lz+LzAlN)';eqAIC:=A=Ly*(Li2-Li1);eqAIC_:=subs(dat,%);TAl='Tn[M,N/3]';TAl_:=evalf(Tn[M-1,floor(N/3)])*K_;'TAl'=TKC(%);Tjunc:=subs(eqAIC_,eqkeffIC_perp_,dat,SI0,TAl_+Wst_IC*(Lz+LzAlN)/(k*A))*K_;'Tjunc'=TKC(%); |
i.e. las uniones bipolares estarĆa a unos 58 ĀŗC, unos 6,5 ĀŗC mĆ”s calientes que la base de aluminio.
f) Determinar cuĆ”nto tiempo podrĆa hacerse funcionar la tarjeta a partir del momento en que las pastillas IC-1 e IC-2 pasaran de disipar 15 W a 25 W cada una, sabiendo que la temperatura en las uniones electrĆ³nicas no debe superar los 125 ĀŗC (para mejor aproximar la capacidad tĆ©rmica del resto de componentes en este transitorio, considĆ©rese un espesor adicional uniforme de 3 mm de FR-4).
Se trata ahora de empezar una nueva simulaciĆ³n, pero empezando con el perfil estacionario antes obtenido para Wst_IC=30 W, que incluye las pĆ©rdicas laterales por radiaciĆ³n, cambiendo ahora la phiIC=4,35 MW/m3 a phiIC2=4,35*50/30=7,25 MW/m3.
| > |
'phi_'=phi_;phi2_:=subs(dat,SI0,piecewise(x>Li1 and x<Li2,rhs(eqphi_IC_)*Wst_IC2/Wst_IC,rhs(eqphi_rest_)));for i from 2 to N do Tn[1,i]:=Tn[M,i];od:Tini:=Tn[1,1..N+1]; |
| > |
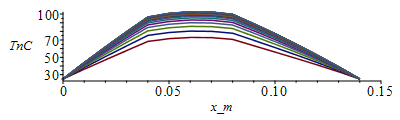
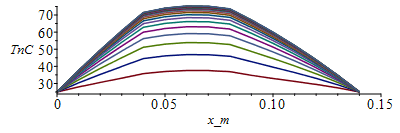
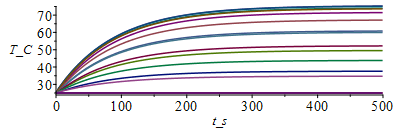
for j from 1 to M-1 do Tn[j+1,1]:=Tb_;Tn[j+1,N+1]:=Tb_; for i from 2 to N do Tn[j+1,i]:=Tn[j,i]+subs(x=(i-1)*Dx+Dx/2,Dt_rc/Dx^2)*(subs(x=(i-1)*Dx+Dx/2,k_)*(Tn[j,i+1]-Tn[j,i])-subs(x=(i-1)*Dx-Dx/2,k_)*(Tn[j,i]-Tn[j,i-1]))+subs(x=(i-1)*Dx+Dx/2,Dt_rc)*subs(x=i*Dx-Dx,phi2_);od:od:Tmax:=evalf(max(Tn[M,1..N]))*K_;'Tmax'=TKC(%);Tmax_:=Tmax/K_-273.15:Dm:=50:sx:=seq([seq([i*Dx-Dx,Tn[j*Dm,i]-273.15],i=1..N+1)],j=1..M/Dm):plot([sx],x_m=0..0.15,TnC=25..Tmax_);st:=seq([seq([j*Dt-Dt,Tn[j,i]-273.15],j=1..M)],i=1..N+1):plot([st],t_s=0..tsim,T_C=25..Tmax_); |
i.e. ahora la base de aluminio alcanza 103 ĀŗC, que mĆ”s los 6,5 ĀŗC de incremento transversal a travĆ©s del FR$ y el AlN, apenas llega a los 110 ĀŗC en las uniones bipolares de los IC, luego no hay lĆmite.


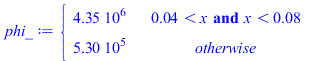
![k = `/`(`*`(Sum(`*`(k[i], `*`(f[i], `*`(delta[i]))), i)), `*`(Sum(delta[i], i)))](images/p821_15.gif)
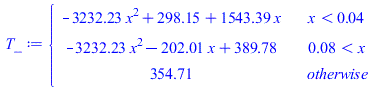
![k = `/`(`*`(Sum(`*`(k[i], `*`(f[i], `*`(delta[i]))), i)), `*`(Sum(delta[i], i)))](images/p821_42.gif)
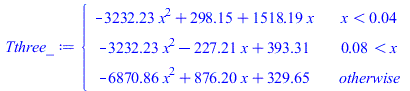
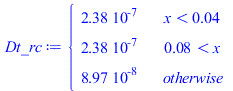

![k = `/`(`*`(Sum(delta[i], i)), `*`(Sum(`/`(`*`(delta[i]), `*`(k[i], `*`(f[i]))), i)))](images/p821_99.gif)