>	restart:#"m11_p80"

Considérese una tarjeta electrónica (PCB) de 1501001,5 mm3 de FR-4*, con un recubrimiento de 50 m de cobre por un lado, y con diversos componentes electrónicos por el otro, que en funcionamiento pueden asimilarse térmicamente a una distribución uniforme de 10 W de disipación total. Sabiendo que la tarjeta se inserta en una placa base por uno de los bordes largos que se mantiene permanentemente a 25 ºC con una refrigeración exterior, se pide:

a) Considerando que la tarjeta sólo evacua calor a través de la conexión, determinar la temperatura máxima que se alcanzaría, con y sin tener en cuenta el recubrimiento de cobre.

b) Considerando que además se transmite calor por convección al aire ambiente, que se va a suponer que está a 40 ºC, con un coeficiente convectivo de 5 W/(m2•K), y por radiación a las paredes (también a 40 ºC), determinar la temperatura máxima suponiendo una emisividad media de 0,7 para ambos lados.

c) Considerando que durante 10 minutos de cada 90 minutos, la tarjeta consume el doble de potencia, determinar la temperatura máxima suponiendo que para el estudio del transitorio, la capacidad térmica de los componentes se pueden asimilar a un espesor uniforme de 5 mm de material adicional a la resina (con las mismas propiedades del FR-4).

*FR-4 es un material compuesto, de fibra de vidrio laminada con resina epoxi (un adhesivo termoestable estructural aislante eléctrico):=1850 kg/m3, c=700 J/(kg•K)), k=0.25 W/(m•K), temperatura máxima de trabajo 140 ºC.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):interface(rtablesize=infinity):

>	su1:="FR4":su2:="Cobre":su3:="Aire":dat:=[Lx=0.1*m_,Ly=0.15*m_,Lz=1.5e-3*m_,Lcu=50e-6*m_,Wst=10*W_,Wunst_Wst=2,Tb=(25+273.15)*K_,T0=(40+273.15)*K_,h=5*W_/(m_^2*K_),epsilon=0.7,Dt_on=600*s_,Lele=0.005*m_];

Eqs. const.:

>	datF:=rho=1850*kg_/m_^3,c=700*J_/(kg_*K_),k=0.25*W_/(m_*K_);datC:=get_sol_data(su2);datA:=get_gas_data(su3):dat:=op(dat),Const,SI2,SI1:

a) Considerando que la tarjeta sólo evacua calor a través de la conexión, determinar la temperatura máxima que se alcanzaría, con y sin tener en cuenta el recubrimiento de cobre.

Problema estacionario de conducción de calor unidimensional plana, con fuentes distribuidas uniformemente (10 W en toda la placa). origen en la base de encastre.

>

eqBElocal:=rho*Ly*Lz*dx*c*diff(T(x,t),t)=Wst*dx/Lx+k*Ly*Lz*dx*diff(T(x,t),x,x);eqBElocal_:=0=phi+k*diff(T(x),x,x);eqT:=T=A*x+B-(phi/(2*k))*x^2;eqphi0:=phi=Wst/(Lx*Ly*Lz);eqBC0:=Tb=B;eqBC1:=Tmax=subs(x=Lx,rhs(eqT));eqB0p:=k*Ly*Lz*dT/dx[x=0]=Wst;eqB0p:=k*Ly*Lz*A=Wst;eqT_:=T=Tb+x*Wst/(k*Ly*Lz)-x^2*Wst/(2*k*Lx*Ly*Lz);k=subs(datF,k);Tmax_:=subs(x=Lx,datF,dat,rhs(eqT_));keff:=(kF*LF+kC*LC)/(LF+LC);keff_:=subs(kF=k,datF,LF=Lz,LC=Lcu,kC=k,datC,dat,keff);Tmax_:=subs(x=Lx,k=keff_,dat,rhs(eqT_));Tmax:=TKC(%);plot(subs(k=keff_,dat,SI0,rhs(eqT_)-273),x=0..subs(dat,SI0,Lx),T_C=0..200);

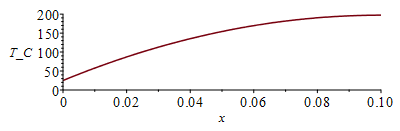i.e. sin le cobre se quemaría la resina (Tmax=9200 K no indica más que eso), y con el cobre el extremo opuesto alcanzaría 197 ºC, insoportable para la resina (se deformaría mucho, o se chumascaría como antes).

b) Considerando que además se transmite calor por convección al aire ambiente, que se va a suponer que está a 40 ºC, con un coeficiente convectivo de 5 W/(m2•K), y por radiación a las paredes (también a 40 ºC), determinar la temperatura máxima suponiendo una emisividad media de 0,7 para ambos lados.

Hay que añadir unos sumideros distribuidos para modelar las pérdidas al ambiente, que no serán uniformes porque dependen de la temperatura local.

Despreciamos las pérdidas de calor longitudinales en el extremo libre de la placa.

Si no se considerara la radiación el problema sería lineal y resoluble analíticamente.

>

eqBElocal:=rho*Ly*Lz*dx*c*diff(T(x,t),t)=Wst*dx/Lx+k*Ly*Lz*dx*diff(T(x,t),x,x)-2*h*Ly*dx*(T(x,t)-T0)-2*epsilon*Ly*dx*sigma*(T(x,t)^4-T0^4);eqBElocal_:=0=phi+k*diff(T(x),x,x)-(2*h/Lz)*(T(x)-T0)-(2*epsilon/Lz)*sigma*(T(x)^4-T0^4);eqT:=dsolve(subs(epsilon=0,{eqBElocal_,T(0)=Tb,D(T)(Lx)=0}),T(x));Tmax_:=evalf(subs(x=Lx,k=keff_,eqphi0,dat,SI0,rhs(eqT)))*K_;Tmax:=TKC(%);plot(subs(k=keff_,eqphi0,dat,SI0,rhs(eqT)-273),x=0..subs(dat,SI0,Lx),T_C=0..100);

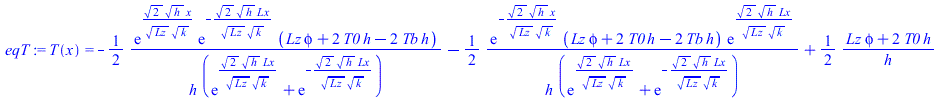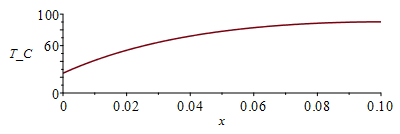i.e. el extremo alcanzaría 90 ºC. Con radiación hay que resolverlo numéricamente. Resolveremos el transitorio (problema parabólico), que es mejor que directamente el estacionario (problema elíptico).

Vamos a poner ya una capacidad térmica equivalente que tenga en cuenta la masa de los componentes electrónicos, dejando las demas dimensiones anteriores, aunque para el régimen estacionario da igual.

Suponemos que los componentes no contribuyen a la conducción de calor en la dirección paralela a la tarjeta.

Tomaremos un valor inicial de temperatura de la placa igual al de la caja (y el aire, T0), pese a que instantáneamente obligamos a que la base cambie de T0=40 ºC a Tb=25 ºC. También se podía haber tomado como inicial el estacionario con W=0 (placa no activada).

>	eq11_24_0_;eq11_24_gen_;eq11_24_N_:T:='T':eq0:=subs(epsilon[lat]=epsilon,E0=0,h0=0,h[lat]=h,epsilon0=0,eq11_24_0_);eqi:=subs(epsilon[lat]=epsilon,h[lat]=h,epsilon0=0,eq11_24_gen_);eqN:=T[N,j+1]=T[N-1,j+1];#eqN:=subs(epsilon[lat]=epsilon,EN=0,hN=0,h[lat]=h,epsilonN=0,eq11_24_N_);

	(1)

>

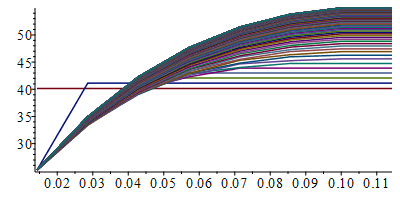
N:=7;M:=150;T0:=subs(dat,SI0,T0);Tb:=subs(dat,SI0,Tb);Dx:=subs(dat,SI0,Lx)/N;Dt:=10;phi:=subs(dat,SI0,rhs(eqphi0));eqrho_eff:=rho[eff]=(rho1*delta1+rho2*delta2)/(delta1+delta2);rho:=subs(rho1=rho,datF,rho2=rho,datC,delta1=Lz,delta2=Lcu,dat,SI0,rhs(%));eqc_eff:=c[eff]=(rho1*delta1*c1+rho2*delta2*c2)/(rho1*delta1+rho2*delta2);c:=subs(c1=c,rho1=rho,datF,c2=c,rho2=rho,datC,delta1=Lz,delta2=Lcu,dat,SI0,rhs(%));Lz:=subs(dat,SI0,Lz);h:=subs(dat,SI0,h);sigma:=subs(dat,SI0,sigma);epsilon:=subs(dat,epsilon);eqFo:=Fo='k*Dt/(rho*c*Dx^2)';Fo:=subs(k=keff_,dat,SI0,rhs(eqFo));Dton:=subs(dat,SI0,Dt_on);Wunst_Wst_:=subs(dat,Wunst_Wst);eq_c_equiv:='cequiv=ceff*Lele/Lz';c:=subs(dat,SI0,c*Lele/Lz);T:=Matrix(1..M,1..N+1,T0):for j from 1 to M-1 do T[j+1,1]:=Tb;for i from 2 to N do T[j+1,i]:=T[j,i]+Fo*(T[j,i-1]-2*T[j,i]+T[j,i+1])+phi*Dt/(rho*c)-(2*Dt/(rho*c*Lz))*(h*(T[j,i]-T0)+epsilon*sigma*(T[j,i]^4-T0^4));od: T[j+1,N+1]:=T[j+1,N];od:Tmax:=max(T)*K_;Tmax:=TKC(%);i:='i':j:='j':sx:=seq([seq([i*Dx,T[j,i]-273],i=1..N+1)],j=1..M):plot([sx]);st:=seq([seq([j*Dt,T[j,i]-273],j=1..M)],i=1..N+1):plot([st]);

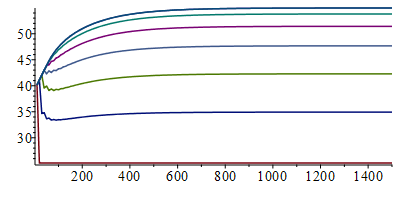i.e., el extremo sólo llega a 55 ºC contabilizanto la radiación (conviene comprobar que si se pone epsilon=0 se recupera el resultado anterior).

c) Considerando que durante 1 minuto de cada 90 minutos, la tarjeta consume el doble de potencia, determinar la temperatura máxima suponiendo que para el estudio del transitorio los componentes se pueden asimilar a un espesor uniforme de 5 mm de material con las propiedades del FR-4.

Como se ha visto que a partir de 1000 s ya se ha alcanzado el régimen, vamos a poner que a los 1500 s tiene lugar el sobrecalentamiento de 60 s de duración.

>

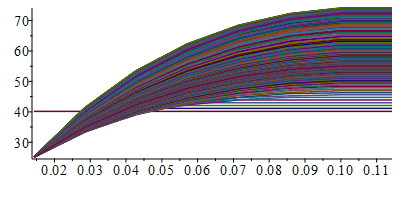
N:=7;M:=300;ph:=Matrix(1..M,1..N+1,phi):Mon:=150;Moff:=Mon+Dton/Dt;for j from Mon to Moff do for i from 1 to N+1 do ph[j,i]:=ph[j,i]*Wunst_Wst_;od:od:ph:T:=Matrix(1..M,1..N+1,T0):for j from 1 to M-1 do T[j+1,1]:=Tb;for i from 2 to N do T[j+1,i]:=T[j,i]+Fo*(T[j,i-1]-2*T[j,i]+T[j,i+1])+ph[j,i]*Dt/(rho*c)-(2*Dt/(rho*c*Lz))*(h*(T[j,i]-T0)+epsilon*sigma*(T[j,i]^4-T0^4));od: T[j+1,N+1]:=T[j+1,N];od:Tmax:=max(T)*K_;Tmax:=TKC(%);i:='i':j:='j':sx:=seq([seq([i*Dx,T[j,i]-273],i=1..N+1)],j=1..M):plot([sx]);st:=seq([seq([j*Dt,T[j,i]-273],j=1..M)],i=1..N+1):plot([st]);

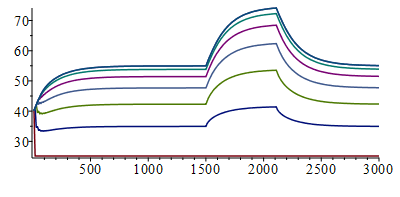Vemos que el transitorio casi llega a desarrollarse del todo en los 10 min de duración (ya habíamos visto que el tiempo de relajación era de unos 1000 s (15 min), alcanzándose en el extremo 74 ºC, que puede que ya sea demasiado para los componentes allí situados..

>