>	restart:#"m11_73"

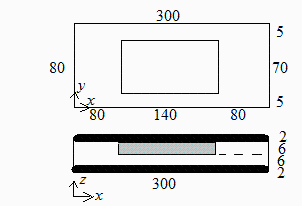
En un satélite se piensa usar una bandeja porta-instrumentos construida en panal, la cual está formada por dos capas de CFRP de 2 mm de espesor, y una capa de espuma sólida (F) de 12 mm de espesor en cuyo interior van alojados los elementos de la batería eléctrica. Se va a estudiar el comportamiento térmico de uno de los módulos laterales de la bandeja, de dimensiones 300×80×16 mm3. En una de las caras de F hay una hendidura centrada que aloja un elemento de batería (B) de Li-ion, de 140×70×6 mm3; el efecto de las conexiones y circuitos auxiliares de la batería no se tienen en cuenta. Se va a estudiar el siguiente modelo térmico simplificado (las propiedades de los materiales se dan en la Tabla 1): el elemento de batería, en el caso más crítico, disipa 1 W durante 30 minutos y está inactivo los siguientes 60 minutos del ciclo. Solo se va a considerar la transmisión de calor por conducción a uno de los extremos cortos del módulo, que se supondrá que permanece a 300 K (los otros tres lados se pueden suponer de simetría). En particular, se pide:

a) Resolver el problema de conducción estacionaria (1 W) desde el elemento de batería (B, que se considerará isotermo en este apartado), hasta el borde de la placa (a Tb=300 K), a través de los dos caminos paralelos: 1) el directo, a lo largo de la cara en contacto; y 2) el indirecto, a través de los 6 mm de espuma y luego a lo largo de la otra lámina de CFRP.

b) Calcular la carga térmica admisible de los equipos que fueran montados sobre la bandeja, para que la temperatura de esta no supere los 75 ºC.

c) Resolver analíticamente el problema de conducción unidimensional estacionaria a lo largo de la capa de CFRP (sin contar la batería), con los 1 W distribuidos uniformemente sobre toda la cara del módulo.

d) Resolver analíticamente el problema de conducción unidimensional estacionaria a lo largo de la capa de CFRP (sin contar la batería), pero ahora con la disipación de energía distribuida uniformemente sólo en la dirección transversal del módulo (los 80 mm).

e) Resolver analíticamente el problema de conducción unidimensional estacionaria a lo largo de la capa de CFRP contabilizando también la conducción en la batería (pero no a través de la espuma).

f) Resolver numéricamente el problema de conducción unidimensional no estacionaria con la variación temporal de la disipación de energía dada.

g) Resolver numéricamente el problema de conducción bidimensional transitorio desde el estado isotermo hasta el estacionario.

Tabla 1. Propiedades de los materiales.

 [kg/m3] c [J/(kg•K)] k [W/(m•K)]

CFRP 1500 840 30 (paralel.)

1,25 (perpend.)

F 75 1200 0.03

B 2400 900 35 (paralel.)

1,5 (perpend)

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):with(plots):interface(rtablesize=infinity):

>

su1:="CFRP":su2:="Foam":su3:="Battery":dat:=[Lx=0.3*m_,Ly=0.08*m_,Lz=0.016*m_,LzC=2e-3*m_,LzF=12e-3*m_,LxB=0.14*m_,LyB=0.07*m_,LzB=0.006*m_,W=1*W_,tW=30*60*s_,tnW=60*60*s_,Tb=300*K_,Tm=(75+273.15)*K_,T0=300*K_,rhoC=1500*kg_/m_^3,cC=840*J_/(kg_*K_),kpC=30*W_/(m_*K_),ktC=1.25*W_/(m_*K_),rhoF=75*kg_/m_^3,cF=1200*J_/(kg_*K_),kF=0.03*W_/(m_*K_),rhoB=2400*kg_/m_^3,cB=900*J_/(kg_*K_),kpB=35*W_/(m_*K_),ktB=1.5*W_/(m_*K_)];

Eqs. const.:

>	datC:=rho=1500*kg_/m_^3,c=840*J_/(kg_*K_),kp=30*W_/(m_*K_),kt=1.25*W_/(m_*K_);datF:=rho=75*kg_/m_^3,c=1200*J_/(kg_*K_),k=0.03*W_/(m_*K_);datB:=rho=2400*kg_/m_^3,c=900*J_/(kg_*K_),kp=35*W_/(m_*K_),kt=1.5*W_/(m_*K_);dat:=op(dat),Const,SI2,SI1:

a) Resolver el problema de conducción estacionaria (1 W) desde el elemento de batería (B, que se considerará isotermo en este apartado), hasta el borde de la placa (a Tb=300 K), a través de los dos caminos paralelos: 1) el directo, a lo largo de la cara en contacto; y 2) el indirecto, a través de los 6 mm de espuma y luego a lo largo de la otra lámina de CFRP.

>

eq0:=Q=DT/R;eq0:=W=(TB-Tb)/R;eqR:=R=L/(k*A);eqR12:=1/R=1/R1+1/R2;X1:=(Lx-LxB)/2;X1_:=subs(dat,%);eqR1:=R1='X1'/(kpC*Ly*LzC);eqR2:=R2=(LzF-LzB)/(kF*Ly*LxB)+'X1'/(kpC*Ly*LzC);eqR1_:=subs(dat,eqR1);eqR2_:=subs(dat,eqR2);eqR12_:=R12=subs(eqR1_,eqR2_,dat,solve(eqR12,R));eq0_:=TB=Tb+W*R12;eq0__:=subs(eqR12_,dat,%);Q1:=DT/R1;Q1_:=subs(eqR1_,eq0__,dat,(TB-Tb)/R1);Q2_:=subs(dat,W)-Q1_;

	(1)

i.e.  la batería (y el trozo de CFRP en contacto directo con ella) queda a TB=311 K, y del 1 W disipado 2/3 (0,67 W) fluyen por la cara en contacto, y 1/3 (0,33 W) por la otra.

b) Estimar la carga térmica admisible de los equipos que fueran montados sobre la bandeja, para que la temperatura de esta no supere los 75 ºC.

Depende de en qué cara se instalen, y a qué distancia del borde. Si se instalan centrados en la cara en contacto con la batería, el problema se resolvería simplemente poniendo TB=75 ºC y calculando el flujo total de calor como antes:

>	eqTBm:=TB=Tm;'Tm'=subs(dat,Tm);Qm:=(TB-Tb)/R12;Qm_:=subs(eqR12_,eqTBm,dat,Qm);Qmload_:=Qm_-subs(dat,W);

	(2)

i.e. encima de la batería se podrían colocar equipos que disiparan 3,3 W adicionales. Podría parecer más conveniente instalar los equipos sobre la cara opuesta, que está más fría, pero depende de la distancia al borde; para una carga central sería peor:

>	QmAis:=kpC*Ly*LzC*(Tm-Tb)/(Lx/2);QmAis_:=subs(dat,%);

	(3)

i.e. en la cara opuesta a la batería, una carga central de 1,54 W ya elevaría la temperatura hasta 75 ºC, mientras que la de la batería admitiría 3,3 W como ya se ha visto (además del 1 W de la batería) debido a que el material de la batería ayuda a la conducción de calor.

c) Resolver analíticamente el problema de conducción unidimensional estacionaria con los 1 W distribuidos uniformemente sobre toda la cara del módulo.

>

eqBElocal:=rho*Ly*Lz*dx*c*diff(T(x,t),t)=W*dx/Lx+k*Ly*Lz*dx*diff(T(x,t),x,x);eqBElocal_:=0=phi+k*diff(T(x),x,x);eqT:=T=A*x+B-(phi/(2*k))*x^2;eqphi:=phi=Wst/(Lx*Ly*Lz);eqBC0:=Tb=B;eqBC1:=Tmax=subs(x=Lx,rhs(eqT));eqB0p:=k*Ly*Lz*(dT/dx)[x=0]=W;eqT_:=T=Tb+x*W/(k*Ly*Lz)-x^2*W/(2*k*Lx*Ly*Lz);eqT0:=subs(k=kpC,Lz=LzC,%);Tmax:=subs(x=Lx,rhs(%));Tmax_:=subs(dat,%);'Tmax_'=TKC(%);eq0:=diff(T(x),x)[x=0]=subs(x=0,diff(rhs(eqT0),x));eq0_:=subs(dat,%);WTm:=solve(Tm=Tmax,W);WTm_:=subs(dat,%);WTmload:='WTm-W';WTm_:=subs(dat,WTm_-W);plot(subs(dat,SI0,rhs(eqT0)),x=0..subs(dat,SI0,Lx),T=300..350);

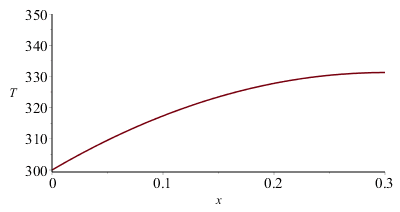i.e. si solo transmitiese la capa de CFRP, y la disipación de 1 W estuviese uniformemente distribuida, se alcanzaría una temperatura máxima de 331 K en lugar de los 311 K calculados arriba.

d) Resolver analíticamente el problema de conducción unidimensional estacionaria, pero ahora con la disipación de energía distribuida uniformemente sólo en la dirección transversal del módulo (los 80 mm).

Basta resolver dos tramos, el de la batería, y el más cercano al borde isotermo, ya que el extremo con borde adiabático quedará a temperatura uniformo.

Sea Ti la temperatura intermedia (en la interfaz entre ambos tramos).

>

eqT1:=T1(x)=Tb+(Ti-Tb)*(x/Li);eqLi:=Li=Lx/2-LxB/2;eqLi_:=subs(dat,%);eqQi:=-kpC*(Ti-Tb)/Li=-kpC*diff(T2(x),x)[x=Li];deq2:=0=diff(T2(x),x,x)+W/(LxB*Ly*LzC*kpC);dsol_:=dsolve([deq2,T2(Li)=Ti,D(T2)(Li+LxB)=0],T2(x));eqTi:=T1[x=Li]=T2[x=Li];eqQi_:=Ti=solve(lhs(eqQi)=subs(x=Li,-kpC*diff(subs(dsol_,T2(x)),x)),Ti);eqQi__:=subs(eqLi_,dat,%);Tmax2:=subs(Tb=Ti,Lx=LxB,Tmax);Tmax2_:=subs(eqQi__,dat,%);T12:=piecewise(x<Li,T1(x),x>(Li+LxB),'Tmax2',T2(x));T12_:=piecewise(x<rhs(eqLi_)/m_,subs(eqLi_,eqQi__,dat,SI0,rhs(eqT1)),x>(rhs(eqLi_)+subs(dat,LxB))/m_,Tmax2_/K_,subs(eqLi_,eqQi__,datC,dat,SI0,rhs(dsol_)));pl0_:=plot({T12_,[[rhs(eqLi_)/m_,0],[rhs(eqLi_)/m_,500],[(rhs(eqLi_)+subs(dat,LxB))/m_,500],[(rhs(eqLi_)+subs(dat,LxB))/m_,0]],[[rhs(eqLi_)/m_,0],[rhs(eqLi_)/m_,500],[(rhs(eqLi_)+subs(dat,LxB))/m_,500],[(rhs(eqLi_)+subs(dat,LxB))/m_,0]],subs(dat,SI0,rhs(eqT0))},x=0..subs(dat,SI0,Lx),T=300..350):pl0_;

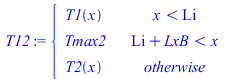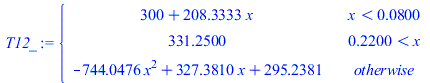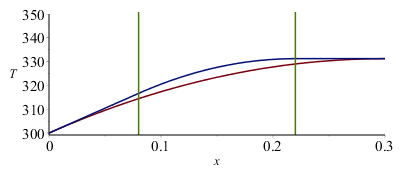i.e. todas las distribuciones longitudinales centradas dan la misma temperatura máxima (331 K para conducción solo en la capa de CFRP), y obviamente, la misma pendiente en el origen (por el que ha de salir siempre 1 W). Si se superpone a la figura anterior el perfil para 1 W centrado en 150 mm, y el de 1 W "acercado" hasta los 80 mm del borde por la gran conductividad del material de la batería, tenemos:

>

eqT150:=Tm150=Tb+W*(Lx/2)/(kpC*Ly*LzC);eqT80:=Tm80=Tb+W*Li/(kpC*Ly*LzC);subs(eqLi_,dat,[eqT150,eqT80]);Tx150:=subs(eqT150,dat,SI0,piecewise(x<Lx/2,Tb+(Tm150-Tb)*x/(Lx/2),Tm150));pl1_:=plot(Tx150,x=0..subs(dat,SI0,Lx),T=300..350):Tx80:=subs(eqT80,eqLi_,dat,SI0,piecewise(x<Li,Tb+(Tm80-Tb)*x/Li,Tm80));pl2_:=plot(Tx80,x=0..subs(dat,SI0,Lx),T=300..350):display([pl0_,pl1_,pl2_]);

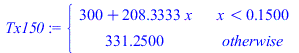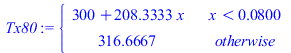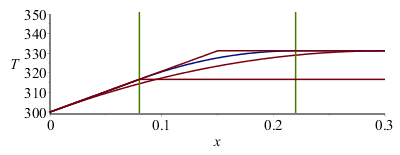donde se ve que la pendiente en el origen es siempre la misma, la Tmax para cargas centradas también (331 K), pero si la carga se acerca al borde enfriado la Tmax baja (a 317 K en este caso).

e) Resolver analíticamente el problema de conducción unidimensional estacionaria a lo largo de la capa de CFRP contabilizando también la conducción en la batería (pero no a través de la espuma).

El problema se resuelve como en el caso anterior, pero cambiando la conductividad en el tramo con batería a un valor efectivo, kef, que, si lo referimos a la misma sección de paso será kef=kC+kFLzF/LzC=30+35•6/2=135 W/(m•K).

>

eqkeff:=keff=kpC+kpB*LzB/LzC;eqT1:=T1(x)=Tb+(Ti-Tb)*(x/Li);eqLi:=Li=Lx/2-LxB/2;eqLi_:=subs(dat,%);eqQi:=-kpC*(Ti-Tb)/Li=-keff*diff(T2(x),x)[x=Li];deq2:=0=diff(T2(x),x,x)+W/(LxB*Ly*LzC*keff);dsol_:=dsolve([deq2,T2(Li)=Ti,D(T2)(Li+LxB)=0],T2(x));eqTi:=T1[x=Li]=T2[x=Li];eqQi_:=Ti=solve(lhs(eqQi)=subs(x=Li,-keff*diff(subs(dsol_,T2(x)),x)),Ti);eqQi__:=subs(eqkeff,eqLi_,dat,%);Tmax2__:=subs(kpC=keff,eqkeff,Tmax2);Tmax2_:=subs(eqQi__,dat,%);T12:=piecewise(x<Li,T1(x),x>(Li+LxB),'Tmax2',T2(x));T12_:=piecewise(x<rhs(eqLi_)/m_,subs(eqLi_,eqQi__,dat,SI0,rhs(eqT1)),x>(rhs(eqLi_)+subs(dat,LxB))/m_,Tmax2_/K_,subs(eqkeff,eqLi_,eqQi__,datC,dat,SI0,rhs(dsol_)));plot({T12_,[[rhs(eqLi_)/m_,0],[rhs(eqLi_)/m_,500],[(rhs(eqLi_)+subs(dat,LxB))/m_,500],[(rhs(eqLi_)+subs(dat,LxB))/m_,0]],[[rhs(eqLi_)/m_,0],[rhs(eqLi_)/m_,500],[(rhs(eqLi_)+subs(dat,LxB))/m_,500],[(rhs(eqLi_)+subs(dat,LxB))/m_,0]]},x=0..subs(dat,SI0,Lx),T=300..350);

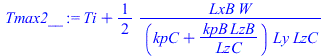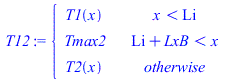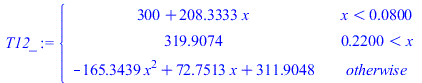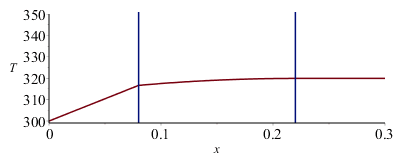i.e. la Ti sigue siendo 317 ºC, pero la máxima es 320 K en vez de 331 K.