>	restart:#"m11_p66"

Se va a estudiar la transmisión de calor a través de las paredes laterales de un cilindro de un motor de combustión. El interior está expuesto a los gases de combustión, cuya temperatura media es de 1200 K con una oscilación de 500 K (se trata de un pequeño motor de dos tiempos a 1800 rpm), con los cuales se estima que el coeficiente convectivo es de 1000 W/(m2•K), incluyendo la radiación. El exterior está en contacto con el agua de refrigeración, que está a 80 ºC y cuyo coeficiente convectivo se estima en 5000 W/(m2•K). El cilindro es de fundición de hierro de 4 mm de espesor. Se pide:
a) Hacer un esquema del perfil de temperatura esperado a través de la pared del cilindro.
b) Calcular el perfil medio de temperatura en la pared del cilindro (i.e. supuesto estacionario).
c) Calcular el flujo de calor por unidad de superficie en el caso anterior.
d) Sabiendo que la temperatura a través de la pared es de la forma T(x,t)=T0+T0exp(x/)sin(2t/x/), determinar la profundidad a la que penetran las oscilaciones térmicas en la pared, , en función del periodo,, obligando a que se cumpla la ecuación del calor.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su:="Hierro_fundido":dat:=[T1inf=1200*K_,DT1inf=500*K_,tau=1/((1800/60)/s_),h1=1000*W_/(m_^2*K_),T2inf=(80+273)*K_,h2=5000*W_/(m_^2*K_),L=0.004*m_];eqT:=T(x,t)=T0+DT0*exp(-x/xi)*sin(2*Pi*t/tau-x/xi);

Eqs. const.:

>	dat:=op(dat),get_sol_data(su),Const,SI2,SI1:a_:=subs(dat,k/(rho*c));

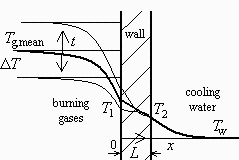
a) Hacer un esquema del perfil de temperatura esperado a través de la pared del cilindro.

/Ver figura.)
b) Calcular el perfil medio de temperatura en la pared del cilindro (i.e. supuesto estacionario).

Los balances energéticos interfaciales en cada cara son:

>	eq1:=h1*(T1inf-T1)=k*(T1-T2)/L;eq2:=k*(T1-T2)/L=h2*(T2-T2inf);sol:=solve({eq1,eq2},{T1,T2});sol_:=subs(dat,%);

c) Calcular el flujo de calor por unidad de superficie en el caso anterior.

>	eq1_:=q1=subs(sol_,dat,rhs(eq1));

d) Sabiendo que la temperatura a través de la pared es de la forma T(x,t)=T0+T0exp(x/)sin(2t/x/), determinar la profundidad a la que penetran las oscilaciones térmicas en la pared, , en función del periodo,, obligando a que se cumpla la ecuación del calor.

>	eqC:=a*diff(T(x,t),x,x)-diff(T(x,t),t)=0;eqT;eqC_:=collect(eval(subs(eqT,eqC)),[DT0,cos]);xi_:=solve(%,xi);xi=evalf(subs(a=a_,dat,%[2]));

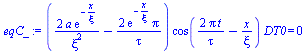i.e. para que se cumpla la ecuación del calor, ha de ser xi=sqrt(a*tau/Pi)=0,4 mm.