>	restart:#"m11_p57"

Con el fin de medir la conductividad térmica k de un material, se toma una muestra cilíndrica de 3 cm de diámetro y 10 cm de longitud, dentro de una funda lateral de aluminio de 1 mm de espesor, con bases aislantes, y se dispone en el eje un elemento calefactor de 2 mm de diámetro en el que se disipan 20 W/m. Sabiendo que en el elemento calefactor se alcanzan 50 ºC cuando el conjunto está en régimen estacionario en un ambiente a 15 ºC, se pide:
a) Hacer un esquema del perfil de temperatura esperado.
b) Plantear los balances energéticos para dos elementos interfaciales, uno a cada lado de la muestra.
c) Valor de k suponiendo un coeficiente convectivo con el aire ambiente de 10 W/(m2•K) o de 20 W/(m2•K).
d) Valor de k suponiendo que el ambiente es agua con un coeficiente de 200 W/(m2•K) o de 500 W/(m2•K).
e) Estimar el tiempo que se tardaría en alcanzar el régimen estacionario.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="Aluminio_anodizado":su2:="Arena":dat:=[D=0.03*m_,L=0.1*m_,L_Al=0.001*m_,Dcal=0.002*m_,Q_L=20*W_/m_,T1=(50+273.15)*K_,Tinf=(15+273.15)*K_,ha1=10*W_/(m_^2*K_),ha2=20*W_/(m_^2*K_),hw1=200*W_/(m_^2*K_),hw2=500*W_/(m_^2*K_)];

Eqs. const.:

>	dat:=op(dat),Const,SI2,SI1:S1dat:=get_sol_data(su1);S2dat:=get_sol_data(su2);

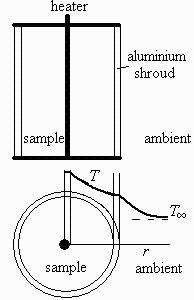
a) Hacer un esquema del perfil de temperatura esperado.

Se puede suponer que el problema es unidimensional. El perfil en la región del calefactor y en la del aluminio será casi horizontal.
Ver arriba.

b) Plantear los balances energéticos para dos elementos interfaciales, uno a cada lado de la muestra.

Como su masa es despreciable (espesor infinitesimal centrado en la interfase), no habrá acumulación, sólo flujos. Se puede hacer para toda el area Pi*D*L, por unidad de longitud axial Pi*D, o por unidad de superficie interfacial. Si lo hacemos globalmente:

>	eq0:=Q=Q_L*L;eq1:=Q=-k*Pi*Dcal*L*Diff(T,r)[r=Dcal/2];eq2:=-k*Pi*D*L*Diff(T,r)[r=D/2]=-kAl*Pi*D*L*Diff(TAl,r)[r=D/2];

que enseña que los flujos de calor a cada lado de cada interfase son iguales (para cada interfase; para todas en régimen estacionario). Nótese que, por unidad de área, el flujo no se conserva de una interfase a otra.

c) Valor de k suponiendo un coeficiente convectivo con el aire ambiente de 10 W/(m2•K) y de 20 W/(m2•K).

El efecto de la funda de aluminio será despreciable por su alta conductividad, pero lo retenemos para poder comparar.

>

eqDif:=(1/r)*diff(r*diff(T(r),r),r)=0;eqT:=dsolve(%,T(r));eqQ:=Q=2*Pi*r*L*k*Diff(T,r);eq11_7_2[1];eq1:=Q=2*k*Pi*L*(T1-T2)/ln(D/Dcal);eq2:=Q=2*kAl*Pi*L*(T2-T3)/ln((D+L_Al)/D);eq3:=Q=Pi*(D+2*L_Al)*L*h*(T3-Tinf);eq0123:=Q=(T1-Tinf)/(ln(D/Dcal)/(2*k*Pi*L)+ln((D+L_Al)/D)/(2*kAl*Pi*L)+1/(Pi*(D+2*L_Al)*L*h));ksample:=solve(%,k):ksample_air10:=evalf(subs(eq0,kAl=k,S1dat,h=ha1,dat,ksample));ksample_air10_0:=evalf(subs(eq0,L_Al=0,S1dat,h=ha1,dat,ksample));ksample_air20:=evalf(subs(eq0,kAl=k,S1dat,h=ha2,dat,ksample));

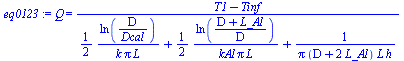i.e. con haire=10 W/(m2·K) la muestra tendría una k=0,57 W/(m·K), y hubiésemos obtenido k=0,63 W/(m·K) despreciando totalmente el efecto de la funda. La apreciable diferencia no es debida a la coductividad, sino al aumento del área, DA/A=2*L_Al/D=2*2/30=11%. Si haire=20 W/(m2·K) la muestra tendría una k=0,34 W/(m·K). Como se ve, al ser fundamental la resistencia térmica con el ambiente, es preciso conocer el coeficiente convectivo con precisión.

d) Valor de k suponiendo que el ambiente es agua con un coeficiente de 200 W/(m2•K) o de 500 W/(m2•K).

Aquí no sólo se puede despreciar el efecto de la funda sino también el del coeficiente convectivo, que puede suponerse infinito.

>	ksample_water1:=evalf(subs(eq0,kAl=k,S1dat,h=hw1,dat,ksample));ksample_water1_0:=evalf(subs(eq0,L_Al=0,S1dat,h=1e9*hw1,dat,ksample));ksample_water2:=evalf(subs(eq0,kAl=k,S1dat,h=hw2,dat,ksample));

i.e. la resistencia térmica con el ambiente es ahora despreciable y no es necesario medirla.

Comparando con el caso del aire, como la resistencia térmica es la misma, y es de la forma ln()/k+1/h, si h aumenta, la k ha de disminuir.

e) Estimar el tiempo que se tardaría en alcanzar el régimen estacionario.

Una primera estimación sería considerar el calentamiento de la muestra hasta una temperatura representativa, sin considerar las pérdidas. Podemos pensar que se calienta hasta la temperatura del calefactor, pues, aunque la media sería menor, se compensaría con las pérdidas al exterior.

>	eqHeating:=Q/L=rho*(Pi*D^2/4)*c*Diff(T,t)+ha*Pi*D*(T-Tinf);tHeating:=rho*(Pi*D^2/4)*c*(T1-Tinf)*L/Q;tHeating_:=evalf(subs(eq0,S2dat,dat,%));